莫比乌斯入门--HYSBZ - 2818

   给定一个整数n，求1<=x,y<=N且Gcd(x,y)为素数的

数对(x,y)有多少对.

  首先我们可以设 f(d) 为 d=gcd(x,y) 满足的对数。

  设 F(d) 为 d|gcd(x,y) 满足的对数。

可知，x,y,都要能被d整除，所以有： F(d)=⌊nd⌋∗⌊nd⌋

根据莫比乌斯反演公式可知： f(x)=∑x|dμ(dx)F(d)

由于 Gcd(x,y)为素数，所以： ans=∑p∑p|dμ(dp)F(d)

所以： ans=∑d⌊nd⌋∗⌊nd⌋∗∑p|dμ(dp)

所以我们需要预处理 ∑p|dμ(dp) ，设 sum(d)=∑p|dμ(dp)

由于 对任意正整数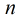有

  

                           

μ(d

所以

当 p|d p能整除d时： sum(d∗p)=μ(d) 。
当 p 不能整除 d 时： sum(d∗p)=μ(d)−sum(d)

代码如下：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <bitset>
#define siz 10000005

using namespace std;
typedef long long LL;
int prime[siz],mu[siz],sum[siz];
bool check[siz];
int n;
void Mobius(){
    mu[1] = 1;
    prime[0] = 0;
    for(int i=2;i<siz;i++){
        if(!check[i]){
            mu[i] = -1;
            sum[i] = 1;
            prime[++prime[0]] = i;
        }
        for(int j=1;j<=prime[0];j++){
            if(i*prime[j] >= siz) break;
            check[i*prime[j]] = true;
            if(i%prime[j]){
                mu[i*prime[j]] = -mu[i];
                sum[i*prime[j]] = mu[i] - sum[i];
            }
            else{
                mu[i*prime[j]] = 0;
                sum[i*prime[j]] = mu[i];
                break;
            }
        }
    }
}
void Solve(int n)
{
    LL ans = 0;
    for(int i=1;i<=n;i++){
        ans += 1LL*(n/i)*(n/i)*sum[i];
    }
    printf("%lld\n",ans);
}

int main()
{
    Mobius();
    scanf("%d",&n);
    Solve(n);
    return 0;
}