http://blog.csdn.net/shenxiaolu1984/article/details/52511202
转自:http://blog.csdn.net/majinlei121/article/details/47260917
那篇优化算法论文On optimization methods for deep learning的总结http://www.tuicool.com/articles/ZJR7Zb

总结一下,
a) 如果 f(x) 是一个标量函数,那么雅克比矩阵是一个向量,等于 f(x) 的梯度, Hesse 矩阵是一个二维矩阵。如果 f(x) 是一个向量值函数,那么Jacobi 矩阵是一个二维矩阵,Hesse 矩阵是一个三维矩阵。
b) 梯度是 Jacobian 矩阵的特例,梯度的 jacobian 矩阵就是 Hesse 矩阵(一阶偏导与二阶偏导的关系)。
3. 优化方法
1) Gradient Descent
Gradient descent 又叫 steepest descent,是利用一阶的梯度信息找到函数局部最优解的一种方法,也是机器学习里面最简单最常用的一种优化方法。Gradient descent 是 line search 方法中的一种,主要迭代公式如下:
其中,是第 k 次迭代我们选择移动的方向,在 steepest descent 中,移动的方向设定为梯度的负方向,
是第 k 次迭代用 line search 方法选择移动的距离,每次移动的距离系数可以相同,也可以不同,有时候我们也叫学习率(learning rate)。
在数学上,移动的距离可以通过 line search 令导数为零找到该方向上的最小值,但是在实际编程的过程中,这样计算的代价太大,我们一般可以将它设定位一个常量。考虑一个包含三个变量的函数,计算梯度得到
。设定 learning rate = 1,算法代码如下:
# Code from Chapter 11 of Machine Learning: An Algorithmic Perspective# by Stephen Marsland (http://seat.massey.ac.nz/personal/s.r.marsland/MLBook.html)# Gradient Descent using steepest descentfrom numpy import *def Jacobian(x): return array([x[0], 0.4*x[1], 1.2*x[2]])def steepest(x0): i = 0 iMax = 10 x = x0 Delta = 1 alpha = 1 while i<iMax and Delta>10**(-5): p = -Jacobian(x) xOld = x x = x + alpha*p Delta = sum((x-xOld)**2) print 'epoch', i, ':' print x, '\n' i += 1x0 = array([-2,2,-2])steepest(x0)
Steepest gradient 方法得到的是局部最优解,如果目标函数是一个凸优化问题,那么局部最优解就是全局最优解,理想的优化效果如下图,值得注意一点的是,每一次迭代的移动方向都与出发点的等高线垂直:

需要指出的是,在某些情况下,最速下降法存在锯齿现象( zig-zagging)将会导致收敛速度变慢:
粗略来讲,在二次函数中,椭球面的形状受 hesse 矩阵的条件数影响,长轴与短轴对应矩阵的最小特征值和最大特征值的方向,其大小与特征值的平方根成反比,最大特征值与最小特征值相差越大,椭球面越扁,那么优化路径需要走很大的弯路,计算效率很低。
2) Newton’s method
在最速下降法中,我们看到,该方法主要利用的是目标函数的局部性质,具有一定的“盲目性”。牛顿法则是利用局部的一阶和二阶偏导信息,推测整个目标函数的形状,进而可以求得出近似函数的全局最小值,然后将当前的最小值设定近似函数的最小值。相比最速下降法,牛顿法带有一定对全局的预测性,收敛性质也更优良。牛顿法的主要推导过程如下:
第一步,利用 Taylor 级数求得原目标函数的二阶近似:
第二步,把 x 看做自变量, 所有带有 x^k 的项看做常量,令一阶导数为 0 ,即可求近似函数的最小值:即:第三步,将当前的最小值设定近似函数的最小值(或者乘以步长)。
与 1) 中优化问题相同,牛顿法的代码如下:
Newton.py
# Code from Chapter 11 of Machine Learning: An Algorithmic Perspective# by Stephen Marsland (http://seat.massey.ac.nz/personal/s.r.marsland/MLBook.html)# Gradient Descent using Newton's methodfrom numpy import *def Jacobian(x): return array([x[0], 0.4*x[1], 1.2*x[2]])def Hessian(x): return array([[1,0,0],[0,0.4,0],[0,0,1.2]])def Newton(x0): i = 0 iMax = 10 x = x0 Delta = 1 alpha = 1 while i<iMax and Delta>10**(-5): p = -dot(linalg.inv(Hessian(x)),Jacobian(x)) xOld = x x = x + alpha*p Delta = sum((x-xOld)**2) i += 1 print x x0 = array([-2,2,-2])Newton(x0)
上面例子中由于目标函数是二次凸函数,Taylor 展开等于原函数,所以能一次就求出最优解。
牛顿法主要存在的问题是:
Hesse 矩阵不可逆时无法计算
矩阵的逆计算复杂为 n 的立方,当问题规模比较大时,计算量很大,解决的办法是采用拟牛顿法如 BFGS, L-BFGS, DFP, Broyden’s Algorithm 进行近似。
如果初始值离局部极小值太远,Taylor 展开并不能对原函数进行良好的近似
3) Levenberg–Marquardt Algorithm
Levenberg–Marquardt algorithm 能结合以上两种优化方法的优点,并对两者的不足做出改进。与 line search 的方法不同,LMA 属于一种“信赖域法”(trust region),牛顿法实际上也可以看做一种信赖域法,即利用局部信息对函数进行建模近似,求取局部最小值。所谓的信赖域法,就是从初始点开始,先假设一个可以信赖的最大位移 s(牛顿法里面 s 为无穷大),然后在以当前点为中心,以 s 为半径的区域内,通过寻找目标函数的一个近似函数(二次的)的最优点,来求解得到真正的位移。在得到了位移之后,再计算目标函数值,如果其使目标函数值的下降满足了一定条件,那么就说明这个位移是可靠的,则继续按此规则迭代计算下去;如果其不能使目标函数值的下降满足一定的条件,则应减小信赖域的范围,再重新求解。
LMA 最早提出是用来解决最小二乘法曲线拟合的优化问题的,对于随机初始化的已知参数 beta, 求得的目标值为:

对拟合曲线函数进行一阶 Jacobi 矩阵的近似:进而推测出 S 函数的周边信息:位移是多少时得到 S 函数的最小值呢?通过几何的概念,当残差垂直于 J 矩阵的 span 空间时, S 取得最小(至于为什么?请参考之前博客的最后一部分)我们将这个公式略加修改,加入阻尼系数得到:就是莱文贝格-马夸特方法。这种方法只计算了一阶偏导,而且不是目标函数的 Jacobia 矩阵,而是拟合函数的 Jacobia 矩阵。当
大的时候可信域小,这种算法会接近最速下降法,
小的时候可信域大,会接近高斯-牛顿方法。




算法过程如下:
给定一个初识值 x0
当
并且没有到达最大迭代次数时
重复执行:
算出移动向量
计算更新值:
计算目标函数真实减少量与预测减少量的比率
if
,接受更新值
else if
,说明近似效果很好,接受更新值,扩大可信域(即减小阻尼系数)
else: 目标函数在变大,拒绝更新值,减小可信域(即增加阻尼系数)
直到达到最大迭代次数
维基百科在介绍 Gradient descent 时用包含了细长峡谷的 Rosenbrock function

展示了 zig-zagging 锯齿现象:用 LMA 优化效率如何。套用到我们之前 LMA 公式中,有:代码如下:

LevenbergMarquardt.py
# Code from Chapter 11 of Machine Learning: An Algorithmic Perspective# by Stephen Marsland (http://seat.massey.ac.nz/personal/s.r.marsland/MLBook.html)# The Levenberg Marquardt algorithmfrom numpy import *def function(p): r = array([10*(p[1]-p[0]**2),(1-p[0])]) fp = dot(transpose(r),r) #= 100*(p[1]-p[0]**2)**2 + (1-p[0])**2 J = (array([[-20*p[0],10],[-1,0]])) grad = dot(transpose(J),transpose(r)) return fp,r,grad,Jdef lm(p0,tol=10**(-5),maxits=100): nvars=shape(p0)[0] nu=0.01 p = p0 fp,r,grad,J = function(p) e = sum(dot(transpose(r),r)) nits = 0 while nits<maxits and linalg.norm(grad)>tol: nits += 1 fp,r,grad,J = function(p) H=dot(transpose(J),J) + nu*eye(nvars) pnew = zeros(shape(p)) nits2 = 0 while (p!=pnew).all() and nits2<maxits: nits2 += 1 dp,resid,rank,s = linalg.lstsq(H,grad) pnew = p - dp fpnew,rnew,gradnew,Jnew = function(pnew) enew = sum(dot(transpose(rnew),rnew)) rho = linalg.norm(dot(transpose(r),r)-dot(transpose(rnew),rnew)) rho /= linalg.norm(dot(transpose(grad),pnew-p)) if rho>0: update = 1 p = pnew e = enew if rho>0.25: nu=nu/10 else: nu=nu*10 update = 0 print fp, p, e, linalg.norm(grad), nup0 = array([-1.92,2])lm(p0)
大概 5 次迭代就可以得到最优解 (1, 1).
Levenberg–Marquardt algorithm 对局部极小值很敏感,维基百科举了一个二乘法曲线拟合的例子,当使用不同的初始值时,得到的结果差距很大,我这里也有Python 代码,就不细说了。
4) Conjugate Gradients
共轭梯度法也是优化模型经常经常要用到的一个方法,背后的数学公式和原理稍微复杂一些,光这一个优化方法就可以写一篇很长的博文了,所以这里并不打算详细讲解每一步的推导过程,只简单写一下算法的实现过程。与最速梯度下降的不同,共轭梯度的优点主要体现在选择搜索方向上。在了解共轭梯度法之前,我们首先简单了解一下共轭方向:

共轭方向和马氏距离的定义有类似之处,他们都考虑了全局的数据分布。如上图,d(1) 方向与二次函数的等值线相切,d(1) 的共轭方向 d(2) 则指向椭圆的中心。所以对于二维的二次函数,如果在两个共轭方向上进行一维搜索,经过两次迭代必然达到最小点。前面我们说过,等值线椭圆的形状由 Hesse 矩阵决定,那么,上图的两个方向关于 Hessen 矩阵正交,共轭方向的定义如下:如果椭圆是一个正圆, Hessen 矩阵是一个单位矩阵,上面等价于欧几里得空间中的正交。
在优化过程中,如果我们确定了移动方向(GD:垂直于等值线,CG:共轭方向),然后在该方向上搜索极小值点(恰好与该处的等值线相切),然后移动到最小值点,重复以上过程,那么 Gradient Descent 和 Conjugate gradient descent 的优化过程可以用下图的绿线与红线表示:

讲了这么多,共轭梯度算法究竟是如何算的呢?
给定一个出发点 x0 和一个停止参数 e, 第一次移动方向为最速下降方向:
while
:
用 Newton-Raphson 迭代计算移动距离,以便在该搜索方向移动到极小,公式就不写了,具体思路就是利用一阶梯度的信息向极小值点跳跃搜索
移动当前的优化解 x:
用 Gram-Schmidt 方法构造下一个共轭方向,即
, 按照
的确定公式又可以分为 FR 方法和 PR 和 HS 等。
在很多的资料中,介绍共轭梯度法都举了一个求线性方程组 Ax = b 近似解的例子,实际上就相当于这里所说的
还是用最开始的目标函数 来编写共轭梯度法的优化代码:
# Code from Chapter 11 of Machine Learning: An Algorithmic Perspective# by Stephen Marsland (http://seat.massey.ac.nz/personal/s.r.marsland/MLBook.html)# The conjugate gradients algorithmfrom numpy import *def Jacobian(x): #return array([.4*x[0],2*x[1]]) return array([x[0], 0.4*x[1], 1.2*x[2]])def Hessian(x): #return array([[.2,0],[0,1]]) return array([[1,0,0],[0,0.4,0],[0,0,1.2]])def CG(x0): i=0 k=0 r = -Jacobian(x0) p=r betaTop = dot(r.transpose(),r) beta0 = betaTop iMax = 3 epsilon = 10**(-2) jMax = 5 # Restart every nDim iterations nRestart = shape(x0)[0] x = x0 while i < iMax and betaTop > epsilon**2*beta0: j=0 dp = dot(p.transpose(),p) alpha = (epsilon+1)**2 # Newton-Raphson iteration while j < jMax and alpha**2 * dp > epsilon**2: # Line search alpha = -dot(Jacobian(x).transpose(),p) / (dot(p.transpose(),dot(Hessian(x),p))) print "N-R",x, alpha, p x = x + alpha * p j += 1 print x # Now construct beta r = -Jacobian(x) print "r: ", r betaBottom = betaTop betaTop = dot(r.transpose(),r) beta = betaTop/betaBottom print "Beta: ",beta # Update the estimate p = r + beta*p print "p: ",p print "----" k += 1 if k==nRestart or dot(r.transpose(),p) <= 0: p = r k = 0 print "Restarting" i +=1 print xx0 = array([-2,2,-2])CG(x0)
转自:http://www.cnblogs.com/joneswood/archive/2012/03/11/2390529.html
牛顿法中,在每一次要得到新的搜索方向的时候,都需要计算Hessian矩阵(二阶导数矩阵)。在自变量维数非常大的时候,这个计算工作是非常耗时的,因此,拟牛顿法的诞生的意义就是:它采用了一定的方法来构造与Hessian矩阵相似的正定矩阵,而这个构造方法计算量比牛顿法小。
a. DFP算法
假设目标函数可以用二次函数进行近似(实际上很多函数可以用二次函数很好地近似):
忽略高阶无穷小部分,只看前面3项,其中A为目标函数的Hessian矩阵。此式等号两边对X求导,可得:
于是,当 X=Xi 时,将[2]式两边均左乘Ai+1-1,有:
上式左右两边近似相等,但如果我们把它换成等号,并且用另一个矩阵H来代替上式中的A-1,则得到:
方程[4]就是拟牛顿方程,其中的矩阵H,就是Hessian矩阵的逆矩阵的一个近似矩阵.在迭代过程中生成的矩阵序列H0,H1,H2,……中,每一个矩阵Hi+1,都是由前一个矩阵Hi修正得到的。DFP算法的修正方法如下,设:
再设:
其中,m和n均为实数,v和w均为N维向量。将[6]代入[5]式,再将[5]式代入[4]式,可得:
得到的m,n,v,w值如下:
将[8]~[11]代入[6]式,然后再将[6]代入[5]式,就得到了Hessian矩阵的逆矩阵的近似阵H的计算方法:
通过上述描述,DFP算法的流程大致如下:
已知初始正定矩阵H0,从一个初始点开始(迭代),用式子 ![]() 来计算出下一个搜索方向,并在该方向上求出可使目标函数极小化的步长α,然后用这个步长,将当前点挪到下一个点上,并检测是否达到了程序终止的条件,如果没有达到,则用上面所说的[13]式的方法计算出下一个修正矩阵H,并计算下一个搜索方向……周而复始,直到达到程序终止条件。
来计算出下一个搜索方向,并在该方向上求出可使目标函数极小化的步长α,然后用这个步长,将当前点挪到下一个点上,并检测是否达到了程序终止的条件,如果没有达到,则用上面所说的[13]式的方法计算出下一个修正矩阵H,并计算下一个搜索方向……周而复始,直到达到程序终止条件。
值得注意的是,矩阵H正定是使目标函数值下降的条件,所以,它保持正定性很重要。可以证明,矩阵H保持正定的充分必要条件是:
在迭代过程中,这个条件也是容易满足的。
b. BFGS算法
BFGS算法和DFP算法有些相似,但是形式上更加复杂一些。BFGS算法目前仍然被认为是最好的拟牛顿算法。BFGS算法中矩阵H的计算公式如下所示:
在[14]式中的最后一项(蓝色部分)就是BFGS比DFP多出来的部分,其中w是一个n×1的向量。
在目标函数为二次型时,无论是DFP还是BFGS——也就是说,无论[14]式中有没有最后一项——它们均可以使矩阵H在n步之内收敛于A-1。
BFGS算法有一个变种,叫作“Limited-memory BFGS”,简称“L-BFGS”。使用L-BFGS算法来编写程序时,它会比BFGS算法占用的内存小。
另外,还有“面向象限”的OWLQN算法(Orthant-Wise Limited-memoryQuai-Newton),这里不再赘述。
代码实验:
网络上面有很多BFGS的实现算法,用的比较多的是c++实现的源码库libbfgs,http://www.chokkan.org/software/liblbfgs/.
转自:http://blog.csdn.net/luo123n/article/details/48239963
前言
这里讨论的优化问题指的是,给定目标函数f(x),我们需要找到一组参数x,使得f(x)的值最小。
本文以下内容假设读者已经了解机器学习基本知识,和梯度下降的原理。
SGD
SGD指stochastic gradient descent,即随机梯度下降。是梯度下降的batch版本。
对于训练数据集,我们首先将其分成n个batch,每个batch包含m个样本。我们每次更新都利用一个batch的数据,而非整个训练集。即:
xt+1=xt+Δxt
Δxt=−ηgt
其中,η为学习率,gt为x在t时刻的梯度。
这么做的好处在于:
当训练数据太多时,利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力,并且可以更快地收敛。
当训练集有很多冗余时(类似的样本出现多次),batch方法收敛更快。以一个极端情况为例,若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch,后一半作为另一个batch,那么在一次遍历训练集时,batch的方法向最优解前进两个step,而整体的方法只前进一个step。
Momentum
SGD方法的一个缺点是,其更新方向完全依赖于当前的batch,因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入momentum。
momentum即动量,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。这样一来,可以在一定程度上增加稳定性,从而学习地更快,并且还有一定摆脱局部最优的能力:
Δxt=ρΔxt−1−ηgt
其中,ρ 即momentum,表示要在多大程度上保留原来的更新方向,这个值在0-1之间,在训练开始时,由于梯度可能会很大,所以初始值一般选为0.5;当梯度不那么大时,改为0.9。η 是学习率,即当前batch的梯度多大程度上影响最终更新方向,跟普通的SGD含义相同。ρ 与η 之和不一定为1。
Nesterov Momentum
这是对传统momentum方法的一项改进,由Ilya Sutskever(2012 unpublished)在Nesterov工作的启发下提出的。
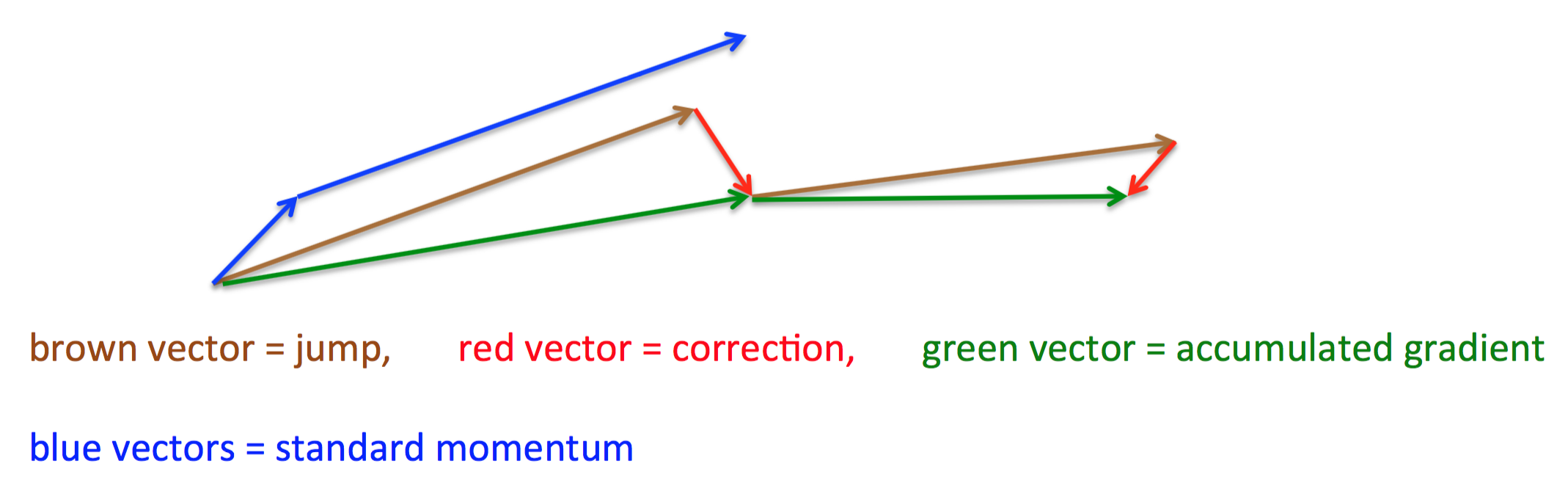
其基本思路如下图(转自Hinton的coursera公开课lecture 6a):
首先,按照原来的更新方向更新一步(棕色线),然后在该位置计算梯度值(红色线),然后用这个梯度值修正最终的更新方向(绿色线)。上图中描述了两步的更新示意图,其中蓝色线是标准momentum更新路径。
公式描述为:
Δxt=ρΔxt−1−ηΔf(xt+ρΔxt−1)
Adagrad
上面提到的方法对于所有参数都使用了同一个更新速率。但是同一个更新速率不一定适合所有参数。比如有的参数可能已经到了仅需要微调的阶段,但又有些参数由于对应样本少等原因,还需要较大幅度的调动。
Adagrad就是针对这一问题提出的,自适应地为各个参数分配不同学习率的算法。其公式如下:
Δxt=−η∑tτ=1g2τ+ϵ−−−−−−−−−−√gt
其中gt 同样是当前的梯度,连加和开根号都是元素级别的运算。eta 是初始学习率,由于之后会自动调整学习率,所以初始值就不像之前的算法那样重要了。而ϵ是一个比较小的数,用来保证分母非0。
其含义是,对于每个参数,随着其更新的总距离增多,其学习速率也随之变慢。
Adadelta
Adagrad算法存在三个问题
其学习率是单调递减的,训练后期学习率非常小
其需要手工设置一个全局的初始学习率
更新xt时,左右两边的单位不同一
Adadelta针对上述三个问题提出了比较漂亮的解决方案。
首先,针对第一个问题,我们可以只使用adagrad的分母中的累计项离当前时间点比较近的项,如下式:
E[g2]t=ρE[g2]t−1+(1−ρ)g2t
Δxt=−ηE[g2]t+ϵ−−−−−−−−√gt
这里ρ是衰减系数,通过这个衰减系数,我们令每一个时刻的gt随之时间按照ρ指数衰减,这样就相当于我们仅使用离当前时刻比较近的gt信息,从而使得还很长时间之后,参数仍然可以得到更新。
针对第三个问题,其实sgd跟momentum系列的方法也有单位不统一的问题。sgd、momentum系列方法中:
Δx的单位∝g的单位∝∂f∂x∝1x的单位
类似的,adagrad中,用于更新Δx的单位也不是x的单位,而是1。
而对于牛顿迭代法:
Δx=H−1tgt
其中H为Hessian矩阵,由于其计算量巨大,因而实际中不常使用。其单位为:
Δx∝H−1g∝∂f∂x∂2f∂2x∝x的单位
注意,这里f无单位。因而,牛顿迭代法的单位是正确的。
所以,我们可以模拟牛顿迭代法来得到正确的单位。注意到:
Δx=∂f∂x∂2f∂2x⇒1∂2f∂2x=Δx∂f∂x
这里,在解决学习率单调递减的问题的方案中,分母已经是∂f∂x的一个近似了。这里我们可以构造Δx的近似,来模拟得到H−1的近似,从而得到近似的牛顿迭代法。具体做法如下:
Δxt=−E[Δx2]t−1−−−−−−−−√E[g2]t+ϵ−−−−−−−−√gt
可以看到,如此一来adagrad中分子部分需要人工设置的初始学习率也消失了,从而顺带解决了上述的第二个问题。
各个方法的比较
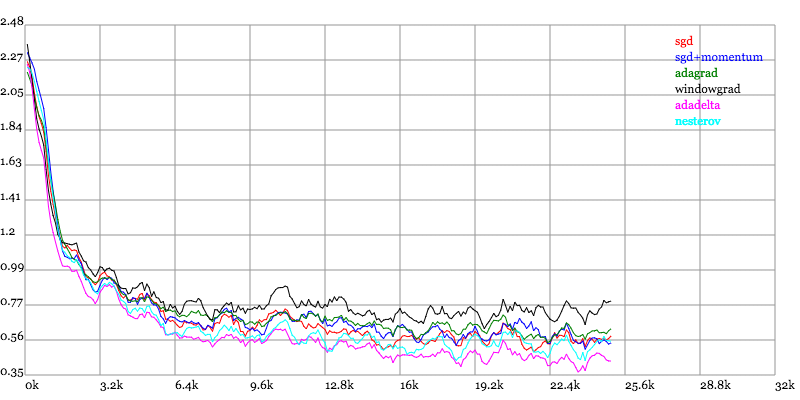
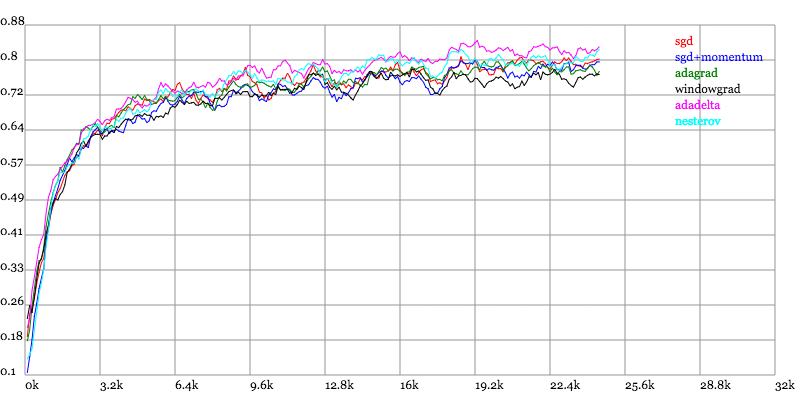
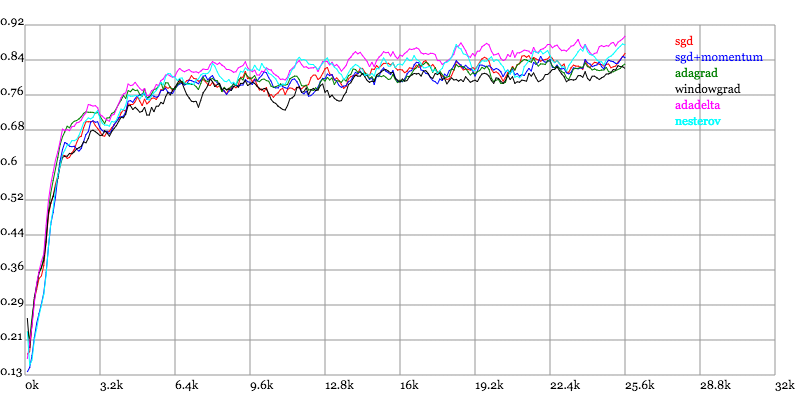
Karpathy做了一个这几个方法在MNIST上性能的比较,其结论是:
adagrad相比于sgd和momentum更加稳定,即不需要怎么调参。而精调的sgd和momentum系列方法无论是收敛速度还是precision都比adagrad要好一些。在精调参数下,一般Nesterov优于momentum优于sgd。而adagrad一方面不用怎么调参,另一方面其性能稳定优于其他方法。
实验结果图如下:
Loss vs. Number of examples seen
Testing Accuracy vs. Number of examples seen
Training Accuracy vs. Number of examples seen
其他总结文章
最近看到了一个很棒的总结文章,除了本文的几个算法,还总结了RMSProp跟ADAM(其中ADAM是目前最好的优化算法,不知道用什么的话用它就对了)
Stochastic Gradient Descent (SGD)
SGD的参数
在使用随机梯度下降(SGD)的学习方法时,一般来说有以下几个可供调节的参数:
Learning Rate 学习率
Weight Decay 权值衰减
Momentum 动量
Learning Rate Decay 学习率衰减
再此之中只有第一的参数(Learning Rate)是必须的,其余部分都是为了提高自适应性的参数,也就是说后3个参数不需要时可以设为0。
Learning Rate
学习率决定了权值更新的速度,设置得太大会使结果越过最优值,太小会使下降速度过慢。仅靠人为干预调整参数需要不断修改学习率,因此后面3种参数都是基于自适应的思路提出的解决方案。
wi←wi−η∂E∂wi
在实际运用中,为了避免模型的over-fitting,需要对cost function加入规范项,在SGD中我们加入$−ηλw_i$这一项来对cost function进行规范化。
wi←wi−η∂E∂wi−ηλwi
这个公式的基本思路是减小不重要的参数对结果的影响,而有用的权重则不会受到Weight decay的影响,这种思路与Dropout的思路原理上十分相似。
一种提高SGD寻优能力的方法,具体做法是每次迭代减小学习率的大小。
initial learning rate $\eta=\eta_0$
learning rate decay $\eta_d$
At each iteration $s$:
η(s)=η01+s⋅ηd
在许多论文中,另一种比较常见的方法是迭代30-50次左右直接对学习率进行操作($\eta←0.5\cdot\eta$)
灵感来自于牛顿第一定律,基本思路是为寻优加入了“惯性”的影响,这样一来,当误差曲面中存在平坦区SGD可以一更快的速度学习。
wi←m⋅wi−η∂E∂wi
注意:这里的表示方法并没有统一的规定,这里只是其中一种
SGD优缺点
实现简单,当训练样本足够多时优化速度非常快
需要人为调整很多参数,比如学习率,收敛准则等
Averaged Stochastic Gradient Descent (ASGD)
在SGD的基础上计算了权值的平均值。
$$\bar{w}t=\frac{1}{t-t_0}\sum^t{i=t_0+1} w_t$$
ASGD的参数
在SGD的基础上增加参数$t_0$
学习率 $\eta$
参数 $t_0$
ASGD优缺点
运算花费和second order stochastic gradient descent (2SGD)一样小。
比SGD的训练速度更为缓慢。
$t_0$的设置十分困难
3. Conjugate Gradient(共轭梯度法)
介于最速下降法与牛顿法之间的一个方法,它仅仅需要利用一阶导数的信息,克服了GD方法收敛慢的特点。
Limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) (一种拟牛顿算法)
L-BFGS算法比较适合在大规模的数值计算中,具备牛顿法收敛速度快的特点,但不需要牛顿法那样存储Hesse矩阵,因此节省了大量的空间以及计算资源。
不同的优化算法有不同的优缺点,适合不同的场合:
LBFGS算法在参数的维度比较低(一般指小于10000维)时的效果要比SGD(随机梯度下降)和CG(共轭梯度下降)效果好,特别是带有convolution的模型。
针对高维的参数问题,CG的效果要比另2种好。也就是说一般情况下,SGD的效果要差一些,这种情况在使用GPU加速时情况一样,即在GPU上使用LBFGS和CG时,优化速度明显加快,而SGD算法优化速度提高很小。
在单核处理器上,LBFGS的优势主要是利用参数之间的2阶近视特性来加速优化,而CG则得得益于参数之间的共轭信息,需要计算器Hessian矩阵。
补充一份知乎:https://zhuanlan.zhihu.com/p/22252270








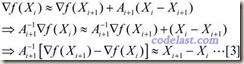
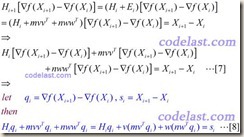

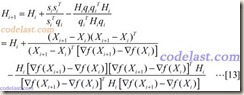
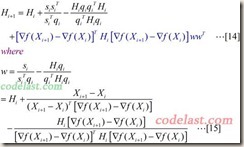













 4131
4131











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








