【树的倍增】【二分 or LCA】USACO MAR11银组 聚会地点

---

---

题目

时间限制: 1 Sec 内存限制: 64 MB

题目描述

Bessie和Jon每天都要去他们所居住的小镇的某些地方游玩。有趣的是，他们居住的小镇是一个树的结构，也就意味是，小镇的每个地方之间有且仅有一条通路（不是指一条边，而是指一条通路），每个地方都会有且仅有一个父亲地点（除了小镇的城镇中心，它没有祖先）。
小镇共有N个地点(1 <= N <= 1,000)，编号1～N。点1是镇的中心。
Bessie和Jon决定每天都要在游玩后见面，他们见面的地点总是在他们游玩的两个地方之间的那条通路中，离城镇中心最近的地方，下面给出他们的旅行日程，你需要帮他们每天的见面地点。
你可以理解为城镇中心就是成为在这个树结构上的根。

             [1]
            / | \
           /  |  \
         [2] [3] [6]
         /       / \
        /       /   \
      [4]      [8]  [9]
               / \
              /   \
            [5]   [7]

以下为他们某次见面的安排：

Bessie	Jon	Meeting Place
2	7	1
4	2	2
1	1	1
4	1	1
7	5	8
9	5	6
1	1	1

输入

第1行：两个数N,M代表一共有N个地方，B和J已经进行了M次见面
第2..N-1行，每行一个数X，代表第i个地点的父亲为X
再接下来M行，每行两个数，分别代表B和J当天准备去游玩的地方
1<=N<=1000,1<=M<=1000

输出

一共M行，每行一个数代表B和J当天见面的地方。

样例输入

9 6
1
1
2
8
1
8
6
6
2 7
4 2
3 3
4 1
7 5
9 5

样例输出

1
2
3
1
8
6

题目大意

尽管是中文，但是很长，说白了就是裸的LCA，给你一棵N个节点的树（根为1），M次询问，每次输出两个点的LCA。

LCA

LCA（Least Common Ancestors）是什么？即点的最近公共祖先。
也就是说，对于点a,b,分别按照a到根的路径和b到根的路径寻找，路径上第一个重合的点即为它们的LCA，题目中已经列了表格说明，可自行参照图看。

倍增

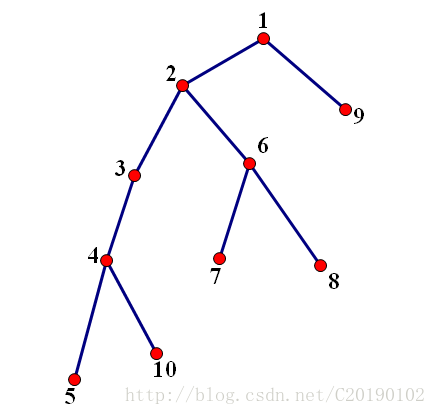
下面这棵树用来举例：

概念

我不知道耶QAQ

定义

令数组f[i][j]表示第i个结点的第$2^j$个祖先（父亲为第1个祖先，祖父为第2个祖先，以此类推），莫名想到树状数组……例如f[5][2]=1,f[8][1]=2。

预处理

方法

我们可以用$\Theta(Nlog_2N)$的时间预处理出这个数组（数组的大小也只有$N \times log_2N$）。
f数组的递推式：

$$f[i][0]=father[i]$$ $$f[i][j]=f[f[i][j-1]][j-1]$$
第一个式子不解释，第二个式子：
我们都知道 $2^{i-1}+2^{i-1}=2 \times 2^{i-1}=2^i$
所以，“i的第 $2^{i-1}$个祖先的 $2^{i-1}$个祖先”就是i的第 $2^i$个祖先。

代码

for(int i=1;i<=N;i++)
    f[i][0]=fa[i];
for(int j=1;j<=LOG;j++)
    for(int i=1;i<=N;i++)
        f[i][j]=f[f[i][j-1]][j-1];

其中LOG为一个常数，显然是取$log_2\ MAXN$，例如这道题取$log_21000\approx 10$，当然只有在一条链的情况下才会有f[i][9]。

另外，j在外层，每次调用f[i][j]和f[i][j+1]的时间间隔很久，计算机的速度会变慢，所以也可以把f[i][j]的意义变为j的第$2^i$个祖先。

操作1

概念

获取x的第k个祖先，通常称为getk操作。

方法

和二进制相关，需用到位运算，将k的二进制的每一位分离出来，对于第i位，如果为1，ans+=f[x][i]。

代码

for(int i=0;i<LOG;i++)
    if(k&(1<<i))
        x=f[x][i];
    return x;

操作2

概念

求x的深度为k的祖先，通常称为getd操作。

方法

显然，getd(x,k)=getk(x,dep[x]-k),其中dep[x]为x的深度。
dep可以在开始时用一次dfs初始化出来：

//c[i][j]表示i的第j个儿子，为vector
void dfs(int x,int s)//x为当前节点，s为当前深度
{
    int l=c[x].size();
    dep[x]=s;
    for(int i=0;i<l;i++)
        dfs(c[x][i],s+1);//儿子的深度比它多1
}
int main()
{
    dfs(1,0);//根的深度为0（或者1也行）
}

代码

int getd(int x,int k)
{
    return getk(x,dep[x]-k);
}

求LCA

纯暴力

方法

按照前面LCA的概念，我们想找5和8的LCA，分别列举它们到根的路径：
5 4 3 2 1
8 6 2 1
我们从后往前依次比对两个序列，直到找到不相同的一个，那么它的上一个就是两个点的LCA了。
1 1 same
2 2 same
3 6 different
4 8 …
5
发现第三个不同了，所以5和8的LCA就是第2行的结点，即结点2。

为什么不能从前往后找第一个相同的呢？从上面的数据就能看出，如果两个结点的深度不同，就会出问题，你在比较的时候必须比较同一深度的结点。

代码

代码很容易实现，这里就不给了(｡･ω･｡)，不要打我。

时间复杂度

容易得出$\Theta(3 \times N)$，两个结点查找路径为2N，比对N，事实上常数3可以忽略，看做$\Theta(N)$。

二分

方法

准确的说，应该是二分答案，我们二分LCA的深度。
设要求LCA的两个点是u和v(dep[u]≥dep[v]即u在)，
显然LCA(u,v)的深度不会超过dep[v]，
所以，二分的时候l=1,r=dep[v]，

怎么验证答案是否正确呢？
令t=getd(u,dep[v])即u的祖先中与v的深度相同的一个。
设当前二分的答案为mid，很简单了：若getd(t,mid)=getd(v,mid)，则mid一定符合条件，我们就应该找比mid更深的点，即l=mid+1。反之，则mid大了，r=mid-1。

代码

int BL(int u,int v)//二分真的是暴力哦
{
    if(dep[u]<dep[v]) swap(u,v);//保证dep[u]≥dep[v]
    int t=getd(u,dep[v]);
    if(t==v) return t;//注意处理同一个点的情况
    int l=1,r=dep[v];
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(getd(t,mid)==getd(v,mid)) l=mid+1;
        else r=mid-1;
    }
    return fa[getd(v,l)];//注意，二分跳出来后l和r都是不满足条件的，以l为例，l是mid+1，所以最后的答案是getd(v,l)的父亲
}

时间复杂度

二分为$\Theta(log_2N)$，每次验证为$\Theta(log_2N)$，所以总的时间复杂度就为$\Theta({log_2N}^2)$。

原汁原味的倍增

终于写到这里了，写这篇博客写了我1辈子o(▼皿▼メ;)o

方法

首先，还是要将u和v统一到深度，然后，令i从LOG开始枚举，一直到0，比较f[t][i]和f[v][i]（t同二分里面的t），如果不同，就将t=f[t][i],v=f[v][i]，为什么？我也不知道，但是就是觉得是对的= =，就这个feel。
大概讲一下我的感觉：枚举$2^i$，且从大到小，是能够精确地枚举到每个点的，所以就这样了= =。

代码

int LCA(int u,int v)
{
    if(dep[u]<dep[v]) swap(u,v);
    int t=getd(u,dep[v]);
    if(t==v) return t;
    for(int i=LOG-1;i>=0;i--)
        if(f[t][i]!=f[v][i])
            t=f[t][i],v=f[v][i];
}

时间复杂度

i从LOG到0，显然时间复杂度为$\Theta(log_2N)$，已经很快啦，当然还有$\Theta(1)$的办法，但是超级麻烦，只要用的不多，$\Theta(log_2N)$足矣。

完整代码

即这道题的代码（二分和倍增两种方法）：

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
int read()
{
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
#define MAXN 1200
#define LOG 15
int dep[MAXN+5];
int fa[MAXN+5],f[MAXN+5][LOG+5];
int N,M;

vector<int> c[MAXN+5];

void initf()
{
    for(int i=1;i<=N;i++) f[i][0]=fa[i];
    for(int j=1;j<=LOG;j++)
        for(int i=1;i<=N;i++)
            f[i][j]=f[f[i][j-1]][j-1];
}

int getk(int x,int k)
{
    for(int i=0;i<LOG;i++)
        if(k&(1<<i))
            x=f[x][i];
    return x;
}

int getd(int x,int k)
{
    return getk(x,dep[x]-k);
}

void dfs(int x,int s)
{
    int l=c[x].size();
    dep[x]=s;
    for(int i=0;i<l;i++)
        dfs(c[x][i],s+1);
}

int BL(int u,int v)
{
    if(dep[u]<dep[v]) swap(u,v);
    int t=getd(u,dep[v]);
    if(t==v) return t;
    int l=1,r=dep[v];
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(getd(t,mid)==getd(v,mid)) l=mid+1;
        else r=mid-1;
    }
    return fa[getd(v,l)];
}

int LCA(int u,int v)
{
    if(dep[u]<dep[v]) swap(u,v);
    int t=getd(u,dep[v]);
    if(t==v) return t;
    for(int i=LOG-1;i>=0;i--)
        if(f[t][i]!=f[v][i])
            t=f[t][i],v=f[v][i];
    return fa[t];
}

int main()
{
    N=read(),M=read();
    for(int i=2;i<=N;i++)
        fa[i]=read(),c[fa[i]].push_back(i);
    initf();
    dfs(1,0);
    //for(int i=1;i<=N;i++) printf("dep[%d] = %d\n",i,dep[i]);
    while(M--)
    {
        int u=read(),v=read();
        //printf("%d\n",BL(u,v));
        printf("%d\n",LCA(u,v));
    }
}