二叉树的遍历与青蛙跳台阶——利用递归的数据结构来理解递归过程

引言

     某些数据结构就是递归的，则他们的操作可递归地描述。例如，链表就是

一种递归的数据结构，链表节点Lnode的定义由数据域data和指针域next组成 ，

而指针next则由Lnode定义。

     树形结构也是以多重链表作为其存储表示的递归结构。

     所以关于链表和树的一些算法也可以使用递归来实现。

一：单链表和单分支递归（只调用自身一次）

     讲个简单的例子：使用递归查找非空不带头节点的单链表的最后一个节点

并输出其数据域的值。

     先上代码：

void find(List L)
{
    if(L->next==NULL)
        printf(L->data);
    else
        find(L->next);
}

        再上这段代码的递归过程：

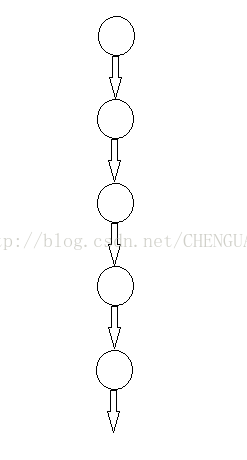
    从上面的例子我们可以看到，若递归函数每层只调用一次自身，

那么它的每一层的递归分支只有一条。而用这样的单分支实现的

递归一般都可以用简单的循环实现。代码如下：

void find(List L)
{
    while(L->next!=NULL)
    {
        L=L->next;
    }
    printf(L->data);
}

二：二叉树和双分支递归（调用自身两次）

    从二叉树的前序遍历开始，代码先行：

void traverse(TREE T)
{
    if(T==NULL)
        return;
    printf(T->data);
    traverse(T->lchild);
    traverse(T->rchild);
}

再上这段代码的递归过程：

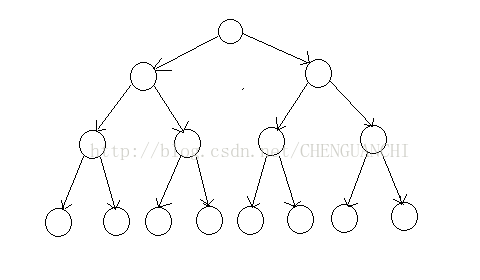
    从上面的例子我们可以看到，若递归函数每层调用两次自身，

那么它的每一层的递归分支就有两条。而用这样的双分支实现的

递归一般都较难用循环实现（需要用代码模拟栈的变化）。

    我们再看一个用到双分支递归的例子：

    一只青蛙可以跳上1级台阶，也可以跳上2级台阶，

请问这只青蛙跳上n级的台阶总共有多少种跳法？

    这个问题也可以简化为：青蛙每跳一次都有两种选择，一种是

跳一级，一种是跳两级。通过这样的描述，我们可以发现，这个

问题跟树的遍历问题很相似：二叉树的遍历每次都有两种选择，

一种往左，一种往右；青蛙每次跳台阶都有两种选择，一种跳

一级，一种跳两级。所以青蛙跳台阶问题可以借用二叉树遍历

算法的思想，采用双分支递归解决。

    递归过程依旧采用上图，

    递归代码是：

void jump(int sum)
{
    if(sum>n)//sum是已跳台阶级数和
        return;
    if(sum==n)
    {  
        cnt++;//cnt是符合要求的跳法个数
        return;
    }
    jump(sum+1);
    jump(sum+2);
}

    我们比较一下二叉树遍历代码和青蛙跳台阶算法，是不是有高度的相似性呢？