关于图
1.图是什么
图是一种基本逻辑结构(集合、线性结构、树形结构、图结构),在图的结构中,任意两个结点之间都可相关。
2.图的定义和术语
- 连通分量:是无向图中的极大连通子图。
- 强连通分量:是有向图中的极大连通子图。
- 生成树:一个连通图的生成树,是含有该连通图的全部顶点的一个极小连通子图。
图的存储结构
图有多种存储结构,包括邻接矩阵、邻接表、十字链表和邻接多重表等。
1.邻接矩阵
就是用矩阵来描述图中顶点之间的关联关系,在程序设计语言中用二维数组来实现矩阵。设G=(V,E)是一个图,其中V={v0, v1,...,vn-1},那么G的邻接矩阵A可定义如下的n阶方阵:
图的遍历方法
1.深度优先
假定以图中某个顶点vi为出发点,首先访问出发点vi,然后任选一个vi的未访问过的邻接点vj,以vj为新的出发点继续进行深度优先搜索,依次类推,直至图中所有顶点都被访问过。类似于树的先序遍历,图的深度优先搜索访问具有后进先出的特征,因此可以采用栈来实现,而且深度优先搜索的顶点的访问序列不是唯一的。
2.广度优先
从图中某个顶点vi出发,在访问了vi之后依次访问vi的所有邻接点,然后依次从这些邻接点出发按广度优先的搜索方法遍历图的其他顶点,直至所有顶点都被访问到。搜索邻接点的寻找具有先进先出的特征,可以使用队列来实现。这种访问的序列也不是唯一的。
图的应用
1.最小生成树
图的最小生成树就是权总和最小的生成树。构造最小生成树有两种基本方法,prim和kruskal。两者都是贪心的思想,Prim算法从顶点我角度出发,每次选择距离当前节点最近的节点加入,Kruskal算法从边的角度出发,每次只是选择权重最小的边加入。
(1)Prim算法
这种算法之所以可行,是基于这样一个判断:对于任意一个顶点vi,连接到该顶点的所有边中的一条最短边(vi, vj)必然属于最小生成树,也可以扩展为任意一个属于最小生成树的连通子图,从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树。
反证法:
假设权值最小的边不在最小生树中。
此时将权值最小的边加入生成树中,那么必然会构成一个回路,去掉回路中权值最大的边,构造一个新的树,这时与假设构成矛盾。所以权值最小的边一定在最小生成树中。
假设G=(V,E)是一个带权图,生成的最小生成树为MinT=(V,T),其中V为顶点集合,T为边的集合。求边的集合T的步骤如下:
- 初始化:U={u0},T={}。其中U为新设置的顶点集合,初始U中只含有顶点u0,即在构造最小生成树时从顶点u0出发。
- 对所有u ∈U,v ∈V-U的边(u,v)中,找一条权值最小的边(u‘,v’),将这条边加入到集合T中,将顶点v‘加入集合中。
- 如果U=V,则算法结束,否则重复以上两个步骤。
MST-PRIM(G, w, r)
for each u∈V
do key[u] ← ∞
parent[u]← NIL
key[r] ← 0
Q ← V
while Q ≠∅
do u ← EXTRACT-MIN(Q)
for each v∈Adj[u]
do if v∈Q and w(u, v) < key[v]
then parent[v] ← u
key[v] ← w(u, v)
G是无向连通图,r是起点。在算法的执行过程中,不在树中的所有顶点都放在一个基于key域的最小优先级队列Q中。key[v]表示所有将v与树中某一顶点相连的边中的最小权值,如果不存在这样的边,则key[v]=∞.
不管用什么方法,总共用时为O(V*T(Extraction)+E*T(DESCREASE)).
(1)如果用二叉堆来实现,总时间复杂度为O((E+V)logV)
(2)如果使用斐波那契堆,总时间复杂度为O(E+VlogV),因为Fib推update一次是O(1)。
(3)如果用数组来实现,总时间复杂度为O(V^2),因为从T(Extraction)是O(1),而T(Descrease)=O(1)
其实可以不使用优先队列,首先将根结点放入队列,第一次循环,取出队列顶点结点,将其退出队列,之后找到队列的结点的所有相邻顶点,若有更新,则更新它们的key值后,再将它们压入队列。重复操作直至队列空为止。
(2)Kruskal算法
通过从小到大遍历边集,每次尝试为最小生成树加入当前最短的边,加入成功的条件是该边不会在当已构建的图中造成回路,当加入的边的数目达到n-1,遍历结束。
MST-KRUSKAL(G, W)
A←∅
for each vertex v∈V[G]
do MAKE-SET(v)
sort the eages of E into nondecreasing order by weight w
for each eage(u, v)∈E, teken in nondecreasing order by weight
do if(FIND-SET(u) ≠ FIND-SET(v))
then A←A∪{ (u, v) }
Union(u, v)
return A
Kruskal算法在图上的运行时间取决于不相交集合数据结构是如何实现的。
2.最短路径
(1)Dijkstra算法
单源最短路径的算法,前提不能有负权边和孤立点。
- 贪心算法:每次找最近的点,局部最优等于全局最优,数学归纳法可证。
- 维护起点start到每个点的距离。
- 时间复杂度O(n^2)
- 附加空间复杂度O(n)
Dijkstra 算法伪代码:
Q = {} // 已求出到 start 点最短路的点集合,初始为空
d[s] = 0, 其余值为正无穷大
while (|Q| < |V|) // 数学符号|A|表示集合A的点数
取出不在Q中的最小的d[i]
for (i相邻的点j,j不属于Q)
d[j] = min(d[j], d[i] + c[i][j]) //维护距离
Q = Q + {i}
(2)Floyd算法
求出图中任意两点最短路,对负权边仍然有效。
- 动态规划:每次加入一个点。
- 维护任意两点间的距离
- 时间复杂度O(n^3)
- 附加空间复杂度O(n^2)
Floyd 算法伪代码:
for k in range(0, n):
for i in range(0, n):
for j in range(0, n):
g[i][j] = min(g[i][j], g[i][k]+g[k][j])
3.拓扑排序
是一个有向无环图的所有顶点的线性序列。
(1)关键路径
在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,边上的权值表示活动的持续时间,称这样的有向图为边表示活动的网,简称AOE网。
在AOE网中,从始点到终点具有最大路径长度(该路径上的各个路径所持续的时间之和)的路径为关键路径。
- 事件的最早发生时间ve[k]
ve[k]是指从始点开始到顶点vk的最大路径长度,这个长度决定了所有从顶点vk发出的活动能够开工的最早时间。
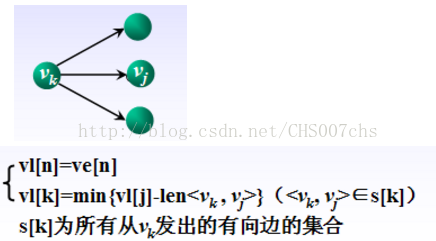
- 事件的最迟发生时间vl[k]
是指在不推迟整个工期的前提下,事件vk允许的最晚发生时间。
- 活动的最早开始时间
若活动ai由弧<vk, vj>表示,则活动ai的最早开始时间应该等于事件vk的最早发生时间,因此e[i]=ve[k]。
- 活动的最晚开始时间
活动ai的最晚开始时间,若ai由弧<vk,vj>表示,则ai的最晚开始时间要保证事件vj的最迟时间不拖后,因此:l[i] = vl[j]-len<vk,vj>
那么关键路径即为e[i]=l[i]的路径。
最后欢迎大家访问我的个人网站:1024s
























 118
118

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








