菜菜学dp系列之1 2013.07.30-CSDN博客

本文链接：https://blog.csdn.net/HuaiZuoWoZuo/article/details/9628857

菜菜最近通过自学看了关于动态规划方面的书不多也不算很少（不敢跟大神比~），看来看去也没彻底明白“动态规划”她到底是个啥- -现在菜菜准备静下心来拿出我那几本传家红宝书来和大家一起分享此次学习的经历哈^^

动态规划通常来求解最优化问题。这类问题可以有很多可行解，每个解都有一个值，我们希望找到最优值（最大值或最小值）的解。我们称这样的解为问题的一个最优解，而不是最优解，因为可能有多个解都达到最优值（ps:按菜菜的yy就是说最优解不唯一，且我们后面学习的最长公共子序列也是不唯一的）。

算导上说设计一个动态规划算法通常需要4步：

step1：刻画一个最优解的结构特征.

step2：递归地定义最优解的值.

step3：计算最优解的值，通常采用自底向上的方法.

step4：利用计算出的信息构造一个最优解.

（所谓的自底向上方法就是使任何子问题的求解都只会依赖于“更小的”子问题求解。）

这里有一个补充点:

*.动态规划的核心是状态和状态转移方程.

ex 1&最长公共子序列问题（LSC）

菜菜觉得基本概念的不说了，一目了然。先介绍这个LCS最有子结构的定理吧：

Prefix:给定一个序列X=<x1,x2,...,xm>,对i=0,1,2,3,...，m,定义X的第i Prefix为Xi=<x1,x2,x3,...,xi>。例如，若X=<x1,x2,...,xi>。例如，若X=<A,B,C,B,D,A,B>,则X4=<A,B,C,B>，X0为空串。

定理ex1(LCS的最优子结构)令X=<x1,x2,x3,...,xm>和Y=<y1,y2,y3,...,yn>为两个序列，Z=<z1,z2,...,zk>为X和Y的任意LCS。

1.如果xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的一个LCS.

2.如果xm!=yn（注意这里"!="是不等于号，为了方便才这样写的，大家懂的哈~~），那么zk！=xm意味着Z是Xm-1和Y的一个 LCS .

3.如果xm！=yn，那么zk！=yn意味着Z是X和Yn-1的一个LCS.

（证明略，搜书上谷歌）

设有二维数组 $f[i][j]$ 表示 $X$ 的 $i$ 位和 $Y$ 的 $j$ 位之前的最长公共子序列的长度，则有：

$f[1][1] = same(1,1)$

$f[i][j] = max\{f[i-1][j-1] + same(i,j), f[i-1][j],f[i][j-1]\}$

其中， $same(a,b)$ 当 $X$ 的第 $a$ 位与 $Y$ 的第 $b$ 位完全相同时为“1”，否则为“0”。

此时， $f[i][j]$ 中最大的数便是 $X$ 和 $Y$ 的最长公共子序列的长度，依据该数组回溯，便可找出最长公共子序列。

该算法的空间、时间复杂度均为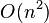 $O(n^{2})$ ，经过优化后，空间复杂度可为 $O(n)$ ，时间复杂度为 $O(n\log n)$ 。

附录:下文为动态规划的基本算法

 
      #include "stdafx.h" 
     
      #include <iostream> 
     
      using 
       namespace 
       std; 
     
      const 
       int 
       size = 13;  
      // 11个活动，加上虚构活动a0和an+1 
     
      // 动态规划：构造最优解 
     
      void 
       recursive_activity_selector( 
      int 
       s[],  
      int 
       f[],  
      int 
       c[],  
      int 
       p[][size],  
      int 
       num) 
     
      { 
     
      for 
       ( 
      int 
       i = 0; i < num; ++i) 
     
      for 
       ( 
      int 
       j = 1; j < num; ++j) 
     
      if 
       (i >= j) 
     
      c[i][j] = 0; 
     
      else 
     
      for 
       ( 
      int 
       k = i + 1; k < j; k++) 
     
      if 
       (f[i] <= s[k] && f[k] <= s[j])  
      // 习题答案和很多网友给出的伪代码或实现都没有这句，显然有问题 
     
      if 
       (c[i][j] < c[i][k] + c[k][j] + 1) { 
     
      c[i][j] = c[i][k] + c[k][j] + 1; 
     
      p[i][j] = k; 
     
      } 
     
      } 
     
      // 动态规划：输出最优解 
     
      void 
       print( 
      int 
       i,  
      int 
       j,  
      int 
       p[][size]) 
     
      { 
     
      int 
       k = 0; 
     
      if 
       (p[i][j] == 0) 
     
      return 
       ; 
     
      cout << p[i][j] <<  
      " " 
      ; 
     
      print(i, p[i][j], p); 
     
      print(p[i][j], j, p); 
     
      } 
     
      // 贪心算法：递归版本 
     
      void 
       recursive_activity_selector( 
      int 
       s[],  
      int 
       f[],  
      int 
       i,  
      int 
       n,  
      int 
       c[][size]) 
     
      { 
     
      int 
       m = i + 1; 
     
      while 
       (m <= n && s[m] < f[i]) 
     
      ++m; 
     
      if 
       (m < n) { 
     
      c[i][n] = m; 
     
      recursive_activity_selector(s, f, m, n, c); 
     
      } 
     
      } 
     
      // 贪心算法：迭代版本 
     
      void 
       greedy_activity_selector( 
      int 
       s[],  
      int 
       f[],  
      int 
       i,  
      int 
       n,  
      int 
       c[][size]) 
     
      { 
     
      for 
       ( 
      int 
       m = 1; m < n; ++m) 
     
      if 
       (s[m] >= f[i]) { 
     
      c[i][n] = m; 
     
      i = m; 
     
      } 
     
      } 
     
      int 
       main() 
     
      { 
     
      int 
       s[size] = {65535,1,3,0,5,3,5,6,8,8,2,12,65535};  
      // 开始时间 
     
      int 
       f[size] = {0,4,5,6,7,8,9,10,11,12,13,14,0};  
      // 结束时间 
     
      int 
       c[size][size] = {0}; 
     
      int 
       p[size][size] = {0}; 
     
      recursive_activity_selector(s, f, c, p, size); 
     
      for 
       ( 
      int 
       i = 0; i < size; i++) { 
     
      for 
       ( 
      int 
       j = 0; j < size; j++) 
     
      cout << p[i][j] <<  
      " " 
      ; 
     
      cout << endl; 
     
      } 
     
      cout << endl; 
     
      print(0, size - 1, p); 
     
      system 
      ( 
      "pause" 
      ); 
     
      return 
       0; 
     
      }