基础算法排序之分治排序

写在之前的话:
    对于博文的内容出现的本人观点(博文中的内容有的摘自于算法导论)的不当或者错误而对你造成困扰的话，你可以尽情的鄙视与吐槽，最好写出你的观点，本人定当虚心受教。
分而治之，顾名思义也就是将原问题的规模分解成一系列规模小的子问题,算法导论中是这么说的:
分治模式在每一层递归上都有三个步骤:
    分解: 将原问题分解成一系列子问题;
    解决: 递归地解决各子问题。若子问题足够小，则直接求解
    合并： 将子问题的结果合并成原问题的解
1.合并排序
    合并排序完全依照了上述模式,直观的操作如下:  
    分解：将n个元素分成含n/2个元素的子序列
    解决：用合并排序法对两个子序列递归的排序
    合并：合并两个已排序的子序列以得到排序结果
    

    合并排序的关键步骤在于对于两个已经排好的数组进行合并，当然如同前面的增量式排序,这边的两个已经排好的数组指的也是通过数组的序号进行分割的子序列，下面就称子序列，而合并的算法也很简单，将两个已经排好的子序列分别用两个临时数组A,B保存，然后将A数组中的元素与B数组中的元素逐个比较，比较小的就放进原数组中，这样就将两个子序列就可以合并成一个排好序的序列.

void merge(int a[], int start1, int end1, int end2) {
  int length = end2 - start1 + 1, start2 = end1 + 1;  
  int l_length = end1 - start1 + 1, r_length = end2 - start2 + 1, i = 0, j = 0, k = 0;;
  //临时保存左右两部分需要合并的数组
  int *l_array = (int *) malloc (sizeof(int) * l_length);
  int *r_array = (int *) malloc (sizeof(int) * r_length);

  for ( ; i < l_length; i++) {
    l_array[i] = a[start1 + i];
  }
  i = 0;
  for (; i < r_length; i++) {
    r_array[i] = a[start2 + i];
  }

  i = 0;
  while (i < length && k < r_length && j < l_length) {
    if (l_array[j] > r_array[k]) {
      a[start1+i] = r_array[k];
      k ++;
    } else {
      a[start1+i] = l_array[j];
      j ++;
    }
    i ++;
  }
  for (; j < l_length; j++) {
    a[start1+i] = l_array[j];
    i ++;
  }
  for (; k < r_length; k++) {
    a[start1+i] = r_array[k];
    i ++;
  }
  free(l_array);
  free(r_array);
}

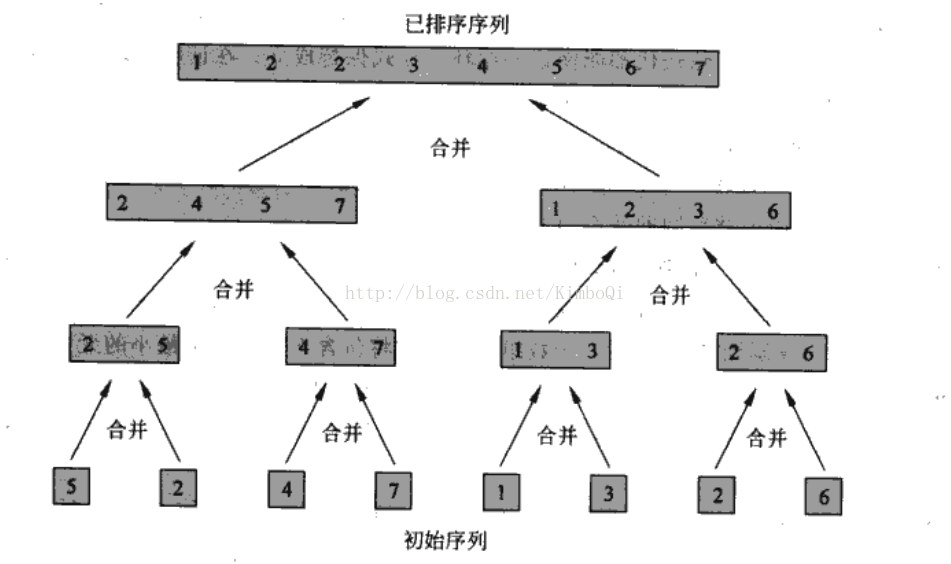
    合并的问题解决了，现在说分解和解决,如果了解树的后序遍历的话分解的话就很容易想通了，二叉树的每一棵子树对应于合并排序二分后分成的两个序列，整个的分解与合并其实就是一棵二叉树后序遍历的过程，不同的是二叉树的遍历只是访问节点，而合并排序需要的是将左子树和右子树合并成一个新的序列并作为左右子树的父节点。这样到最后根节点的时候左右序列就合并成一个排序好的数组了。

void merge_sort(int a[], int p, int r) {
  if (p < r) {
    int q = (p + r) / 2;
    merge_sort(a, p, q);
    merge_sort(a, q + 1, r);
    printf ("p: %d   r: %d\n", p, r);
    merge(a, p, q, r);
  }
}

    

2.快速排序

    快速排序也是一种分治策略下的排序算法。按照模式直观的操作如下：
    分解：数组A[p..r]被划分成两个子序列A[p..q-1]和A[q+1..r],使得A[p..q-1]中的每个元素都小于等于A[q]，而且，小于等于A[q+1..r]中的元素。下标q也在这个划分过程中进行计算。
    解决：通过递归调用快速排序，对子数组A[p..q-1]和A[q+1..r]
    合并：因为两个子数组是就地排序的，将它们的合并不许要操作：整个数组A[p..r]已排序
    
    快排的关键步骤在于分解，在分解的过程中将一个数组分成两个部分，如果按照非递减排序，每一次递归过程的子序列中,前半部分都是小于等于后半部分,而分割的分割位置就在前半部分与后半部分的中间位置。要对数组做这样的一个过程，还是比较容易的，但在快速排序中采用的是就地排序,不借助于任何临时存储，数组元素的移动只在原数组中完成。分解的算法如下：

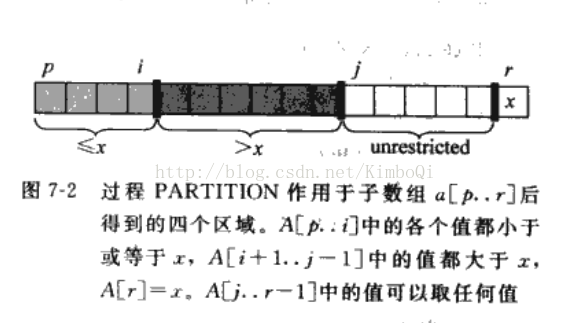
    每一次迭代，将一个序列当作是四个子序列组成，分别是上述的第一部分，第二部分，以及未成为以上两部分的第三部分还有就是中间元素，挺绕人的看图吧

    在算法执行之前，先取序列的最后一个元素为中间值x，第三部分图中定义为unrestricted，表示还未确定属于第一部分还是第二部分的所有元素，算法结束后第三部分所有的元素都会被加入到第一部分或者第二部分中。数组的范围是a[p..r],r表示中间元素x的索引。假设定义第三部分的初始范围用变量表示是[j..r-1](j=p).用变量i来确定第一部分与第二部分的分割，a[i]是属于第一部分的。当初始时第一部分的数组是为空的，那就使得i=p-1,因为如果i=p的话第一个元素就变成了第一部分了。所有的部分范围用变量表示为：
第一部分 [p..i]
第二部分 [i+1..j-1]
第三部分 [j..r-1]
第四部分 [r]
    
    算法过程也就相对简单了，取第三部分的第一个元素与中间元素也就是a[r]比较，会有两种情况:
    1. 如果小于或者等于a[r]就将i+1，这样就等于将第一部分增加了一个元素
    2. 如果大于a[r]就将j+1,其实也就是将第二部分增加了一个元素
    等第三部分没有了，也就是 j==r-1了，将a[i+1]与a[r]交换，算法结束。

    解决的话就很类似于二叉树的先序遍历了，不同于访问根节点，快排的每次访问是将左右子树分成两个部分，如果是按非递减排序，左子树的所有元素小于等于右子树，并且根节点是中间元素，到完成遍历后一棵二叉查找树（当然二叉查找树是不包含相等元素的节点的）也就产生了，这部分就靠自己想象吧！

int partition(int a[], int start, int end){
  int x = a[end], i = start-1, temp;
  int j = start;
  for (; j < end; j++) {
    if (a[j] <= x) {
      i ++;
      temp = a[j];
      a[j] = a[i];
      a[i] = temp;
    }
  }
  temp = a[i+1];
  a[i+1] = a[end];
  a[end] = temp;
  return i+1;
}

void quick_sort(int a[], int p, int r) {
  if (p < r) {
    int q = partition(a, p, r);
    quick_sort(a, p, q-1);
    quick_sort(a, q+1, r);
  }
}