对多元二次函数的理解
本学期学习了《工程优化》的课程,平时没有好好地上课听讲,快考试了才发现这门课程还是挺有用的。老师上课讲的优化问题都是针对多元二次函数的,而且大部分是二元二次,比较简单。之前自己并没有对多元二次函数有过多认识,学东西也是浑沦吞枣,这两天细细地看书,感觉多元二次函数的图像特别有意思。
这里,我们以二元二次函数为例,利用MATLAB对其进行可视化。
一、先以一个二次型为例:
函数形式为
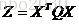
例如函数:
Z=X1.^2+X2.^2,
X1,X2取值范围为[-6,6],
其图形为:
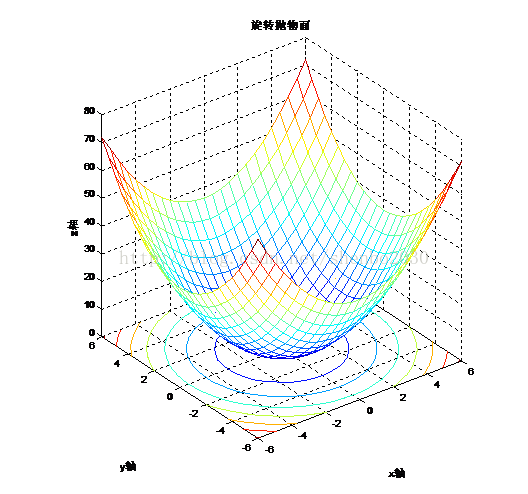
因为上述二次型的Q为正定对称矩阵,所以这明显是一个凸函数,且最优值唯一。
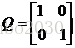
观察上图可知,它的等高线都是以(0,0)为圆心的圆族,圆心处就是最优解。
对上式进行稍加改变:
Z=X1.^2+X2.^2+1*X1.*X2,X1,X2取值范围为[-6,6],图形变化为:
此时,函数同样是一个凸函数,因为Q同样是正定矩阵,此时,
但是它的等高线已不是圆,而是一个椭圆族。
而此时如果把函数改为:
Z=X1.^2+X2.^2+2*X1.*X2,X1,X2取值范围为[-6,6],图形变化为:
此时,函数已经不再是凸函数,因为Q已经不再是正定矩阵。此时,
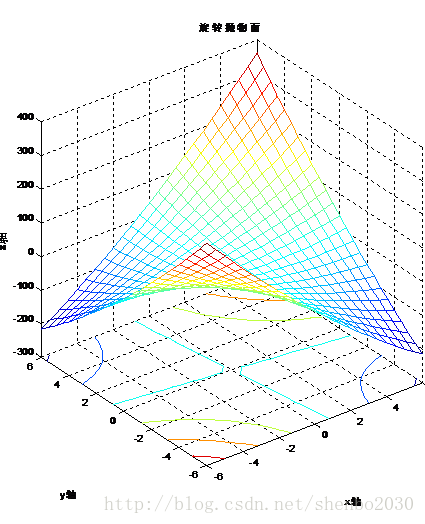
函数为Z=X1.^2+X2.^2+8*X1.*X2时,图形为:
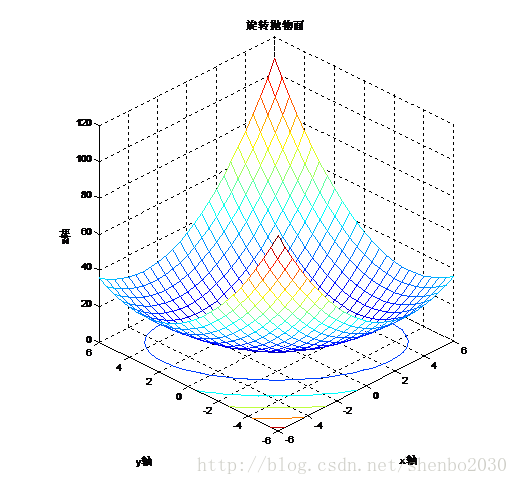
下面,看一下标准形式的二次函数图像,其函数形式为:
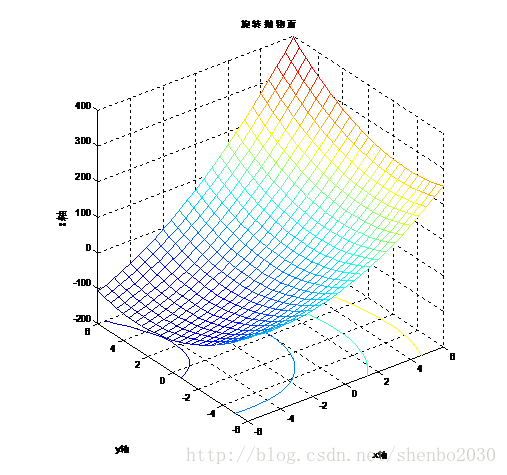
从图像看,好像此时的函数已经不是凸函数,等高线也不是闭合曲线,其实这样下结论是错的。此时的Q为
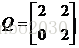
不难判断Q正定,所以函数应该是严格凸函数。实际上,完整的图像应该如下所示,上图是受限于X的取值范围所致。

此时的取值范围为[-60,60]。所以二次函数的凹凸性与b,c无关,至于矩阵Q有关。
上面的工作只是简单地对二次函数进行了可视化,没有什么技术可言,还望看客不要取笑。下面提供画一些高数中的函数图像的程序和这些函数的图像。
一、螺旋线
1.静态螺旋
a=0:0.1:20*pi;
h=plot3(a.*cos(a),a.*sin(a),2.*a,'b','linewidth',2);
axis([-50,50,-50,50,0,150]);
grid on
set(h,'erasemode','none','markersize',22);
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('静态螺旋线');
<








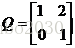

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章














 3329
3329











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








