一、文章来由
上一篇提到了网络加密算法中,非对称加密算法是现代网络安全的基石,而RSA算法是公钥加密算法中应用最广的算法之一。
二、RSA算法的基础
1、互斥关系
大家都知道,一个很大很大的数很难进行因式分解。
如果两个正整数,除了1以外,没有其他公因子,我们就称这两个数是互质关系(coprime)。比如,15和32没有公因子,所以它们是互质关系。这说明,不是质数也可以构成互质关系。
同时有以下结论:
(1) 任意两个质数构成互质关系,比如13和61。
(2) 一个数是质数,另一个数只要不是前者的倍数,两者就构成互质关系,比如3和10。
(3)如果两个数之中,较大的那个数是质数,则两者构成互质关系,比如97和57。
(4)1和任意一个自然数是都是互质关系,比如1和99。
(5)p是大于1的整数,则p和p-1构成互质关系,比如57和56。
(6)p是大于1的奇数,则p和p-2构成互质关系,比如17和15。
2、欧拉函数&&欧拉定理
欧拉函数定义如下:
任意给定正整数n,请问在小于等于n的正整数之中,有多少个与n构成互质关系?(比如,在1到8之中,有多少个数与8构成互质关系?)
计算这个值的方法就叫做欧拉函数,以φ(n)表示。在1到8之中,与8形成互质关系的是1、3、5、7,所以 φ(n) = 4。
关于欧拉函数的几种情况详见阮一峰的博客:
http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html
欧拉定理定义如下:
欧拉函数的用处,在于欧拉定理。”欧拉定理”指的是:
如果两个正整数a和n互质,则n的欧拉函数 φ(n) 可以让下面的等式成立:
也就是说,a的φ(n)次方被n除的余数为1。或者说,a的φ(n)次方减去1,可以被n整除。比如,3和7互质,而7的欧拉函数φ(7)等于6,所以3的6次方(729)减去1,可以被7整除(728/7=104)。
欧拉定理可以大大简化某些运算。比如,7和10互质,根据欧拉定理,已知 φ(10) 等于4,所以马上得到7的4倍数次方的个位数肯定是1。
因此,7的任意次方的个位数(例如7的222次方),心算就可以算出来(只需与4比较,进而心算)。
3、模反元素
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1。b就叫做a的”模反元素”。
比如,3和11互质,那么3的模反元素就是4,因为 (3 × 4)-1 可以被11整除。显然,模反元素不止一个, 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…},即如果b是a的模反元素,则 b+kn 都是a的模反元素。
三、正式进入RSA算法
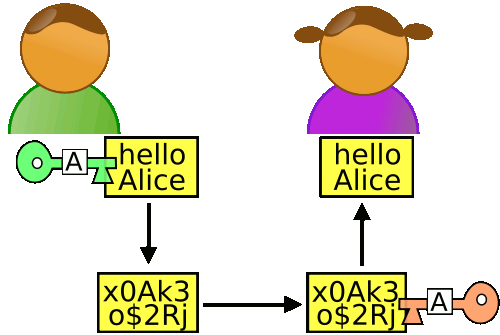
假设爱丽丝要与鲍勃进行加密通信,她该怎么生成公钥和私钥呢?
第一步,随机选择两个不相等的质数p和q
爱丽丝选择了61和53。(实际应用中,这两个质数越大,就越难破解。)
第二步,计算p和q的乘积n
爱丽丝就把61和53相乘。
n = 61×53 = 3233
n的长度就是密钥长度。3233写成二进制是110010100001,一共有12位,所以这个密钥就是12位。实际应用中,RSA密钥一般是1024位,重要场合则为2048位。
第三步,计算n的欧拉函数φ(n)
根据公式:
φ(n) = (p-1)(q-1)
爱丽丝算出φ(3233)等于60×52,即3120。
第四步,随机选择一个整数e
条件是1< e < φ(n),且e与φ(n) 互质。
爱丽丝就在1到3120之间,随机选择了17。(实际应用中,常常选择65537)
第五步,计算e对于φ(n)的模反元素d
所谓”模反元素”就是指有一个整数d,可以使得ed被φ(n)除的余数为1。
ed ≡ 1 (mod φ(n))
这个式子等价于
ed - 1 = kφ(n)
于是,找到模反元素d,实质上就是对下面这个二元一次方程求解。
ex + φ(n)y = 1
已知 e=17, φ(n)=3120,
17x + 3120y = 1
方程求解过程省略。
爱丽丝算出一组整数解为 (x,y)=(2753,-15),即 d=2753。
至此所有计算完成。
第六步,将n和e封装成公钥,n和d封装成私钥
n—p*q = 61×53 = 3233
e—随机选择一个整数e,条件是1< e < φ(n),且e与φ(n) 互质。
d—e对于φ(n)的模反元素d
在爱丽丝的例子中,n=3233,e=17,d=2753,所以公钥就是 (3233,17),私钥就是(3233, 2753)。
实际应用中,公钥和私钥的数据都采用ASN.1格式表达(实例)。
四、为什么RSA算法可靠
那么为什么RSA就可靠呢?
有无可能在已知n和e的情况下,推导出d?
(1)ed≡1 (mod φ(n))。只有知道e和φ(n),才能算出d。
(2)φ(n)=(p-1)(q-1)。只有知道p和q,才能算出φ(n)。
(3)n=pq。只有将n因数分解,才能算出p和q。
结论:如果n可以被因数分解,d就可以算出,也就意味着私钥被破解。
可是,大整数的因数分解,是一件非常困难的事情。目前,除了暴力破解,还没有发现别的有效方法。
而且d(模反元素)还不是唯一的
五、加解密过程
用事例说话。
(1)加密要用公钥 (n,e)
假设鲍勃要向爱丽丝发送加密信息m,他就要用爱丽丝的公钥 (n,e) 对m进行加密。这里需要注意,m必须是整数(字符串可以取ascii值或unicode值),且m必须小于n。
所谓”加密”,就是算出下式的c:
m^e ≡ c (mod n)
爱丽丝的公钥是 (3233, 17),鲍勃的m假设是65,那么可以算出下面的等式:
65^17 ≡ 2790 (mod 3233)
于是,c等于2790,鲍勃就把2790发给了爱丽丝。
(2)解密要用私钥(n,d)
爱丽丝拿到鲍勃发来的2790以后,就用自己的私钥(3233, 2753) 进行解密。可以证明,下面的等式一定成立:
c^d ≡ m (mod n)
也就是说,c的d次方除以n的余数为m。现在,c等于2790,私钥是(3233, 2753),那么,爱丽丝算出
27902753 ≡ 65 (mod 3233)
因此,爱丽丝知道了鲍勃加密前的原文就是65。
我们可以看到,如果不知道d,就没有办法从c求出m。而前面已经说过,要知道d就必须分解n,这是极难做到的,所以RSA算法保证了通信安全。
你可能会问,公钥(n,e) 只能加密小于n的整数m,那么如果要加密大于n的整数,该怎么办?
有两种解决方法:一种是把长信息分割成若干段短消息,每段分别加密;另一种是先选择一种”对称性加密算法”(比如DES),用这种算法的密钥加密信息,再用RSA公钥加密DES密钥(注意只是密钥)。
具体的加解密证明详见:http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html
参考文献
[1] http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html










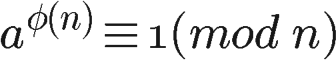
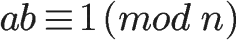














 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








