--摘自维基百科
红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由鲁道夫·贝尔发明的,他称之为"对称二叉B树",它现代的名字是在 Leo J. Guibas 和 Robert Sedgewick 于1978年写的一篇论文中获得的。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n是树中元素的数目。
用途和好处
红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。这不只是使它们在时间敏感的应用如实时应用(real time application)中有价值,而且使它们有在提供最坏情况担保的其他数据结构中作为建造板块的价值;例如,在计算几何中使用的很多数据结构都可以基于红黑树。
红黑树在函数式编程中也特别有用,在这里它们是最常用的持久数据结构之一,它们用来构造关联数组和集合,在突变之后它们能保持为以前的版本。除了O(log n)的时间之外,红黑树的持久版本对每次插入或删除需要O(log n)的空间。
红黑树是 2-3-4树的一种等同。换句话说,对于每个 2-3-4 树,都存在至少一个数据元素是同样次序的红黑树。在 2-3-4 树上的插入和删除操作也等同于在红黑树中颜色翻转和旋转。这使得 2-3-4 树成为理解红黑树背后的逻辑的重要工具,这也是很多介绍算法的教科书在红黑树之前介绍 2-3-4 树的原因,尽管 2-3-4 树在实践中不经常使用。
性质
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根是黑色。
性质3. 所有叶子都是黑色(叶子是NIL节点)。
性质4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
要知道为什么这些特性确保了这个结果,注意到属性4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据属性5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
在很多树数据结构的表示中,一个节点有可能只有一个子节点,而叶子节点包含数据。用这种范例表示红黑树是可能的,但是这会改变一些属性并使算法复杂。为此,本文中我们使用 "nil 叶子" 或"空(null)叶子",如上图所示,它不包含数据而只充当树在此结束的指示。这些节点在绘图中经常被省略,导致了这些树好像同上述原则相矛盾,而实际上不是这样。与此有关的结论是所有节点都有两个子节点,尽管其中的一个或两个可能是空叶子。
操作
因为每一个红黑树也是一个特化的二叉查找树,因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而,在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的属性需要少量(O(log n))的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。虽然插入和删除很复杂,但操作时间仍可以保持为 O(log n) 次。
插入
我们首先以二叉查找树的方法增加节点并标记它为红色。(如果设为黑色,就会导致根到叶子的路径上有一条路上,多一个额外的黑节点,这个是很难调整的。但是设为红色节点后,可能会导致出现两个连续红色节点的冲突,那么可以通过颜色调换(color flips)和树旋转来调整。) 下面要进行什么操作取决于其他临近节点的颜色。同人类的家族树中一样,我们将使用术语叔父节点来指一个节点的父节点的兄弟节点。注意:
在下面的示意图中,将要插入的节点标为N,N的父节点标为P,N的祖父节点标为G,N的叔父节点标为U。在图中展示的任何颜色要么是由它所处情形所作的假定,要么是这些假定所暗含 (imply) 的。
对于每一种情况,我们将使用 C 示例代码来展示。通过下列函数,可以找到一个节点的叔父和祖父节点:
node grandparent<span class="br0">(</span>node n<span class="br0">)</span> <span class="br0">{</span>
<span class="kw1">return</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
node uncle<span class="br0">(</span>node n<span class="br0">)</span> <span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent <span class="sy0" style="color: rgb(51, 153, 51);">==</span> grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="br0">)</span>
<span class="kw1">return</span> grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">else</span>
<span class="kw1">return</span> grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
情形1: 新节点N位于树的根上,没有父节点。在这种情形下,我们把它重绘为黑色以满足性质2[5]。因为它在每个路径上对黑节点数目增加一,性质5[4]符合。
<span class="kw4" style="color: rgb(153, 51, 51);">void</span> insert_case1<span class="br0">(</span>node n<span class="br0">)</span> <span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent <span class="sy0" style="color: rgb(51, 153, 51);">==</span> NULL<span class="br0">)</span>
n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">else</span>
insert_case2<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
情形2: 新节点的父节点P是黑色,所以性质4[3]没有失效(新节点是红色的)。在这种情形下,树仍是有效的。性质5[4]也未受到威胁,尽管新节点N有两个黑色叶子子节点;但由于新节点N是红色,通过它的每个子节点的路径就都有同通过它所取代的黑色的叶子的路径同样数目的黑色节点,所以依然满足这个性质。
<span class="kw4" style="color: rgb(153, 51, 51);">void</span> insert_case2<span class="br0">(</span>node n<span class="br0">)</span> <span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span>
<span class="kw1">return</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span> <span class="coMULTI" style="color: rgb(128, 128, 128); font-style: italic;">/* 树仍旧有效 */</span>
<span class="kw1">else</span>
insert_case3<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
注意: 在下列情形下我们假定新节点的父节点为红色,所以它有祖父节点;因为如果父节点是根节点,那父节点就应当是黑色。所以新节点总有一个叔父节点,尽管在情形4和5下它可能是叶子节点。
|
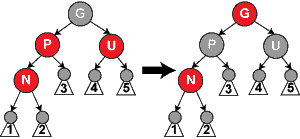
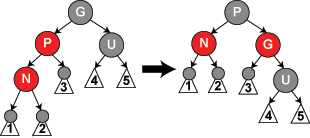
情形3: 如果父节点P和叔父节点U二者都是红色,(此时新插入节点N做为P的左子节点或右子节点都属于情形3,这里右图仅显示N做为P左子的情形)则我们可以将它们两个重绘为黑色并重绘祖父节点G为红色(用来保持性质5[4])。现在我们的新节点N有了一个黑色的父节点P。因为通过父节点P或叔父节点U的任何路径都必定通过祖父节点G,在这些路径上的黑节点数目没有改变。但是,红色的祖父节点G的父节点也有可能是红色的,这就违反了性质4[3]。为了解决这个问题,我们在祖父节点G上递归地进行情形1的整个过程。(把G当成是新加入的节点进行各种情况的检查) |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span> insert_case3<span class="br0">(</span>node n<span class="br0">)</span> <span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>uncle<span class="br0">(</span>n<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">!=</span> NULL <span class="sy0" style="color: rgb(51, 153, 51);">&&</span> uncle<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> RED<span class="br0">)</span> <span class="br0">{</span>
n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
uncle<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> RED<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
insert_case1<span class="br0">(</span>grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
<span class="kw1">else</span>
insert_case4<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
注意: 在余下的情形下,我们假定父节点P 是其父亲G 的左子节点。如果它是右子节点,情形4和情形5中的左和右应当对调。
|
情形4: 父节点P是红色而叔父节点U是黑色或缺少,并且新节点N是其父节点P的右子节点而父节点P又是其父节点的左子节点。在这种情形下,我们进行一次左旋转调换新节点和其父节点的角色; 接着,我们按情形5处理以前的父节点P以解决仍然失效的性质4[3]。注意这个改变会导致某些路径通过它们以前不通过的新节点N(比如图中1号叶子节点)或不通过节点P(比如图中3号叶子节点),但由于这两个节点都是红色的,所以性质5[4]仍有效。 |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span> insert_case4<span class="br0">(</span>node n<span class="br0">)</span> <span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right <span class="sy0" style="color: rgb(51, 153, 51);">&&</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent <span class="sy0" style="color: rgb(51, 153, 51);">==</span> grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="br0">)</span> <span class="br0">{</span>
rotate_left<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
n <span class="sy0" style="color: rgb(51, 153, 51);">=</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span> <span class="kw1">else</span> <span class="kw1">if</span> <span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left <span class="sy0" style="color: rgb(51, 153, 51);">&&</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent <span class="sy0" style="color: rgb(51, 153, 51);">==</span> grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="br0">)</span> <span class="br0">{</span>
rotate_right<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
n <span class="sy0" style="color: rgb(51, 153, 51);">=</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
insert_case5<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
|
情形5: 父节点P是红色而叔父节点U 是黑色或缺少,新节点N 是其父节点的左子节点,而父节点P又是其父节点G的左子节点。在这种情形下,我们进行针对祖父节点G 的一次右旋转; 在旋转产生的树中,以前的父节点P现在是新节点N和以前的祖父节点G 的父节点。我们知道以前的祖父节点G是黑色,否则父节点P就不可能是红色 (如果 P 和 G 都是红色就违反了性质4,所以 G 必须是黑色)。我们切换以前的父节点P和祖父节点G的颜色,结果的树满足性质4[3]。性质5[4]也仍然保持满足,因为通过这三个节点中任何一个的所有路径以前都通过祖父节点G ,现在它们都通过以前的父节点P。在各自的情形下,这都是三个节点中唯一的黑色节点。 |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span> insert_case5<span class="br0">(</span>node n<span class="br0">)</span> <span class="br0">{</span>
n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> RED<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left <span class="sy0" style="color: rgb(51, 153, 51);">&&</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent <span class="sy0" style="color: rgb(51, 153, 51);">==</span> grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="br0">)</span> <span class="br0">{</span>
rotate_right<span class="br0">(</span>grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span> <span class="kw1">else</span> <span class="br0">{</span>
<span class="coMULTI" style="color: rgb(128, 128, 128); font-style: italic;">/* Here, n == n->parent->right && n->parent == grandparent(n)->right */</span>
rotate_left<span class="br0">(</span>grandparent<span class="br0">(</span>n<span class="br0">)</span><span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
<span class="br0">}</span>
注意插入实际上是原地算法,因为上述所有调用都使用了尾部递归。
删除
如果需要删除的节点有两个儿子,那么问题可以被转化成删除另一个只有一个儿子的节点的问题(为了表述方便,这里所指的儿子,为非叶子节点的儿子)。对于二叉查找树,在删除带有两个非叶子儿子的节点的时候,我们找到要么在它的左子树中的最大元素、要么在它的右子树中的最小元素,并把它的值转移到要删除的节点中(如在这里所展示的那样)。我们接着删除我们从中复制出值的那个节点,它必定有少于两个非叶子的儿子。因为只是复制了一个值而不违反任何属性,这就把问题简化为如何删除最多有一个儿子的节点的问题。它不关心这个节点是最初要删除的节点还是我们从中复制出值的那个节点。
在本文余下的部分中,我们只需要讨论删除只有一个儿子的节点(如果它两个儿子都为空,即均为叶子,我们任意将其中一个看作它的儿子)。如果我们删除一个红色节点(此时该节点的儿子将都为叶子节点),它的父亲和儿子一定是黑色的。所以我们可以简单的用它的黑色儿子替换它,并不会破坏属性3和4。通过被删除节点的所有路径只是少了一个红色节点,这样可以继续保证属性5。另一种简单情况是在被删除节点是黑色而它的儿子是红色的时候。如果只是去除这个黑色节点,用它的红色儿子顶替上来的话,会破坏属性5,但是如果我们重绘它的儿子为黑色,则曾经通过它的所有路径将通过它的黑色儿子,这样可以继续保持属性5。
需要进一步讨论的是在要删除的节点和它的儿子二者都是黑色的时候,这是一种复杂的情况。我们首先把要删除的节点替换为它的儿子。出于方便,称呼这个儿子为N,称呼它的兄弟(它父亲的另一个儿子)为S。在下面的示意图中,我们还是使用P称呼N的父亲,SL称呼S的左儿子,SR称呼S的右儿子。我们将使用下述函数找到兄弟节点:
<span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>
sibling<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="br0">)</span>
<span class="kw1">return</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">else</span>
<span class="kw1">return</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
我们可以使用下列代码进行上述的概要步骤,这里的函数 replace_node 替换 child 到 n 在树中的位置。出于方便,在本章节中的代码将假定空叶子被用不是 NULL 的实际节点对象来表示(在插入章节中的代码可以同任何一种表示一起工作)。
<span class="kw4" style="color: rgb(153, 51, 51);">void</span>
delete_one_child<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="coMULTI" style="color: rgb(128, 128, 128); font-style: italic;">/*
* Precondition: n has at most one non-null child.
*/</span>
<span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>child <span class="sy0" style="color: rgb(51, 153, 51);">=</span> is_leaf<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">?</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left <span class="sy0" style="color: rgb(51, 153, 51);">:</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
replace_node<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">,</span> child<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>child<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> RED<span class="br0">)</span>
child<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">else</span>
delete_case1<span class="br0">(</span>child<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
<span class="kw3">free</span><span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
如果 N 和它初始的父亲是黑色,则删除它的父亲导致通过 N 的路径都比不通过它的路径少了一个黑色节点。因为这违反了属性 4,树需要被重新平衡。有几种情况需要考虑:
情况 1: N 是新的根。在这种情况下,我们就做完了。我们从所有路径去除了一个黑色节点,而新根是黑色的,所以属性都保持着。
<span class="kw4" style="color: rgb(153, 51, 51);">void</span>
delete_case1<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="kw1">if</span> <span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent <span class="sy0" style="color: rgb(51, 153, 51);">!=</span> NULL<span class="br0">)</span>
delete_case2<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
注意: 在情况2、5和6下,我们假定 N 是它父亲的左儿子。如果它是右儿子,则在这些情况下的左和右应当对调。
|
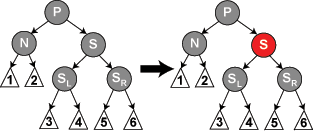
情况 2: S 是红色。在这种情况下我们在N的父亲上做左旋转,把红色兄弟转换成N的祖父。我们接着对调 N 的父亲和祖父的颜色。尽管所有的路径仍然有相同数目的黑色节点,现在 N 有了一个黑色的兄弟和一个红色的父亲,所以我们可以接下去按 4、5或6情况来处理。(它的新兄弟是黑色因为它是红色S的一个儿子。) |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span>
delete_case2<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>s <span class="sy0" style="color: rgb(51, 153, 51);">=</span> sibling<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> RED<span class="br0">)</span> <span class="br0">{</span>
n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> RED<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="br0">)</span>
rotate_left<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">else</span>
rotate_right<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
delete_case3<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
|
情况 3: N 的父亲、S 和 S 的儿子都是黑色的。在这种情况下,我们简单的重绘 S 为红色。结果是通过S的所有路径,它们就是以前不通过 N 的那些路径,都少了一个黑色节点。因为删除 N 的初始的父亲使通过 N 的所有路径少了一个黑色节点,这使事情都平衡了起来。但是,通过 P 的所有路径现在比不通过 P 的路径少了一个黑色节点,所以仍然违反属性4。要修正这个问题,我们要从情况 1 开始,在 P 上做重新平衡处理。 |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span>
delete_case3<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>s <span class="sy0" style="color: rgb(51, 153, 51);">=</span> sibling<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span><span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span><span class="br0">)</span> <span class="br0">{</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> RED<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
delete_case1<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span> <span class="kw1">else</span>
delete_case4<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
|
情况 4: S 和 S 的儿子都是黑色,但是 N 的父亲是红色。在这种情况下,我们简单的交换 N 的兄弟和父亲的颜色。这不影响不通过 N 的路径的黑色节点的数目,但是它在通过 N 的路径上对黑色节点数目增加了一,添补了在这些路径上删除的黑色节点。 |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span>
delete_case4<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>s <span class="sy0" style="color: rgb(51, 153, 51);">=</span> sibling<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span><span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> RED<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span><span class="br0">)</span> <span class="br0">{</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> RED<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span> <span class="kw1">else</span>
delete_case5<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
|
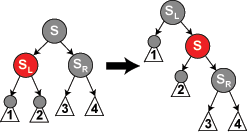
情况 5: S 是黑色,S 的左儿子是红色,S 的右儿子是黑色,而 N 是它父亲的左儿子。在这种情况下我们在 S 上做右旋转,这样 S 的左儿子成为 S 的父亲和 N 的新兄弟。我们接着交换 S 和它的新父亲的颜色。所有路径仍有同样数目的黑色节点,但是现在 N 有了一个右儿子是红色的黑色兄弟,所以我们进入了情况 6。N 和它的父亲都不受这个变换的影响。 |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span>
delete_case5<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>s <span class="sy0" style="color: rgb(51, 153, 51);">=</span> sibling<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="br0">{</span> <span class="coMULTI" style="color: rgb(128, 128, 128); font-style: italic;">/* this if statement is trivial,
due to Case 2 (even though Case two changed the sibling to a sibling's child,
the sibling's child can't be red, since no red parent can have a red child). */</span>
<span class="co1" style="color: rgb(102, 102, 102); font-style: italic;">// the following statements just force the red to be on the left of the left of the parent, </span>
<span class="co1" style="color: rgb(102, 102, 102); font-style: italic;">// or right of the right, so case six will rotate correctly.</span>
<span class="kw1">if</span> <span class="br0">(</span><span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> RED<span class="br0">)</span><span class="br0">)</span> <span class="br0">{</span> <span class="co1" style="color: rgb(102, 102, 102); font-style: italic;">// this last test is trivial too due to cases 2-4.</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> RED<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
rotate_right<span class="br0">(</span>s<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span> <span class="kw1">else</span> <span class="kw1">if</span> <span class="br0">(</span><span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> BLACK<span class="br0">)</span> <span class="sy0" style="color: rgb(51, 153, 51);">&&</span>
<span class="br0">(</span>s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">==</span> RED<span class="br0">)</span><span class="br0">)</span> <span class="br0">{</span><span class="co1" style="color: rgb(102, 102, 102); font-style: italic;">// this last test is trivial too due to cases 2-4.</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> RED<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
rotate_left<span class="br0">(</span>s<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
<span class="br0">}</span>
delete_case6<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
|
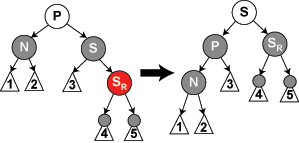
情况 6: S 是黑色,S 的右儿子是红色,而 N 是它父亲的左儿子。在这种情况下我们在 N 的父亲上做左旋转,这样 S 成为 N 的父亲和 S 的右儿子的父亲。我们接着交换 N 的父亲和 S 的颜色,并使 S 的右儿子为黑色。子树在它的根上的仍是同样的颜色,所以属性 3 没有被违反。但是,N 现在增加了一个黑色祖先: 要么 N 的父亲变成黑色,要么它是黑色而 S 被增加为一个黑色祖父。所以,通过 N 的路径都增加了一个黑色节点。 此时,如果一个路径不通过 N,则有两种可能性:
在任何情况下,在这些路径上的黑色节点数目都没有改变。所以我们恢复了属性 4。在示意图中的白色节点可以是红色或黑色,但是在变换前后都必须指定相同的颜色。 |
<span class="kw4" style="color: rgb(153, 51, 51);">void</span>
delete_case6<span class="br0">(</span><span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>n<span class="br0">)</span>
<span class="br0">{</span>
<span class="kw4" style="color: rgb(153, 51, 51);">struct</span> node <span class="sy0" style="color: rgb(51, 153, 51);">*</span>s <span class="sy0" style="color: rgb(51, 153, 51);">=</span> sibling<span class="br0">(</span>n<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="kw1">if</span> <span class="br0">(</span>n <span class="sy0" style="color: rgb(51, 153, 51);">==</span> n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="br0">)</span> <span class="br0">{</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>right<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
rotate_left<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span> <span class="kw1">else</span> <span class="br0">{</span>
s<span class="sy0" style="color: rgb(51, 153, 51);">-></span>left<span class="sy0" style="color: rgb(51, 153, 51);">-></span>color <span class="sy0" style="color: rgb(51, 153, 51);">=</span> BLACK<span class="sy0" style="color: rgb(51, 153, 51);">;</span>
rotate_right<span class="br0">(</span>n<span class="sy0" style="color: rgb(51, 153, 51);">-></span>parent<span class="br0">)</span><span class="sy0" style="color: rgb(51, 153, 51);">;</span>
<span class="br0">}</span>
<span class="br0">}</span>
同样的,函数调用都使用了尾部递归,所以算法是原地算法。此外,在旋转之后不再做递归调用,所以进行了恒定数目(最多 3 次)的旋转。 红黑树是很复杂的数据结构,在一般的情况下是用不到的,仅在大学中提及,在研究生时学到,希望大家能掌握红黑树
渐进边界的证明
包含n个内部节点的红黑树的高度是 O(log(n))。
定义:
- h(v) = 以节点v为根的子树的高度。
- bh(v) = 从v到子树中任何叶子的黑色节点的数目(如果v是黑色则不计数它)(也叫做黑色高度)。
引理: 以节点v为根的子树有至少 个内部节点。
个内部节点。
引理的证明(通过归纳高度):
基础: h(v) = 0
如果v的高度是零则它必定是 nil,因此 bh(v) = 0。所以:

归纳假设: h(v) = k 的v有 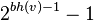 个内部节点暗示了 h(
个内部节点暗示了 h(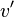 ) = k+1 的
) = k+1 的 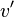 有
有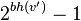 个内部节点。
个内部节点。
因为 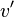 有 h(
有 h(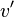 ) > 0 所以它是个内部节点。同样的它有黑色高度要么是 bh(
) > 0 所以它是个内部节点。同样的它有黑色高度要么是 bh(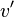 ) 要么是 bh(
) 要么是 bh(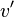 )-1 (依据
)-1 (依据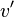 是红色还是黑色)的两个儿子。通过归纳假设每个儿子都有至少
是红色还是黑色)的两个儿子。通过归纳假设每个儿子都有至少 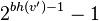 个内部接点,所以
个内部接点,所以 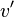 有:
有:

个内部节点。
使用这个引理我们现在可以展示出树的高度是对数性的。因为在从根到叶子的任何路径上至少有一半的节点是黑色(根据红黑树属性4),根的黑色高度至少是h(root)/2。通过引理我们得到:

因此根的高度是O(log(n))。
参见
注释
- ^ 性质1. 节点是红色或黑色。
- ^ 性质3. 所有叶子都是黑色。
- ^ 3.0 3.1 3.2 3.3 3.4 性质4. 每个红色节点的两个子节点都是黑色。
- ^ 4.0 4.1 4.2 4.3 4.4 4.5 性质5. 从每个叶子到根的所有路径都包含相同数目的黑色节点。
- ^ 性质2. 根是黑色。
引用
- Mathworld: Red-Black Tree
- San Diego State University: CS 660: Red-Black tree notes, by Roger Whitney
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms. Massachusetts: The MIT Press, 2002. pp273-77. ISBN 0-07-013151-1
外部链接
- An applet + quick explanation
- Red/Black Tree Demonstration
- An example (animated GIF, 200KB)
- An example (static picture)
- Another explanation (pictures, source code, and Java interactive animation)
- Red-Black Tree Demonstration by David M. Howard
- RBT: A SmallEiffel Red-Black Tree Library
- libredblack: A C Red-Black Tree Library
- Red-Black Tree C++ Code
- Red-Black Trees by Thomas Niemann
- 红黑树的介绍和实现



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








