字典树(Tire树)

引:假如有n(n很大)个字符串，有q个查询，每个查询表示在这n个串里面是否存在这个要查询的串。一种方法就是直接暴力查找，但是复杂度很高，稍微优化一点的方法是先把n个串排序，然后二分查找，但复杂度仍可以优化，hash或者字典树都可以，这里介绍字典树。

字典树是一颗树，每个节点都有多个子节点，子节点的数量取决于字符的范围，比如如果只有小写字母子节点就有26个就足够了，例如对于这六个字符串:ab, ada, bfg, ehn, eb, adp所构成的字典树如下：

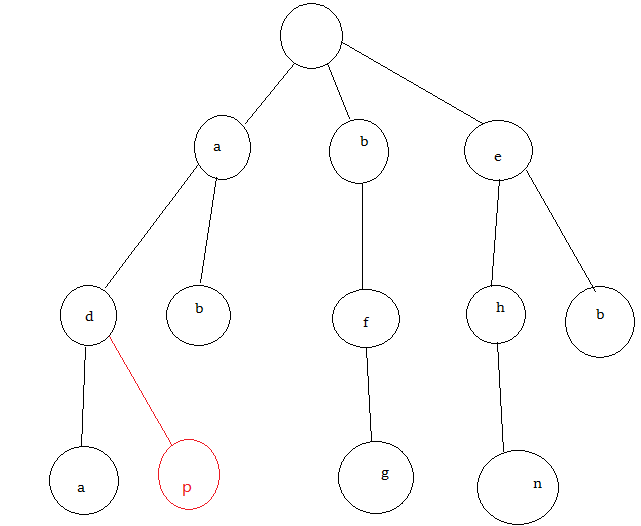
注意红色部分是字典树的精华，对于ada和adp这两个字符串相同的前缀不会重复保存，即字典树不会重复保存没用的字符。
每个节点有些空节点就不画出来了，这里限制字符仅有小写字母，即每个节点有26个子节点，下标对应为0:a, 1:b, 2:c…………..

const int tp = 27;   ///字符范围
struct node {
    char val;     /// 当前节点的字符
    bool ifc;     ///  这个节点是否是字符串的结束位置
    struct node *next[tp];  ///子节点
} *root;  /// root是字典树的根节点

然后首先需要把n个字符串全部加入到字典树中才能够进行查询，插入操作很简单，只需要顺着树进行就可以了。

node* getNewNode() {   ///生成新节点
    node *p = new node;
    for (int i = 0; i < tp; ++i) p->next[i] = NULL;
    p->val = 0;
    p->ifc = false;
}

void Insert(char *str) {
    node *p = root;  ///注意不要直接操作根节点
    for (int i = 0; i < strlen(str); ++i) {
        int tmp = str[i] - 'a';   ///获取下标
        if (!p->next[tmp]) p->next[tmp] = getNewNode(); ///如果该节点为空则需要新建节点来延伸字典树
        p = p->next[tmp];   ///传递到下一节点
    }
    p->ifc = true;  ///注意在结束位置打上标记
}

然后剩下的查找标记只需要顺着根节点来一步一步往下走就可以了

bool Find(char *str) {
    node *rt = root;  ///注意不要直接操作根节点
    for (int i = 0; i < strlen(str); ++i) {
        int tmp = str[i] - 'a';
        if (rt->next[tmp]) rt = rt->next[tmp];
        else return false;
    }
    return rt->ifc;
}

附总代码:

#include <bits/stdc++.h>

using namespace std;

const int maxn = 1000 + 7;
const int INF = ~0U >> 1;
const int tp = 27;

typedef long long LL;

struct node {
    char val;
    bool ifc;
    struct node *next[tp];
} *root;

char s[maxn];
int n, q;

node* getNewNode() {
    node *p = new node;
    for (int i = 0; i < tp; ++i) p->next[i] = NULL;
    p->val = 0;
    p->ifc = false;
}

void Insert(char *str) {
    node *p = root;
    for (int i = 0; i < strlen(str); ++i) {
        int tmp = str[i] - 'a';
        if (!p->next[tmp]) p->next[tmp] = getNewNode();
        p = p->next[tmp];
    }
    p->ifc = true;
}

void Delete(node *rt) {
    for (int i = 0; i < tp; ++i)
        if (rt->next[i]) Delete(rt->next[i]);
    delete rt;
}

bool Find(char *str) {
    node *rt = root;
    for (int i = 0; i < strlen(str); ++i) {
        int tmp = str[i] - 'a';
        if (rt->next[tmp]) rt = rt->next[tmp];
        else return false;
    }
    return rt->ifc;
}

int main() {
    root = getNewNode();
    scanf("%d%d", &n, &q);
    for (int i = 0; i < n; ++i) {
        scanf("%s", s);
        Insert(s);
    }
    for (int i = 0; i < q; ++i) {
        scanf("%s", s);
        if (Find(s)) printf("YES\n");
        else printf("NO\n");
    }
    Delete(root);
    return 0;
}

在字符集很大的情况下就不能用上述这种方式进行建树了，会爆内存。这里介绍一个字典树的另一种写法，写的比较挫，见谅。
左儿子右兄弟的写法，即lc指针指的是这个节点的儿子指针，rc指的是这个节点的兄弟节点。
如图:

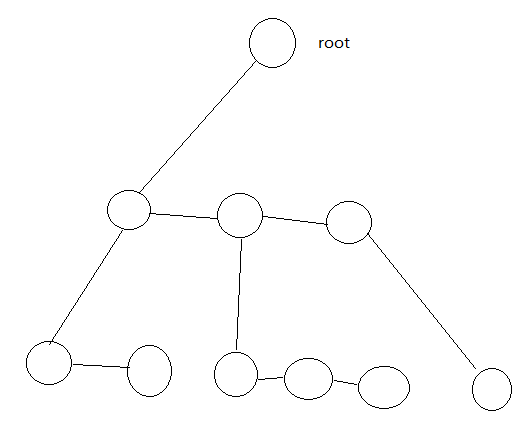
图做的有点low。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cstdlib>

using namespace std;

const int maxn = 100 + 7;

struct node {
    struct node *lc, *rc;
    bool ifc;
    char ch;
};

struct node *root;
int flag[maxn];

node *getNewNode() {
    struct node *q = new node;
    q->ifc = false;
    q->lc = q->rc = NULL;
    return q;
}

void Insert(char *s) {
    int len = strlen(s);
    struct node *p = root;
    for (int i = 0; i < len; ++i) {
        struct node *q, *tmp;
        bool ok = false;
        for (q = p->lc; q; q = q->rc) {
            if (q->rc == NULL) tmp = q;
            if (q->ch == s[i]) {
                ok = true;
                break;
            }
        }
        if (!ok) {
            if (q == p->lc) {
                q = getNewNode();
                q->ch = s[i];
                p->lc = q;
            } else {
                q = getNewNode();
                q->ch = s[i];
                tmp->rc = q;
            }
        }
        p = q;
    }
    p->ifc = true;
}

bool Find(char *s) {
    int len = strlen(s);
    struct node *p = root;
    for (int i = 0; i < len; ++i) {
        bool ok = false;
        node *q;
        for (q = p->lc; q; q = q->rc)
            if (q->ch == s[i]) {
                ok = true;
                break;
            }
        if (!ok) return false;
        p = q;
    }
    return p->ifc;
}

int n, m;
char str[maxn];

int main() {
    root = new node;
    root->ifc = false;
    root->lc = root->rc = NULL;
    root->ch = 0;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i) {
        scanf("%s", str);
        Insert(str);
    }
    for (int i = 0; i < m; ++i) {
        scanf("%s", str);
        printf("%s\n", Find(str) ? "YES" : "NO");
    }
    return 0;
}