Description
数轴1~n每点有一个骑士,每个骑士有个初始方向di(0表示向右,1表示向左1),骑士单位时间移动单位长度,两个骑士相遇会决斗,每个骑士赢的概率是0.5,输的骑士挂掉,骑士到达0和n+1时会改变方向,问最后活下来的那位骑士是第n位骑士的概率
Input
第一行一整数T表示用例组数,每组用例首先输入一整数b表示骑士数量,之后n个01表示每个骑士的初始方向(T<=10,1<=n<=1000)
Output
对于每组用例,输出最后活下来的那位骑士是第n位骑士的概率,结果模1e9+7
Sample Input
2
2
0 0
3
0 1 0
Sample Output
Case #1: 500000004
Case #2: 250000002
Solution
第一个骑士往右走,第n个骑士往左走,第n个骑士活下来的情况就是他打败了他左边所有往右走的骑士,令dp[i][j]表示第i名骑士往右走且前i名骑士中有j名骑士方向向右的概率,那么有以下转移方程
若第i名骑士方向向右,那么有dp[i][j]=dp[i-1][j-1]
若第i名骑士方向向左,设前i-1个骑士中k个骑士方向向右,考虑这个骑士往左走打败k-j个骑士后被干掉,那么有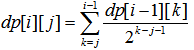
注意到j=1时有两种情况,一种是第i名骑士干掉前面一些方向向右的骑士后被最后一个向右的骑士干掉,另一种是第i名骑士干掉前面所有向右的骑士后到0点改变方向,故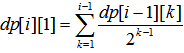
进一步优化这个转移方程有
dp[i][1]=dp[i-1][1]+dp[i][2]
dp[i][j]=(dp[i-1][j]+dp[i][j+1])/2,j=2,3,..,i-1
最后答案就是dp[n][1]/2,除以2是因为最后向右的必须是第n个骑士,也就是说第n个骑士与其左边最后一个骑士决斗要胜出,而不是被打败
Code
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
#define mod 1000000007ll
#define inv2 500000004ll
#define maxn 1111
ll dp[maxn][maxn];
int T,n,d,Case=1;
int main()
{
scanf("%d",&T);
while(T--)
{
printf("Case #%d: ",Case++);
scanf("%d",&n);
memset(dp,0,sizeof(dp));
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
scanf("%d",&d);
if(i==1)d=1;
if(i==n)d=0;
if(d)
{
for(int j=1;j<=i;j++)
dp[i][j]=dp[i-1][j-1];
}
else
{
for(int j=i-1;j>1;j--)
dp[i][j]=(dp[i-1][j]+dp[i][j+1])%mod*inv2%mod;
dp[i][1]=(dp[i-1][1]+dp[i][2])%mod;
}
}
printf("%I64d\n",dp[n][1]*inv2%mod);
}
return 0;
}























 828
828

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








