HDU 5868 Different Circle Permutation（dp+polya+矩阵快速幂+欧拉函数）

Description
环上均匀分布n个点，每个点可以坐人和不坐人，相邻两点不能同时坐人，旋转后相等视为同一种方案，问有多少种方案
Input
多组用例，每组用例输入一个整数n，以文件尾结束输入
(不超过50组用例，1<=n<=1e9)
Output
对于每组用例，输出合法方案数
Sample Input
4
7
10
Sample Output
3
5
15
Solution
问题为从环上的n个点中选一些点染色，相邻两点不能同时染色
先不考虑旋转同构，用g[i]表示在不考虑旋转同构的前提下给i个点的环染色的合法方案数，先考虑一条链上的情况，用dp[i][0]表示第i个点不染色的方案数，dp[i][1]表示第i个点染色的方案数，那么由以下转移方程：
dp[1][0]=dp[1][1]=1
dp[i][0]=dp[i-1][0]+dp[i-1][1]，dp[i][1]=dp[i-1][0]，i=2,3,…,n
显然可以发现dp[i][0]是斐波那契数列的第i+1项，考虑第n个点是否染色，如果不染色那么可以将这个链连成一个环，方案数dp[n][0]；如果染色，那么第1个点必然不染，而从第2个点开始到第n个点还是可以看做一条链上的染色，方案数dp[n-1][1]=dp[n-2][0]
故有g[n]=f[n-1]+f[n+1]，f[i]表示斐波那契数列第i项，进一步由f[i]=f[i-1]+f[i-2]知g[i]=g[i-1]+g[i-2]，其中g[1]=1,g[2]=3
之后考虑旋转，由Burnside引理知合法方案数

枚举d，矩阵快速幂O(logn)求g，求一个数的欧拉函数也是O(logn)，故总时间复杂度
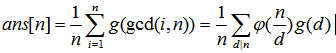
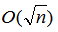
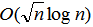
注意n=1时特判答案是2，因为一个人的时候第1个人和第n个人可以同时染色
Code

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
#define mod 1000000007ll 
typedef long long ll;
struct Mat
{
    ll mat[3][3];//矩阵 
    int row,col;//矩阵行列数 
};
Mat mod_mul(Mat a,Mat b,int p)//矩阵乘法 
{
    Mat ans;
    ans.row=a.row;
    ans.col=b.col;
    memset(ans.mat,0,sizeof(ans.mat));
    for(int i=0;i<ans.row;i++)      
        for(int k=0;k<a.col;k++)
            if(a.mat[i][k])
                for(int j=0;j<ans.col;j++)
                {
                    ans.mat[i][j]+=a.mat[i][k]*b.mat[k][j]%p;
                    ans.mat[i][j]%=p;
                }
    return ans;
}
Mat mod_pow(Mat a,int k,int p)//矩阵快速幂 
{
    Mat ans;
    ans.row=a.row;
    ans.col=a.col;
    for(int i=0;i<a.row;i++)
        for(int j=0;j<a.col;j++)
            ans.mat[i][j]=(i==j);
    while(k)
    {
        if(k&1)ans=mod_mul(ans,a,p);
        a=mod_mul(a,a,p);
        k>>=1;
    }
    return ans;
}
#define maxn 55555
int euler[maxn],prime[maxn],res;
void Get_euler(int n)//求n以内所有数的欧拉函数值,顺便得到n以内所有素数共res个
{
    memset(euler,0,sizeof(euler));
    euler[1]=1;
    res=0;
    for(int i=2;i<=n;i++)
    {
        if(!euler[i])euler[i]=i-1,prime[res++]=i;
        for(int j=0;j<res&&prime[j]*i<=n;j++)
        {
            if(i%prime[j]) euler[prime[j]*i]=euler[i]*(prime[j]-1);
            else
            {
                euler[prime[j]*i]=euler[i]*prime[j];
                break;
            }
        }
    }
}
ll f[maxn];
void init()
{
    Get_euler(50000);
    f[1]=1,f[2]=3;
    for(int i=3;i<=50000;i++)f[i]=(f[i-1]+f[i-2])%mod;
}
ll get_f(int n)
{
    if(n<=50000)return f[n];
    Mat A;
    A.row=A.col=2;
    A.mat[0][0]=1,A.mat[0][1]=1,
    A.mat[1][0]=1,A.mat[1][1]=0;
    A=mod_pow(A,n-2,mod);
    return 3ll*A.mat[0][0]+A.mat[0][1];
}
ll get_euler(int n)
{
    if(n<=50000)return euler[n];
    ll ans=n;
    for(int i=2;i*i<=n;i++)
        if(n%i==0)
        {
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}
ll Mod_pow(ll a,ll b)
{
    a%=mod;
    ll ans=1ll;
    while(b)
    {
        if(b&1)ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}
int main()
{
    init();
    int n;
    while(~scanf("%d",&n))
    {
        if(n==1)
        {
            printf("2\n");
            continue;
        }
        ll ans=0;
        for(int i=1;i*i<=n;i++)
            if(n%i==0)
            {
                ll temp=(get_f(i))%mod*get_euler(n/i)%mod;
                ans=(ans+temp)%mod;
                if(i*i!=n)
                {
                    int j=n/i;
                    temp=get_f(j)*get_euler(n/j)%mod;
                    ans=(ans+temp)%mod;
                }           
            }
        printf("%I64d\n",ans*Mod_pow(n,mod-2)%mod);
    }
    return 0;
}