[替罪羊树] BZOJ 3224

最新推荐文章于 2022-06-21 10:10:35 发布

Vectorxj

最新推荐文章于 2022-06-21 10:10:35 发布

阅读量588

点赞数 1

分类专栏：平衡树文章标签：数据结构替罪羊树二叉搜索树

本文链接：https://blog.csdn.net/Vectorxj/article/details/51537740

版权

平衡树专栏收录该内容

5 篇文章 0 订阅

订阅专栏

3224: Tyvj 1728 普通平衡树
Description
您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：
1. 插入x数
2. 删除x数(若有多个相同的数，因只删除一个)
3. 查询x数的排名(若有多个相同的数，因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x，且最大的数)
6. 求x的后继(后继定义为大于x，且最小的数)
Input
第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号(1<=opt<=6)
Output
对于操作3,4,5,6每行输出一个数，表示对应答案
Sample Input
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
Sample Output
106465
84185
492737
HINT
1.n的数据范围：n<=100000
2.每个数的数据范围：[-1e7,1e7]
Source
平衡树

这题应该有很多解法。Treap，红黑树，AVL树等等等。反正需要一颗平衡二叉树。
Treap已经打过很多遍了，这次就选择了替罪羊树。那么先讲一讲替罪羊树。
说得通俗一些，替罪羊树就是找到一颗不平衡子树将其拍平，再从中点将其提起来，那么很显然这一操作（重构）之后依旧是一颗二叉搜索树，且十分平衡，大概是这样的。

比如有这么一棵子树
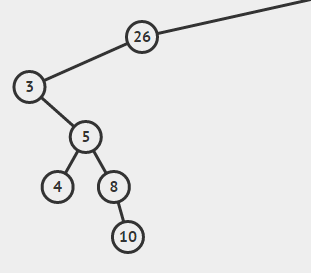
这里写图片描述
只要中序遍历一遍，就得到了一个序列

把它从中间提起，就能够形成一颗较平衡的二叉搜索树啦

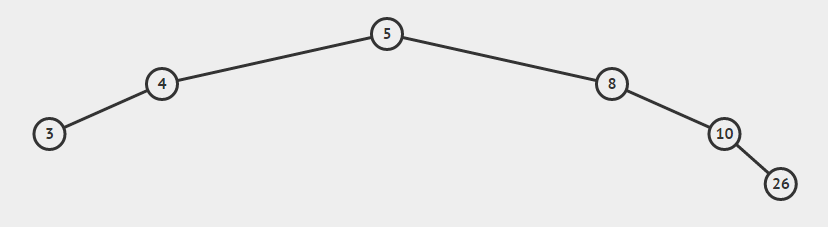
这就是整个维护的过程，那么什么时候要维护呢

  const double alpha = 0.75;

  inline bool IsBad(void) {
    return ((ch[0]->cover > cover * alpha + 5)
      || (ch[1]->cover > cover * alpha + 5));
  }

至于这个为什么是0.75呢作者现在还太傻不会。。。。。
插入之后要找到离根节点最近的需要重构的地方，重构即可。
删除不会删除该节点，而是把它看成是不存在的。所以每次重构时如果该点存在，加入序列，否则放到垃圾回收站中，这样这个节点的地址可以重复使用。
其他操作和普通二叉树差不多。

 void Travel(node *o, vector<node*> &v) {
    if (o == null) return;
    Travel(o->ch[0], v);
    if (o->IsExistent) v.push_back(o);
    else rubbish[rublen++] = o;
    Travel(o->ch[1], v);
  }
  node* New(const vector<node*> &v, int L, int R) {
    if (L >= R) return null;
    int Mid = (L + R) >> 1;
    node *o = v[Mid];
    o->ch[0] = New(v, L, Mid);
    o->ch[1] = New(v, Mid + 1, R);
    o->maintain();
    return o;
  }
  void Rebuild(node* &o) {
    V.clear();
    Travel(o, V); o = New(V, 0, V.size());
  }

删除我写了三个。好像都差不多


  void Erase(node* &o, int x) {//按键值删除
    if (flag || o == null) return;
    if (o->key == x && o->IsExistent) {
      o->IsExistent = 0; o->maintain();
      flag = 1; return;
    }
    if (o->key == x) Erase(o->ch[0], x);
    Erase(o->ch[x >= o->key], x);
    o->maintain();
  }
  void _Erase(node* &o, int id) {//按排名删除
    int size = o->ch[0]->size + o->IsExistent;
    if (o == null) return;
    if (o->IsExistent && size == id) {
        o->IsExistent = 0; o->maintain();
        return;
    }
    if (id <= size) _Erase(o->ch[0], id);
    else _Erase(o->ch[1], id - size);
    o->maintain();
  }
  void __Erase(node* &o, int id) {//按排名删除，非递归
    int size; node* p = o;
    while (p != null) {
      size = p->ch[0]->size + p->IsExistent;
      p->size--;
      if (p->IsExistent && id == size) {
        p->IsExistent = 0; return ;
      }
      if (id <= size) {
        p = p->ch[0];
      } else {
        p = p->ch[1]; id -= size;
      }
    }
  }

大概就是这样啦。这道题的话直接套模板即可。

附代码：

#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;

namespace ScapeGoatTree {

#define N 100100

const double alpha = 0.75;
struct node {
  node *ch[2];
  int size, cover, key;
  bool IsExistent;
  inline bool IsBad(void) {
    return ((ch[0]->cover > cover * alpha + 5)
      || (ch[1]->cover > cover * alpha + 5));
  }
  inline void maintain(void) {
    cover = ch[0]->cover + ch[1]->cover;
    size = ch[0]->size + ch[1]->size + IsExistent;
  }
};
struct Tree {
protected:
  node *root, *null, *ToMem;
  node mem[N], *rubbish[N];
  vector<node*> V;
  int rublen;
  bool flag;
  inline node* NewNode(int x) {
    node* o = rublen ? rubbish[--rublen] : ToMem++;
    o->ch[0] = o->ch[1] = null;
    o->size = o->cover = 1;
    o->key = x; o->IsExistent = 1;
    return o;
  }
  void Travel(node *o, vector<node*> &v) {
    if (o == null) return;
    Travel(o->ch[0], v);
    if (o->IsExistent) v.push_back(o);
    else rubbish[rublen++] = o;
    Travel(o->ch[1], v);
  }
  node* New(const vector<node*> &v, int L, int R) {
    if (L >= R) return null;
    int Mid = (L + R) >> 1;
    node *o = v[Mid];
    o->ch[0] = New(v, L, Mid);
    o->ch[1] = New(v, Mid + 1, R);
    o->maintain();
    return o;
  }
  void Rebuild(node* &o) {
    V.clear();
    Travel(o, V); o = New(V, 0, V.size());
  }
  node** Insert(node* &o, int x) {
    if (o == null) {
      o = NewNode(x); return &o;
    }
    node** p = Insert(o->ch[x >= o->key], x);
    o->maintain();
    if (o->IsBad()) p = &o;
    return p;
  }
  void Erase(node* &o, int x) {
    if (flag || o == null) return;//flag以防多删节点
    if (o->key == x && o->IsExistent) {
      o->IsExistent = 0; o->maintain();
      flag = 1; return;
    }
    if (o->key == x) Erase(o->ch[0], x);
    Erase(o->ch[x >= o->key], x);
    o->maintain();
  }
  void _Erase(node* &o, int id) {
    int size = o->ch[0]->size + o->IsExistent;
    if (o == null) return;
    if (o->IsExistent && size == id) {
        o->IsExistent = 0; o->maintain();
        return;
    }
    if (id <= size) _Erase(o->ch[0], id);
    else _Erase(o->ch[1], id - size);
    o->maintain();
  }
  void __Erase(node* &o, int id) {
    int size; node* p = o;
    while (p != null) {
      size = p->ch[0]->size + p->IsExistent;
      p->size--;
      if (p->IsExistent && id == size) {
        p->IsExistent = 0; return ;
      }
      if (id <= size) {
        p = p->ch[0];
      } else {
        p = p->ch[1]; id -= size;
      }
    }
  }
public:
  void Initial(void) {
    ToMem = mem; null = ToMem++;
    null->ch[0] = null->ch[1] = null;
    null->size = null->cover = 0;
    root = null; rublen = 0;
  }
  Tree(void) {Initial();}
  void Insert(int x) {
    node** o = Insert(root, x);
    if (*o != null) Rebuild(*o);
  }
  int Rank(int x) {
    int ans = 1; node* o = root;
    while (o != null) {
      if (x <= o->key) {
        o = o->ch[0];
      } else {
        ans += o->ch[0]->size + o->IsExistent;
        o = o->ch[1];
      }
    }
    return ans;
  }
  int Kth(int k) {
    node* o = root;
    while (o != null) {
      if (k == o->ch[0]->size + 1 && o->IsExistent) return o->key;
      if (k <= o->ch[0]->size) {
        o = o->ch[0];
      } else {
        k -= o->ch[0]->size + o->IsExistent;
        o = o->ch[1];
      }
    }
  }
  void Erase(int x) {
//    flag = 0; Erase(root, x);
    __Erase(root, Rank(x));
    if (root->size < alpha * root->cover) Rebuild(root);
  }
};

#undef N

}

inline char get(void) {
  static char buf[1000000], *p1 = buf, *p2 = buf;
  if (p1 == p2) {
    p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin);
    if (p1 == p2) return EOF;
  }
  return *p1++;
}
inline void read(int &x) {
  x = 0; char c = get(); int sign = 1;
  for (; c < '0' || c > '9'; c = get()) if(c == '-') sign = 0;
  for (; c >= '0' && c <= '9'; x = (x << 1) + (x << 3) + c - '0', c = get());
  x = sign ? x : -x;
}

using namespace ScapeGoatTree;
Tree solution;
int n, x, p;

int main(void) {
  freopen("3224.in", "r", stdin);
  freopen("3224.out", "w", stdout);
  read(n);
  for (int i = 0; i < n; i++) {
    read(x); read(p);
    switch (x) {
      case 1: solution.Insert(p); break;
      case 2: solution.Erase(p); break;
      case 3: printf("%d\n", solution.Rank(p)); break;
      case 4: printf("%d\n", solution.Kth(p)); break;
      case 5: printf("%d\n", solution.Kth(solution.Rank(p) - 1)); break;
      case 6: printf("%d\n", solution.Kth(solution.Rank(p + 1))); break;
    }
  }
  fclose(stdin); fclose(stdout);
  return 0;
}

Vectorxj

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
[替罪羊树] BZOJ 3224

3224: Tyvj 1728 普通平衡树 Description 您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作： 1. 插入x数 2. 删除x数(若有多个相同的数，因只删除一个) 3. 查询x数的排名(若有多个相同的数，因输出最小的排名) 4. 查询排名为x的数 5. 求x的前驱(前驱定义为小于x，且最大的数) 6. 求x的后继(后继定义为大于x，且最
复制链接

扫一扫