单源最短路径 Bellman_Ford

一、问题简述
Dijkstra算法无法判断含负权边的图的最短路。如果遇到负权，在没有负权回路（回路的权值和为负，即便有负权的边）存在时，也可以采用Bellman - Ford算法正确求出最短路径。
Bellman-Ford算法能在更普遍的情况下（存在负权边）解决单源点最短路径问题。对于给定的带权（有向或无向）图 G=(V,E), 其源点为v0。
接下来分析回路问题，如果有正回路，则动态规划会因为松弛操作选出最优答案，必然是不会走重复回路的，那么n-1个节点就能找到再也无法松弛的结果，无须担心。但是如果是负回路，那么步数越多，则距离越小，所以对最后结果再进行松弛操作，也是可以找到答案的。
如果不存在这样的负回路，算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
附：松弛操作

二、算法思想
首先：初始化邻接矩阵
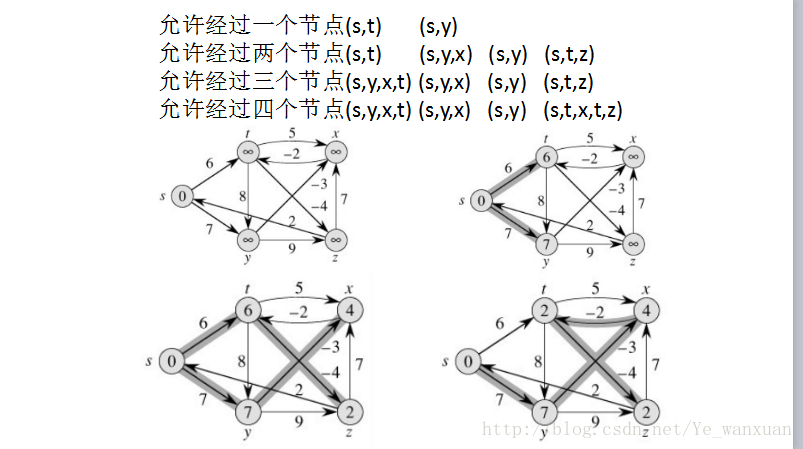
其次：进行不断的松弛操作（bellman函数）

另外：再把每次松弛时把每条边都更新一下，若在n-1次松弛后还能更新，则说明图中有负环，因此无法得出结果（minus函数）。
最后：path函数去寻找路径

三、具体代码

#include <iostream>
#include<stack>
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<queue>
#include<climits>
#include<cstring>
using namespace std;
struct node0
{
    int kdist;
    int dist;
    int path;
};
int i,j,k;
int bellman( int **graph,n