【线性代数公开课MIT Linear Algebra】 第二十二课 特征分解与矩阵的幂

本系列笔记为方便日后自己查阅而写，更多的是个人见解，也算一种学习的复习与总结，望善始善终吧~

特征分解 $A=S\Lambda S^{-1}$

$S$由特征向量组成，要求这些特征向量线性无关，这样$S$才可逆，首先:

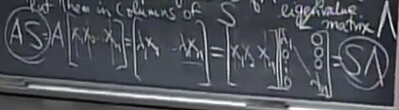
现在我们知道
$AS=S\Lambda$
$\Rightarrow S^{-1}AS=\Lambda$
$\Rightarrow A=S\Lambda S^{-1}$
这就是特征分解Eigen decomposition

矩阵的幂

$Ax=\lambda x$$\Rightarrow A^2x=\lambda Ax=\lambda^2x$
从特征分解角度看
$A^2=S\Lambda S^{-1}S\Lambda S^{-1}=S\Lambda^2 S^{-1}$
$\Rightarrow A^k=S\Lambda^k S^{-1}$
这就是特征分解Eigen decomposition的一大用处

可对角化diagonalizable

当矩阵A没有重复的特征值，矩阵A必有n个线性无关的特征向量，则称A可以对角化diagonalizable

如果存在重复的特征值，那么我们就需要做额外的检查，就是说上面的条件是充分非必要条件。
我们重点关注可对角化的情况，

一阶差分方程组

上面就是一阶差分方程的解，我们想要知道更精确的结果，把$u_0$展开成特征向量的线性组合，则

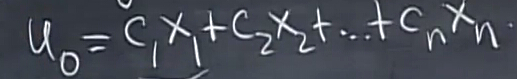
那么

斐波拉契数列 Fibonacci number

对于斐波拉契数列:$a_0=0,a_1=1,a_n=a_{n-1}+a_{n-2}$
$a_n=a_{n-1}+a_{n-2}$这就像一个二阶微分方程，我们需要一些技巧把他化简为一阶微分方程：

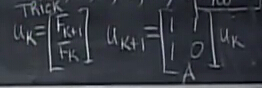
不用想啦，直接特征分解

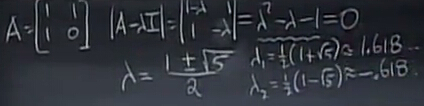
得到两个特征值，那么斐波拉契数列第100个数大约是多少？斐波拉契数列的增长率是怎么样的？

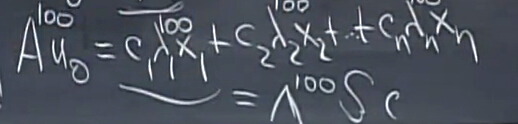
回顾之前的内容，$\lambda_1$为1.618，$\lambda_2$为-0.618，$\lambda_2$随着幂的增加会越来越小，最终趋于0，即增长率主要受$\lambda_1$控制，幂越大，就越接近。
对于微分方程，我们关注的是增长率，即最终到底是发散还是收敛，而这些性质都藏在特征值里面。

PS：另一位仁兄的笔记
http://blog.csdn.net/suqier1314520/article/details/14004579