树链剖分理解&&poj 3237

最新推荐文章于 2023-07-07 07:18:42 发布

兔衰

最新推荐文章于 2023-07-07 07:18:42 发布

阅读量632

点赞数 1

分类专栏： acm_数据结构文章标签：树链剖分 poj3237

本文链接：https://blog.csdn.net/a915800048/article/details/50332885

版权

acm_数据结构专栏收录该内容

17 篇文章 0 订阅

订阅专栏

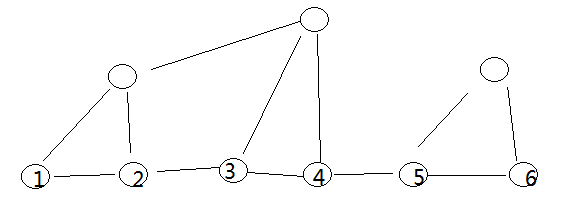
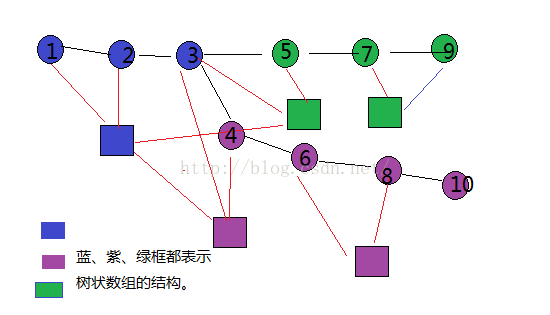
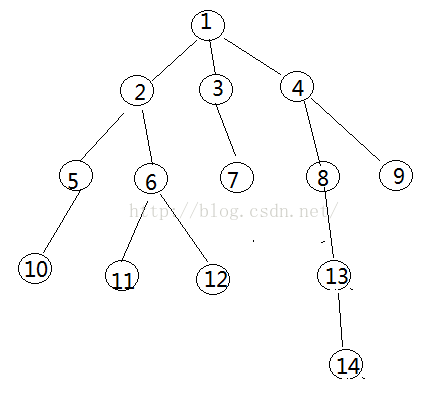
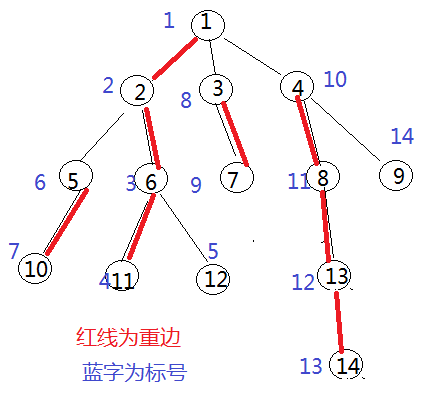
树链剖分用一句话概括就是：把一棵树剖分为若干条链，然后利用数据结构(树状数组，SBT，Splay，线段树等等)去维护每一

条链，复杂度为O(logn)

假如一个树就是一条链的话（极限的想想），我们可以用数据结构（线段树，树桩数组）去维护它。

下图 1-6就是一个链树，用树状数组维护

这个性质很好，维护很方便

然后再画个树，咱们强行用树状数组维护

可以发现，树状数组在3节点后产生了增殖，且1-3节点的树状数组里的值与（5，7,9）、（4,6,8,10）是共有的。也就是说树根的值（映射到树状数组中）影响它的子树。

用树状数组强行维护显然是难办的。因为树状数组对标号的要求是连续。

这个感觉暂且保留。

不要着急，来看看这个。

先上个图

咱们先按搜索序来遍历一下，并在搜索过程中进行标号

节点 : 1 2 5 10 6 11 12 3 7 4 8 13 14 9

标号：1 2 3 4 5 6 7 8 9 10 11 12 13 14

可以发现：（1）父节点总是比它的子孙节点的标号小（因为搜索先对的当前节点标号，继续搜索当前节点的子树是，标号只增不减）

（2）任意树的子孙节点标号区间是连续的（如树根为2的子树）

等等，揪得马得。通过搜索序标号处理，就把每个子树划分成了一个标号连续的区间。连续，就可以用树状数组进行区间维护了。

假设已经用树状数组强行维护了

从两个方面考虑：

（1）更新：一个点u的值更新了，我们要修改的区间就是[p[u],p[u]+size[u]] （说明下，p[u]表示点u的搜索标号，size[u]表示根为u的树的节点个数。之前提过，树根的值影响它的子树，那么映射到树状数组里，就是节点标号连续的区间）。这个需要好好体会下。

（2）查找假如我们要查找从1到11这条链。对应要整合的树状数组的区间就是[1,2]+[5,6]。可以发现查找的区间是几段区间整合起来的。那么查找的次数=树状数组的查询运算次数* 查找一条链需要整合区间的数量 :log(n)*? 。

其实到这里，我们已经解决了用数据结构维护树的问题。但是查找一条链需要整合区间的数量并不确定。

因为这个受搜索序的影响，那么我们就要找到一种搜索序，使平均下来的查找一条链需要整合区间的数量尽可能小。

这个时候就引入树链剖分的原理了。

耐心点看看。

那么，树链剖分的第一步当然是对树进行轻重边的划分。

定义size(x)为以x为根的子树节点个数，令v为u的儿子中size值最大的节点，那么(u,v)就是重边，其余边为轻边。

当然，剖分过程分为两次dfs，或者bfs也可以。

如果是两次dfs，那么第一次dfs就是找重边，也就是记录下所有的重边。

然后第二次dfs就是连接重边形成重链，具体过程就是：以根节点为起点，沿着重边向下拓展，拉成重链，不在当前重链上的节

点，都以该节点为起点向下重新拉一条重链。

剖分完毕后，每条重链相当于一段区间，然后用数据结构去维护，把所有重链首尾相接，放到数据结构上，然后维护整体（耐心，这句不理解继续往下看）。

在这里，当然有很多数组，现在我来分别介绍它们的作用：

siz[]数组，用来保存以x为根的子树节点个数

top[]数组，用来保存当前节点的所在链的顶端节点

son[]数组，用来保存重儿子

dep[]数组，用来保存当前节点的深度

fa[]数组，用来保存当前节点的父亲

tid[]数组，用来保存树中每个节点剖分后的新编号

rank[]数组，用来保存当前节点在线段树中的位置

那么，我们现在可以根据描述给出剖分的代码：

第一次dfs：记录所有的重边

void dfs1(int u,int father,int d)  
{  
    dep[u]=d;  
    fa[u]=father;  
    siz[u]=1;  
    for(int i=head[u];~i;i=next[i])  
    {  
        int v=to[i];  
        if(v!=father)  
        {  
            dfs1(v,u,d+1);  
            siz[u]+=siz[v];  
            if(son[u]==-1||siz[v]>siz[son[u]])  
                son[u]=v;  
        }  
    }  
}

第二次dfs：连重边成重链，重儿子优先进行搜索（也就是说重边链接的树优先编号）。

void dfs2(int u,int tp)  
{  
    top[u]=tp;  
    tid[u]=++tim;  
    rank[tid[u]]=u;  
    if(son[u]==-1) return;  
    dfs2(son[u],tp);  
    for(int i=head[u];~i;i=next[i])  
    {  
        int v=to[i];  
        if(v!=son[u]&&v!=fa[u])  
            dfs2(v,v);  
    }  
}

还是上面那个树，我们画个剖分后的图：

可以发现重链上的标号，TMD居然是连续的。也就是说每条重链就对应的就是一段连续的区间。

当然，关于这个它有两个重要的性质：

(1)轻边(u,v)中，size(v)<=size(u/2)

(2)从根到某一点的路径上，不超过logn条轻边和不超过logn条重路径。

每条重链上标号是连续的，轻边链接的两个节点标号绝对不连续。由性质（2），能推出，每次查找一条链需要整合区间的数量不超过log(n)

那么总的查找效率就(log(n))^2.

引用博客：http://www.2cto.com/kf/201308/240268.html

理解完了，那就来A道题：poj 3237 Tree

Tree

Time Limit: 5000MS		Memory Limit: 131072K
Total Submissions: 6981		Accepted: 1913

Description

You are given a tree with N nodes. The tree’s nodes are numbered 1 through N and its edges are numbered 1 through N − 1. Each edge is associated with a weight. Then you are to execute a series of instructions on the tree. The instructions can be one of the following forms:

`CHANGE` i v	Change the weight of the ith edge to v
`NEGATE` a b	Negate the weight of every edge on the path from a to b
`QUERY` a b	Find the maximum weight of edges on the path from a to b

Input

The input contains multiple test cases. The first line of input contains an integer t (t ≤ 20), the number of test cases. Then follow the test cases.

Each test case is preceded by an empty line. The first nonempty line of its contains N (N ≤ 10,000). The next N − 1 lines each contains three integers a, b and c, describing an edge connecting nodes a and b with weight c. The edges are numbered in the order they appear in the input. Below them are the instructions, each sticking to the specification above. A lines with the word “DONE” ends the test case.

Output

For each “QUERY” instruction, output the result on a separate line.

Sample Input

1

3
1 2 1
2 3 2
QUERY 1 2
CHANGE 1 3
QUERY 1 2
DONE

Sample Output

1
3

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <vector>
#define INF 0x3f3f3f3f
#define MAX_N 10010
#define find_max(a,b) a>b?a:b
#define find_min(a,b) a>b?b:a
using namespace std;
int n;
struct edge{
	int next;
	int val;
};
struct num_edge{
	int u,v,p;
};
int num=0;//编号变量
int start;//在线段树中的起始
int size[MAX_N];//用来保存以x为根的子树节点个数
int top[MAX_N];//用来保存当前节点的所在链的顶端节点
int son[MAX_N];//用来保存重儿子
int depth[MAX_N];//用来保存当前节点的重链的深度
int fa[MAX_N];//用来保存当前节点的父亲
int tid[MAX_N];//用来保存树中每个节点剖分后的新编号
int rank[MAX_N];//用来保存线段树中各位置对应的节点
int dat[4*MAX_N];//区间最大值线段树数组
int val[MAX_N];//用来保存该点到父亲的边权值
vector<edge> g[MAX_N];//存储节点的边
vector<num_edge> list;//按输入顺序存储边
void dat_change(int,int);
int get_count()
{//对树节点的个数取对数，小数点进位
	int count=0;
	int t=n;
	while(t)
	{
		t/=2;
		++count;
	}
	return count;
}
void init()
{//初始化
	num=0;//标号置0
	list.clear();//清空编号
	for(int i=0;i<=n;++i)
	{//清空边
		g[i].clear();
		son[i]=-1;
	}
	start=(1<<get_count())-1;//线段树用
	for(int i=0;i<=start*2+1;++i)//把线段树的数组元素置为负无穷
		dat[i]=-INF;
}
void add_edge(int u,int v,int p)
{//添边
	g[u].push_back((edge){v,p});
	g[v].push_back((edge){u,p});
}
void first_dfs(int u,int father)
{//第一深搜，确定每个节点的：重儿子、父亲、值
	fa[u]=father;
	size[u]=1;
	for(int i=0;i<g[u].size();++i)
	{
		int v=g[u][i].next;
		if(v!=father)
		{
			val[v]=g[u][i].val;
			first_dfs(v,u);
			size[u]+=size[v];
			if(son[u]==-1||size[v]>size[son[u]])//son记录重儿子
				son[u]=v;
		}
	}
}
void second_dfs(int u,int _top)
{//第二次深搜，确定每个节点的：重链顶部、标号、反标号、深度
	top[u]=_top;
	tid[u]=++num;
	dat_change(u,val[u]);
	rank[tid[u]]=u;
	if(son[u]==-1)
		return;
	depth[son[u]]=depth[u];
	second_dfs(son[u],_top);//优先搜索重儿子
	for(int i=0;i<g[u].size();++i)
	{//其后再搜索轻儿子
		int v=g[u][i].next;
		if(v!=son[u]&&v!=fa[u])
		{
			depth[v]=depth[u]+1;
			second_dfs(v,v);
		}
	}
}
int get_lca(int a,int b)
{//寻找从a到b路径的LCA
	int u=depth[a]>=depth[b]?a:b;
	int v=depth[a]>=depth[b]?b:a;
	while(depth[u]>depth[v])//深度齐平
		u=fa[top[u]];
	//上溯至同一重链
	while(top[u]!=top[v])
	{
		u=fa[top[u]];
		v=fa[top[v]];
	}
	//在同一重链中，标号是连续的，且标号小的为祖先，所以标号小的肯定为LCA
	int lca=tid[u]>tid[v]?v:u;
	return lca;
}
void dat_change(int a,int b)
{//线段树上的更新
	int ndat=start+tid[a];
	dat[ndat]=b;
	while(ndat>0)
	{
		ndat/=2;
		dat[ndat]=find_max(dat[ndat*2],dat[ndat*2+1]);
	}
}
void change(int i,int val)
{//修改编号为i的边的值
	int u=list[i-1].u;
	int v=list[i-1].v;
	if(fa[u]==v)
		dat_change(u,val);
	else dat_change(v,val);
	list[i-1].p=val;
}
void negate(int a,int b)
{//对a到b路径上的边的值变反并更新
	int lca=get_lca(a,b);
	while(a!=lca)
	{
		dat_change(a,-1*dat[start+tid[a]]);
		a=fa[a];
	}
	while(b!=lca)
	{
		dat_change(b,-1*dat[start+tid[b]]);
		b=fa[b];
	}
	//change(lca,-1*dat[start+tid[lca]]);
}
int dat_query(int a,int b,int l,int r,int k)
{//线段树上的查询
	// printf("a:%d b:%d l:%d r:%d k:%d\n",a,b,l,r,k);
	//在查询区间外
	if(r<a||b<l)
		return -INF;
	//在查询区间内
	if(a<=l&&r<=b)
		return dat[k];
	else
	{//与查询区间有交集
		int vl=dat_query(a,b,l,(l+r)/2,2*k);
		int vr=dat_query(a,b,(l+r)/2+1,r,2*k+1);
		return find_max(vl,vr);
	}
}
int query(int a,int b)
{
	int res=-INF;
	int lca=get_lca(a,b);
	// printf("lca:%d\n", lca);
	// printf("1\n");
	while(top[a]!=top[lca])
	{
		res=find_max(res,dat_query(tid[top[a]],tid[a],1,start+1,1));
		// printf("tid: %d - %d\n", tid[top[a]],tid[a]);
		// printf("#tree: %d - %d\n", top[a],a);
		a=fa[top[a]];
	}
	// printf("2\n");
	while(top[b]!=top[lca])
	{
		res=find_max(res,dat_query(tid[top[b]],tid[b],1,start+1,1));
		// printf("tid: %d - %d\n", tid[top[b]],tid[b]);
		// printf("#tree: %d - %d\n", top[b],b);
		b=fa[top[b]];
	}
	int u=tid[a]>tid[b]?b:a;
	int v=tid[a]>tid[b]?a:b;
	// printf("3 # u:%d v:%d\n",u,v);
	if(u!=v)
	{
		u=son[u];
		res=find_max(res,dat_query(tid[u],tid[v],1,start+1,1));
		//printf("tid: %d - %d\n", tid[u],tid[v]);
		// printf("#tree: %d - %d\n", u,v);
	}
	return res;
}
void solve()
{
	int root=1;
	//进行树链剖分
	first_dfs(root,-1);
	second_dfs(root,root);
	// printf("start:%d \n",start);
	// for(int i=1;i<=n;++i)
	// {
	// 	printf("size[%d]:%d  ",i,size[i] );
	// 	printf("top[%d]:%d  ",i, top[i]);
	// 	printf("son[%d]:%d  ",i, son[i]);
	// 	printf("fa[%d]:%d  ", i,fa[i]);
	// 	printf("tid[%d]:%d  ", i,tid[i]);
	// 	printf("val[%d]:%d  ", i,val[i]);
	// 	printf("\n");
	// }
	// for(int i=1;i<=2*start+1;++i)
	// 	printf(" i:%d %d \n",i,dat[i]);
	//处理改、查
	char str[10];
	char choice[4][10]={"QUERY","NEGATE","CHANGE","DONE"};
	int a,b;

	scanf("%s",str);
	while(strcmp(str,choice[3]))
	{
		scanf("%d %d",&a,&b);
		if(!strcmp(str,choice[0]))
			printf("%d\n",query(a,b));
		else if(!strcmp(str,choice[1]))
			negate(a,b);
		else if(!strcmp(str,choice[2]))
			change(a,b);

		scanf("%s",str);
	}
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		init();
		int u,v,p;
		for(int i=0;i<n-1;++i)
		{
			scanf("%d %d %d",&u,&v,&p);
			list.push_back((num_edge){u,v,p});
			add_edge(u,v,p);
		}
		solve();
	}
	return 0;
}
/*
100
14
1 2 3
1 3 4
1 4 5
2 5 3
2 6 4
3 7 5
4 8 2
4 9 10
5 10 7
6 11 4
6 12 4
8 13 20
13 14 13

*/

兔衰

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
树链剖分理解&&poj 3237

树链剖分用一句话概括就是：把一棵树剖分为若干条链，然后利用数据结构(树状数组，SBT，Splay，线段树等等)去维护每一条链，复杂度为O(logn)假如一个树就是一条链的话（极限的想想），我们可以用数据结构（线段树，树桩数组）去维护它。下图 1-6就是一个链树，用树状数组维护这个性质很好，维护很方便然后再画个树，咱们强行用树状数组维
复制链接

扫一扫