题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1159
题目大意:给出两个字符串,求两个字符串的最长公共字串。
思路:慢慢重心开始有贪心转向动态规划了,这题就是简单的动态规划题。以题目的第一组测试数据为例。abcfbc abfcab。
辅助空间变化示意图
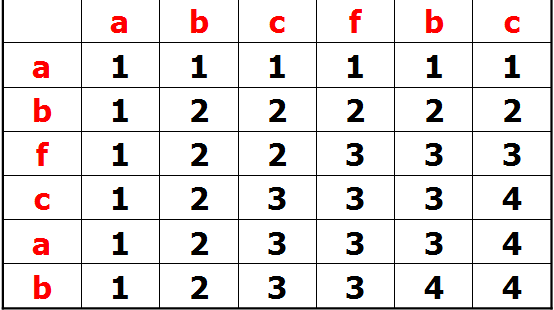
可以看出:
F[i][j]=F[i-1][j-1]+1;(a[i]==b[j])
F[i][j]=max(F[i-1][j],F[i][j-1])(a[i]!=b[j]);
n由于F(i,j)只和F(i-1,j-1), F(i-1,j)和F(i,j-1)有关, 而在计算F(i,j)时, 只要选择一个合适的顺序, 就可以保证这三项都已经计算出来了, 这样就可以计算出F(i,j). 这样一直推到f(len(a),len(b))就得到所要求的解了.
#include<stdio.h>
#include<string.h>
int f[1001][1001];//**1001*1001太大不能定义在主函数,否则直接停止编译**//
int main()
{
char a[1001],b[1001];
int i,j,len1,len2;
while(~scanf("%s %s",a,b))
{
len1=strlen(a);
len2=strlen(b);
for(i=0;i<=len1;i++)
{
f[i][0]=0;
}
for(i=0;i<=len2;i++)
{
f[0][i]=0;
}
for(i=1;i<=len1;i++)
{
for(j=1;j<=len2;j++)
{
if(a[i-1]==b[j-1])
{
f[i][j]=f[i-1][j-1]+1;
}
else
{
f[i][j]=f[i-1][j]>f[i][j-1]?f[i-1][j]:f[i][j-1];
}
}
}
printf("%d\n",f[len1][len2]);
}
return 0;
}







 本文介绍了一个使用动态规划解决字符串匹配问题的方法,具体是求解两个字符串之间的最长公共子串。通过构建状态转移矩阵并进行迭代计算,最终得出最长公共子串的长度。
本文介绍了一个使用动态规划解决字符串匹配问题的方法,具体是求解两个字符串之间的最长公共子串。通过构建状态转移矩阵并进行迭代计算,最终得出最长公共子串的长度。
















 430
430

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








