整数在内存中的存储方式比较简单,我们来看看小数在内存中的存储方式。首先,要学会十进制小数与二进制小数之间的转换。
(1)二进制小数转化为十进制小数
比如把二进制小数110.11转化为十进制小数,步骤如下:
(2)十进制小数转化为二进制小数
方法是这样的:先分别把十进制小数的整数部分和小数部分转化为二进制,然后合并即可。当然整数部分很简单,直接进行二进制转化,而小数部分就不一样了。
具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的整数部分为零,或者整数部分为1,此时0或1为二进制的最后一位,或者达到所要求的精度为止。比如:
将十进制小数173.8125转化为二进制小数
即
所以最终得到:
那么,小数在内存中是怎么存储的呢?
无论是单精度小数还是双精度小数,在存储中都分为三个部分。
(1)符号位 0代表正,1代表负
(2)指数位 用于存储科学计数法中的指数数据,并且采用移位存储
(3)尾数部分
指数有正有负,注意指数位采用移位存储,偏移量为127,假设指数为2,那么指数码表示为129的二进制形式,即10000001
在内存中从高位到低位依次是符号位,指数位和尾数部分。
float 的符号位占1位,指数位占8位,尾数部分占23位
double 的符号位占1位,指数位占11位,尾数部分占52位
我们以173.8125为例,我们知道计算机只认识二进制数据,由于173.8125对应的二进制数据为10101101.1101
那么把10101101.1101写成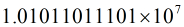
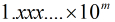
所以173.8125在内存中存储为0 10000110 01011011100000000000000
下面有一段代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
int main()
{
float x = 1.0;
cout<<(int &)x<<endl;
cout<<*(int *)&x<<endl;
return 0;
}
我们发现输出结果均为1065353216
分析:
由于1.0为float型数据,占4字节,可以知道1.0在内存中存储为0
01111111 00000000000000000000000,对于语句 *(int *)&x,意思就是说先将float型的x的指针强制转换为int型的指针,然后取出值。由于是按照float型数据存储的,而却解释成int型,即对应的int整数为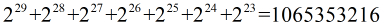





 本文详细介绍了如何将十进制小数转换为二进制小数,并解释了单精度(float)与双精度(double)浮点数在内存中的存储原理。通过实例说明了符号位、指数位及尾数部分的具体含义。
本文详细介绍了如何将十进制小数转换为二进制小数,并解释了单精度(float)与双精度(double)浮点数在内存中的存储原理。通过实例说明了符号位、指数位及尾数部分的具体含义。
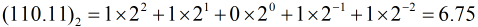
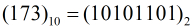
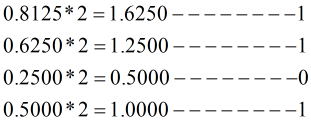
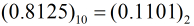
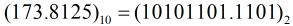
















 2506
2506

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








