一、梯度下降算法
以函数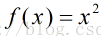
(1)求梯度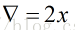
(2)向梯度相反方向移动x, 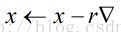
(3)循环迭代步骤(2),直到x的变化到使得f(x)在两次迭代之间的差值足够小,比如0.00000001,即直到两次迭代计算出来的f(x)基本没有变化,则说明此时f(x)已经达到局部最小值了;
(4)输出x,这个x就是使函数f(x)最小时x的取值
注意:梯度的方向就是导数最大值的方向,即函数变化率最快的方向。因此,梯度方向可以通过对函数求导得到。
梯度下降算法计算过程
(1)初始化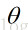
(2)迭代,新的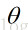
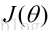
(3)如果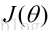
例如,线性回归目标函数的梯度方向计算
梯度下降算法又分为,批量梯度下降算法和随机梯度下降算法。
1.批量梯度下降算法
批量梯度下降法一般而言只能找到局部最小的值,但对于凸函数,则一定能找到全局最优的值。另外,线性函数都是凸函数,因为
根据m个样本的梯度和调整下降
2.随机梯度下降算法
每一个样本算一次,不是批量梯度下降。
批量梯度下降一定能下降到(全局)或局部最小值,但是随机梯度下降会发生跳动,不够稳定下降,但是在不能全部获取样本时,随机梯度下降算法会比较合适。对于存在平坦部分的曲线,采用批量梯度下降算法时,下降到平坦处会下降不了,但随机梯度下降由于跳跃性,还可以往下下降。
3.学习率的确定
对于固定学习率下,梯度下降的运行过程:
(1) 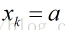
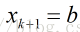
(2)从x0为出发点,每次沿着当前函数梯度反方向移动一定距离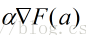
(3)对应的各点函数值序列之间的关系为:
(4)当n达到一定值时,函数f(x)收敛到局部最小值
很多时候,我们没有先验知识,则无法确定学习率,此时需要采用一种方法求出学习率。
视角转换
记当前点为xk点,当前搜索方向为dk(如:负梯度方向),因为学习率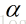
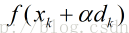
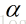
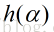
因为梯度下降法是寻找f(x)的最小值,那么,在xk和dk给定的前提下,即寻找函数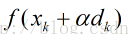
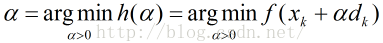
如果h(a)可导,局部最小值处的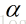
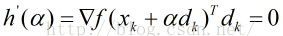
为什么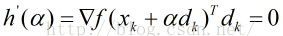
学习率确定的三种方式:
1.线性搜索
为最简单的处理方式为二分线性搜索,不断将区间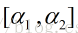
2.回溯线性搜索
基于Armijo准则计算搜索方向上的最大步长,其基本思想是沿着搜索方向移动一个较大的步长估计值,然后以迭代形式不断减小步长,直到该步长使得函数值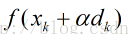
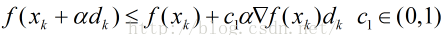
两种搜索方法的异同:
(1)二分线性搜索的目标是求得满足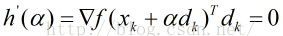
(2)二分线性搜索可以减少下降次数,但在计算最优步长上花费了不少代价,回溯线性搜索找到一个差不多的步长即可。
3.二次插值线性搜索法
采用多项式插值法拟合简单函数,然后根据该简单函数估计函数的极值点,这样选择合适步长的效率会高很多。
现在拥有的数据为:xk处的函数值f(xk)及其导数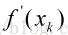
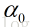
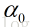
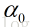
此时,导数为零的最优值为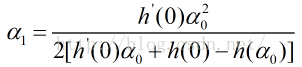
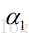
二、牛顿下降法
函数二阶导数反应了函数的凸凹性,二阶导越大,一阶导的变化越大。因此,在搜索中可以用二阶导来做一些修正,比如二者相除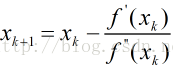
上述迭代公式即为牛顿法,该方法可以直接推广到多维:用方向导数代替一阶导,用Hessian矩阵代替二阶导
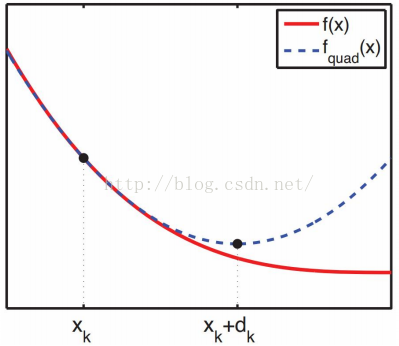
牛顿法本质上是知道某点处
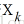
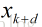
牛顿法的特征
(1)经典牛顿法虽然具有二次收敛性,但是要求初始点需要尽量靠近极小点,否则有可能不收敛;
(2)计算过程中需要计算目标函数的二阶偏导数,难度较大;
(3)目标函数法的Hessian矩阵无法保持正定(即顺序主子式不全大于零),会导致算法产生的方向不能保证是f在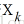
(4)如果Hessian矩阵奇异,牛顿方向可能根本是不存在的。即|H|=0,二阶偏导数此时为Hessian矩阵为分母,如果行列式为0,则无意义。
牛顿法应用了泰勒展开式,是属于二阶导、二阶收敛,而梯度下降是一阶收敛,二阶其实相当于考虑了梯度的梯度,因此牛顿法下降法相对更快。








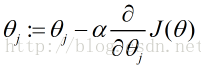
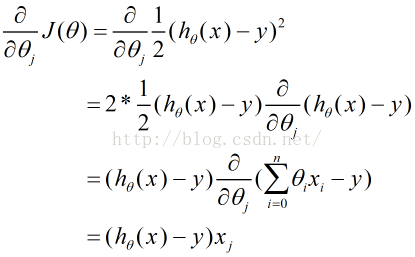
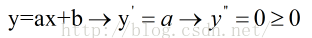
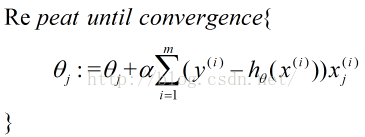
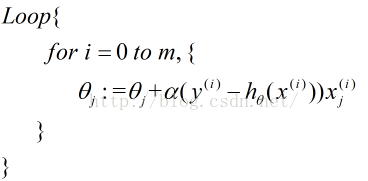
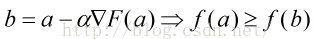
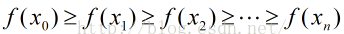
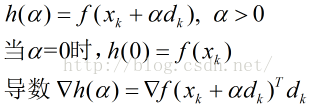
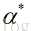
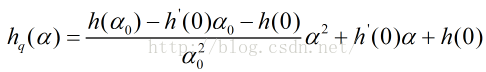
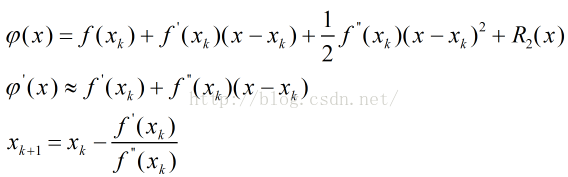













 797
797











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








