机器学习（十五）——loss function比较、独立成分分析

http://antkillerfarm.github.io/

PCA算法推导（续）

对u求导可得：

$$\nabla_u\mathcal{L}(u)=\Sigma u-\lambda u$$

这里的矩阵求导步骤，参见《机器学习（九）》中的公式5.12的推导过程。

令导数为0可得，当$\lambda$为$\Sigma$的特征值的时候，该代价函数得到最优解。

注：这里的推导过程，求解的是1维的PCA，但结论对于k维的PCA也是成立的。

一个n阶矩阵有n个特征值，这些特征值可按绝对值大小排序，绝对值越大的，越重要。其中最大的k个特征值，被称作k principal components，这就是主成分分析（Principal components analysis，PCA）算法的命名来历。

我们以最大的k个特征值所对应的特征向量，构建样本空间Y：

$$y^{(i)}=\begin{bmatrix} u_1^Tx^{(i)}\\ u_2^Tx^{(i)}\\ \cdots \\ u_k^Tx^{(i)} \end{bmatrix}\in R^k\tag{1}$$

可以看出PCA算法实际上是个降维（dimensionality reduction）算法。

PCA的用途

为了便于理解PCA算法，我们以如下图片的处理过程为例，进行说明。

第一排从左往右依次为：原图（450*333）、k=1、k=5；第二排从左往右依次为：k=20、k=50。

从中可以看出，k=50时，图像的效果已经和原图相差无几。而原图是个450*333的高阶矩阵。

在图像处理领域，奇异值不仅可以应用在数据压缩上，还可以对图像去噪。如果一副图像包含噪声，我们有理由相信那些较小的奇异值就是由于噪声引起的。当我们强行令这些较小的奇异值为0时，就可以去除图片中的噪声。

PCA的一个很大的优点是，它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。

但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。

PCA和ALS的联系与区别

令：

$$Y_{k\times m}=\begin{bmatrix}y^{(1)} & \cdots & y^{(m)}\end{bmatrix}$$

则由公式1可得：

$$Y_{k\times m}=U_{n\times k}^TX_{n\times m}$$

变换可得：

$$X_{n\times m}\approx U_{n\times k}Y_{k\times m}$$

由于PCA是个降维算法，因此这个变换实际上也是个近似变换。

从上面可以看出，PCA和ALS实际上都是矩阵的降维分解算法。它们的差别在于：

1.PCA的U矩阵是单位正交矩阵，而ALS的分解矩阵则没有这个限制。

2.ALS从原理上虽然也是矩阵的奇异值或特征值的应用，然而其求解过程，却并不涉及矩阵的奇异值或特征值的运算，因此运算效率非常高。

3.ALS是个迭代算法，容易掉入局部最优陷阱中。

PCA和特征选择的区别

两者虽然都是降维算法，但特征选择是在原有的n个特征中选择k个特征，而PCA是重建k个新的特征。

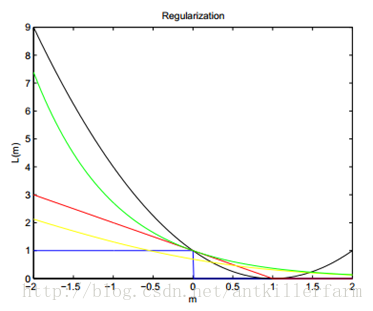
loss function比较

这里m代表了置信度，越靠近右边置信度越高。

其中蓝色的阶跃函数又被称为Gold Standard，黄金标准，因为这是最准确无误的分类器loss function了。分对了loss为0，分错了loss为1，且loss不随到分界面的距离的增加而增加，也就是说这个分类器非常鲁棒。但可惜的是，它不连续，求解这个问题是NP-hard的，所以才有了各种我们熟知的分类器。

其中红色线条就是SVM了，由于它在m=1处有个不可导的转折点，右边都是0，所以分类正确的置信度超过一定的数之后，对分界面的确定就没有一点贡献了。

黄色线条是Logistic Regression的损失函数，与SVM不同的是，它非常平滑，但本质跟SVM差别不大。

绿色线条是boost算法使用的损失函数。

黑色线条是ELM（Extreme learning machine）算法的损失函数。它的优点是有解析解，不必使用梯度下降等迭代方法，可直接计算得到最优解。但缺点是随着分类的置信度的增加，loss不降反升，因此，最终准确率有限。此外，解析算法相比迭代算法，对于大数据的适应较差，这也是该方法的局限所在。

参见：

https://www.zhihu.com/question/28810567

独立成分分析

这一节我们将讲述独立成分分析（Independent Components Analysis，ICA）算法。

首先，我们介绍一下经典的鸡尾酒宴会问题(cocktail party problem)。

假设在party中有n个人，他们可以同时说话，我们也在房间中放置了n个声音接收器(Microphone)用来记录声音。宴会过后，我们从n个麦克风中得到了m组数据$x^{(i)}$，其中的i表示采样的时间顺序。由于宴会上人们的说话声是混杂在一起的，因此，采样得到的声音也是混杂不清的，那么我们是否有办法从混杂的数据中，提取出每个人的声音呢？

为了更为正式的描述这个问题，我们假设数据$s\in R^n$是由n个独立的源生成的。我们接收到的信号可写作：$x=As$。其中，A被称为混合矩阵（mixing matrix）。在这个问题中，$s^{(i)}$是一个n维向量，$s_j^{(i)}$表示第j个说话者在i时刻的声音。同理，$x_j^{(i)}$表示第j个麦克风在i时刻的记录下的数据。

我们把$W=A^{-1}$称作unmixing matrix。我们的目标就是找到W，然后利用$s=Wx$，求得s。我们使用$w_i^T$表示W矩阵的第i行，因此：$s_j^{(i)}=w_j^Tx^{(i)}$。

ICA的不确定性

不幸的是，在没有源和混合矩阵的先验知识的情况下，仅凭$x^{(i)}$是没有办法求出W的。为了说明这一点，我们引入置换矩阵的概念。

置换矩阵（permutation matrix）是一种元素只由0和1组成的方块矩阵。置换矩阵的每一行和每一列都恰好只有一个1，其余的系数都是0。它的例子如下：

$$P=\begin{bmatrix}0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}; P=\begin{bmatrix}0 & 1 \\ 1 & 0 \end{bmatrix}; P=\begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix}$$

在线性代数中，每个n阶的置换矩阵都代表了一个对n个元素（n维空间的基）的置换。当一个矩阵乘上一个置换矩阵时，所得到的是原来矩阵的横行（置换矩阵在左）或纵列（置换矩阵在右）经过置换后得到的矩阵。

ICA的不确定性(ICA ambiguities)包括以下几种情形：

1.无法区分W和WP。比如改变说话人的编号，会改变$s^{(i)}$的值，但却不会改变$x^{(i)}$的值，因此也就无法确定$s^{(i)}$的值了。

2.无法确定W的尺度。比如$x^{(i)}$还可以写作$x^{(i)}=2A \cdot (0.5)s^{(i)}$，因此在不知道A的情况下，同样无法确定$s^{(i)}$的值。

3.信号不能是高斯分布的。

假设两个人发出的声音信号符合多值正态分布$s\sim \mathcal{N}(0,I)$，这里的I是一个2阶单位阵，则$E[xx^T]=E[Ass^TA^T]=AA^T$。

假设R是正交矩阵，$A'=AR,x'=A's$，则：

$$E[xx^T]=E[A'ss^T(A')^T]=E[ARss^T(AR)^T]=ARR^TA^T=AA^T$$

可见，无论是A还是A’，观测值x都是一个$\mathcal{N}(0,AA^T)$的正态分布，也就是说A的值无法确定，那么W和s也就无法求出了。

密度函数和线性变换

在讨论ICA的具体算法之前，我们先来回顾一下概率和线性代数里的知识。

假设我们的随机变量s有概率密度（probability density）函数$p_s(s)$。为了简单，我们再假设s是实数，还有一个随机变量$x=As$，A和x都是实数。令$p_x$是x的概率密度，那么怎么求$p_x$呢？

令$W=A^{-1}$，则$s=Wx$。然而$p_x(x)\neq p_s(Wx)$。

这里以均匀分布（Uniform）为例讨论一下。令$s\sim \text{Uniform}[0,1]$，则$p_s(s)=1$。令$A=2$，则$W=0.5$，$x=2s\sim \text{Uniform}[0,2]$，因此$p_x(x)=p_s(Wx)\lvert W \rvert$。

累积分布函数

累积分布函数（cumulative distribution function，CDF）是概率论中的一个基本概念。它的定义如下：

$$F(z_0)=P(z\le z_0)=\int_{-\infty}^{z_0}p_z(z)\mathrm{d}z$$

可以看出：

$$p_z(z)=F'(z)$$

ICA算法

ICA算法归功于Bell 和 Sejnowski，这里使用最大似然估计来解释算法。（原始论文中使用的是一个复杂的方法Infomax principal，这在最新的推导中已经不需要了。）

注：Terrence (Terry) Joseph Sejnowski，1947年生，美国科学家。普林斯顿大学博士，导师是神经网络界的大神John Hopfield。ICA算法和Boltzmann machine的发现人。

Tony Bell的个人主页：
http://cnl.salk.edu/~tony/index.html

我们假定每个$s_i$有概率密度$p_s$，那么给定时刻原信号的联合分布就是：

$$p(s)=\prod_{i=1}^np_s(s_i)$$

因此：

$$p(x)=\prod_{i=1}^np_s(w_i^Tx)\cdot |W|\tag{2}$$

为了确定$s_i$的概率密度，我们首先要确定它的累计分布函数$F(x)$。而这需要满足两个性质：单调递增和在$[0,1]$区间。

我们发现sigmoid函数很适合，它的定义域负无穷到正无穷，值域0到1，缓慢递增。因此，可以假定s的累积分布函数符合sigmoid函数：

$$g(s)=\frac{1}{1+e^{-s}}$$

求导，可得：

$$p_s(s)=g'(s)=g(s)(1-g(s))$$

这里的推导参见《机器学习（一）》的公式7。

注：如果有其他先验信息的话，这里的$g(s)$也可以使用其他函数。否则的话，sigmoid函数能够在大多数问题上取得不错的效果。

公式2的对数似然估计函数为：

$$\ell(W)=\sum_{i=1}^m\left(\sum_{j=1}^m\log g'(w_j^Tx^{(i)})+\log|W|\right)\tag{3}$$

因为：

$$\begin{align} (\log g'(s))'&=(\log [g(s)(1-g(s))])'=(\log g(s))'+(\log (1-g(s)))' \\&=\frac{g'(s)}{g(s)}+\frac{(1-g(s))'}{(1-g(s))}=\frac{g(s)(1-g(s))}{g(s)}-\frac{g(s)(1-g(s))}{(1-g(s))} \\&=1-2g(s) \end{align}$$

又因为《机器学习（九）》的公式5.11，可得公式3的导数为：

$$\nabla_W\ell(W)=\begin{bmatrix} 1-2g(w_1^Tx^{(i)}) \\ 1-2g(w_2^Tx^{(i)}) \\ \vdots \\ 1-2g(w_n^Tx^{(i)}) \end{bmatrix}x^{(i)^T}+(W^T)^{-1}$$

最后，用通常的随机梯度上升算法，求得$\ell(W)$的最大值即可。

注意：我们计算最大似然估计时,假设了$x^{(i)}$和$x^{(j)}$之间是独立的，然而对于语音信号或者其他具有时间连续依赖特性(比如温度)上，这个假设不能成立。但是在数据足够多时，假设独立对效果影响不大。