/*
Copyright (c)2016,烟台大学计算机与控制工程学院
All rights reserved.
文件名称:排序.cpp
作 者: 周国亮
完成日期:2016年12月8日
版 本 号:v1.0
问题描述:设计一个函数,产生一个至少5万条记录的数据集合。在同一数据集上,用直接
插入排序、冒泡排序、快速排序、直接选择排序、堆排序、归并排序、基数排序
等算法进行排序,记录所需要的时间,经过对比,得到对复杂度不同的各种算法
在运行时间方面的感性认识。
提示1:这一项目需要整合多种排序算法,可以考虑先建设排序算法库,作为我们
这门课算法库的收官之作;
提示2:本项目旨在获得对于复杂度不同算法的感性认识,由于数据分布特点、计算
机运行状态等不同,其结果并不能完全代替对算法复杂度的理论分析;
提示3:由于C语言标准提供的时间函数只精确到秒,几种O(nlog2n)级别的算法,在
5万条记录的压力下,并不能明显地看出优劣,可以忽略直接插入排序、冒泡
排序、直接选择排序这三种相对低效率的算法(以节约时间。若能够忍受他们
长时间地运行,请自便),成10倍地加大数据量,然后进行观察。
输入描述:无
程序输出:若干1.测试用的主控程序——main.cpp
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
#include <time.h>
#include "sort.h"
void GetLargeData(RecType *&R, int n)
{
srand(time(0));
R=(RecType*)malloc(sizeof(RecType)*n);
for(int i=0; i<n; i++)
R[i].key= rand(); //产生0~RAND_MAX间的数
printf("生成了%d条记录\n", n);
}
//调用某一排序算法完成排序,返回排序用时
long Sort(RecType *&R, int n, void f(RecType*, int))
{
int i;
long beginTime, endTime;
RecType *R1=(RecType*)malloc(sizeof(RecType)*n);
for (i=0;i<n;i++)
R1[i]=R[i];
beginTime = time(0);
f(R1,n);
endTime = time(0);
free(R1);
return endTime-beginTime;
}
//调用基数排序算法完成排序,返回排序用时
long Sort1(RecType *&R, int n)
{
long beginTime, endTime;
RadixRecType *p;
CreateLink(p,R,n);
beginTime = time(0);
RadixSort(p);
endTime = time(0);
DestoryLink(p);
return endTime-beginTime;
}
int main()
{
RecType *R;
int n = MaxSize; //测试中, MaxSize取50W
GetLargeData(R, n);
printf("各种排序花费时间:\n");
printf(" 直接插入排序:%ld\n", Sort(R, n, InsertSort));
printf(" 希尔排序:%ld\n", Sort(R, n, ShellSort));
printf(" 冒泡排序:%ld\n", Sort(R, n, BubbleSort));
printf(" 快速排序:%ld\n", Sort(R, n, QuickSort));
printf(" 直接选择排序:%ld\n", Sort(R, n, SelectSort));
printf(" 堆排序:%ld\n", Sort(R, n, HeapSort));
printf(" 归并排序:%ld\n", Sort(R, n, MergeSort));
printf(" 基数排序:%ld\n", Sort1(R, n));
free(R);
return 0;
}2.头文件 —— sort.h
#ifndef SORT_H_INCLUDED
#define SORT_H_INCLUDED
#define MaxSize 50000 //最多的数据,取5万,只测试快速算法,可以往大调整
//下面的符号常量和结构体针对基数排序
#define Radix 10 //基数的取值
#define Digits 10 //关键字位数
typedef int KeyType; //定义关键字类型
typedef char InfoType[10];
typedef struct //记录类型
{
KeyType key; //关键字项
InfoType data; //其他数据项,类型为InfoType
} RecType; //排序的记录类型定义
typedef struct node
{
KeyType data; //记录的关键字,同算法讲解中有差别
struct node *next;
} RadixRecType;
void InsertSort(RecType R[],int n); //直接插入排序
void ShellSort(RecType R[],int n); //希尔排序算法
void BubbleSort(RecType R[],int n); //冒泡排序
void QuickSort(RecType R[],int n); //快速排序
void SelectSort(RecType R[],int n); //直接选择排序
void HeapSort(RecType R[],int n); //堆排序
void MergeSort(RecType R[],int n); //归并排序
//下面函数支持基数排序
void CreateLink(RadixRecType *&p,RecType R[],int n); //创建基数排序用的链表
void DestoryLink(RadixRecType *&p); //释放基数排序用的链表
void RadixSort(RadixRecType *&p); //基数排序
#endif // SORT_H_INCLUDED3.算法的实现—— sort.cpp
#include "sort.h"
#include <malloc.h>
//1. 对R[0..n-1]按递增有序进行直接插入排序
void InsertSort(RecType R[],int n)
{
int i,j;
RecType tmp;
for (i=1; i<n; i++)
{
tmp=R[i];
j=i-1; //从右向左在有序区R[0..i-1]中找R[i]的插入位置
while (j>=0 && tmp.key<R[j].key)
{
R[j+1]=R[j]; //将关键字大于R[i].key的记录后移
j--;
}
R[j+1]=tmp; //在j+1处插入R[i]
}
}
//2. 希尔排序算法
void ShellSort(RecType R[],int n)
{
int i,j,gap;
RecType tmp;
gap=n/2; //增量置初值
while (gap>0)
{
for (i=gap; i<n; i++) //对所有相隔gap位置的所有元素组进行排序
{
tmp=R[i];
j=i-gap;
while (j>=0 && tmp.key<R[j].key)//对相隔gap位置的元素组进行排序
{
R[j+gap]=R[j];
j=j-gap;
}
R[j+gap]=tmp;
j=j-gap;
}
gap=gap/2; //减小增量
}
}
//3. 冒泡排序
void BubbleSort(RecType R[],int n)
{
int i,j,exchange;
RecType tmp;
for (i=0; i<n-1; i++)
{
exchange=0;
for (j=n-1; j>i; j--) //比较,找出最小关键字的记录
if (R[j].key<R[j-1].key)
{
tmp=R[j]; //R[j]与R[j-1]进行交换,将最小关键字记录前移
R[j]=R[j-1];
R[j-1]=tmp;
exchange=1;
}
if (exchange==0) //没有交换,即结束算法
return;
}
}
//4. 对R[s]至R[t]的元素进行快速排序
void QuickSortR(RecType R[],int s,int t)
{
int i=s,j=t;
RecType tmp;
if (s<t) //区间内至少存在两个元素的情况
{
tmp=R[s]; //用区间的第1个记录作为基准
while (i!=j) //从区间两端交替向中间扫描,直至i=j为止
{
while (j>i && R[j].key>=tmp.key)
j--; //从右向左扫描,找第1个小于tmp.key的R[j]
R[i]=R[j]; //找到这样的R[j],R[i]"R[j]交换
while (i<j && R[i].key<=tmp.key)
i++; //从左向右扫描,找第1个大于tmp.key的记录R[i]
R[j]=R[i]; //找到这样的R[i],R[i]"R[j]交换
}
R[i]=tmp;
QuickSortR(R,s,i-1); //对左区间递归排序
QuickSortR(R,i+1,t); //对右区间递归排序
}
}
//4. 快速排序辅助函数,对外同其他算法统一接口,内部调用递归的快速排序
void QuickSort(RecType R[],int n)
{
QuickSortR(R, 0, n-1);
}
//5. 直接选择排序
void SelectSort(RecType R[],int n)
{
int i,j,k;
RecType temp;
for (i=0; i<n-1; i++) //做第i趟排序
{
k=i;
for (j=i+1; j<n; j++) //在当前无序区R[i..n-1]中选key最小的R[k]
if (R[j].key<R[k].key)
k=j; //k记下目前找到的最小关键字所在的位置
if (k!=i) //交换R[i]和R[k]
{
temp=R[i];
R[i]=R[k];
R[k]=temp;
}
}
}
//6. 堆排序辅助之——调整堆
void sift(RecType R[],int low,int high)
{
int i=low,j=2*i; //R[j]是R[i]的左孩子
RecType temp=R[i];
while (j<=high)
{
if (j<high && R[j].key<R[j+1].key) //若右孩子较大,把j指向右孩子
j++; //变为2i+1
if (temp.key<R[j].key)
{
R[i]=R[j]; //将R[j]调整到双亲结点位置上
i=j; //修改i和j值,以便继续向下筛选
j=2*i;
}
else break; //筛选结束
}
R[i]=temp; //被筛选结点的值放入最终位置
}
//6. 堆排序
void HeapSort(RecType R[],int n)
{
int i;
RecType temp;
for (i=n/2; i>=1; i--) //循环建立初始堆
sift(R,i,n);
for (i=n; i>=2; i--) //进行n-1次循环,完成推排序
{
temp=R[1]; //将第一个元素同当前区间内R[1]对换
R[1]=R[i];
R[i]=temp;
sift(R,1,i-1); //筛选R[1]结点,得到i-1个结点的堆
}
}
//7.归并排序辅助1——合并有序表
void Merge(RecType R[],int low,int mid,int high)
{
RecType *R1;
int i=low,j=mid+1,k=0; //k是R1的下标,i、j分别为第1、2段的下标
R1=(RecType *)malloc((high-low+1)*sizeof(RecType)); //动态分配空间
while (i<=mid && j<=high) //在第1段和第2段均未扫描完时循环
if (R[i].key<=R[j].key) //将第1段中的记录放入R1中
{
R1[k]=R[i];
i++;
k++;
}
else //将第2段中的记录放入R1中
{
R1[k]=R[j];
j++;
k++;
}
while (i<=mid) //将第1段余下部分复制到R1
{
R1[k]=R[i];
i++;
k++;
}
while (j<=high) //将第2段余下部分复制到R1
{
R1[k]=R[j];
j++;
k++;
}
for (k=0,i=low; i<=high; k++,i++) //将R1复制回R中
R[i]=R1[k];
}
//7. 归并排序辅助2——一趟归并
void MergePass(RecType R[],int length,int n) //对整个数序进行一趟归并
{
int i;
for (i=0; i+2*length-1<n; i=i+2*length) //归并length长的两相邻子表
Merge(R,i,i+length-1,i+2*length-1);
if (i+length-1<n) //余下两个子表,后者长度小于length
Merge(R,i,i+length-1,n-1); //归并这两个子表
}
//7. 归并排序
void MergeSort(RecType R[],int n) //自底向上的二路归并算法
{
int length;
for (length=1; length<n; length=2*length) //进行log2n趟归并
MergePass(R,length,n);
}
//以下基数排序,为了统一测试有改造
//8. 基数排序的辅助函数,创建基数排序用的链表
void CreateLink(RadixRecType *&p,RecType R[],int n) //采用后插法产生链表
{
int i;
RadixRecType *s,*t;
for (i=0; i<n; i++)
{
s=(RadixRecType *)malloc(sizeof(RadixRecType));
s->data = R[i].key;
if (i==0)
{
p=s;
t=s;
}
else
{
t->next=s;
t=s;
}
}
t->next=NULL;
}
//8. 基数排序的辅助函数,释放基数排序用的链表
void DestoryLink(RadixRecType *&p)
{
RadixRecType *q;
while(p!=NULL)
{
q=p->next;
free(p);
p=q;
}
return;
}
//8. 实现基数排序:*p为待排序序列链表指针,基数R和关键字位数D已经作为符号常量定义好
void RadixSort(RadixRecType *&p)
{
RadixRecType *head[Radix],*tail[Radix],*t; //定义各链队的首尾指针
int i,j,k;
unsigned int d1, d2=1; //用于分离出第i位数字,见下面的注释
for (i=1; i<=Digits; i++) //从低位到高位循环
{
//分离出倒数第i位数字,先通过对d1=10^i取余,得到其后i位,再通过整除d2=10^(i-1)得到第i位
//例如,分离出倒数第1位,即个位数,先对d1=10取余,再整除d2=1
//再例如,分离出倒数第2位,即十位数,先对d1=100取余,再整除d2=10
//循环之前,d2已经初始化为1,在这一层循环末增加10倍
//下面根据d2,得到d1的值
d1=d2*10;
for (j=0; j<Radix; j++) //初始化各链队首、尾指针
head[j]=tail[j]=NULL;
while (p!=NULL) //对于原链表中每个结点循环
{
k=(p->data%d1)/d2; //分离出第i位数字k
if (head[k]==NULL) //进行分配
{
head[k]=p;
tail[k]=p;
}
else
{
tail[k]->next=p;
tail[k]=p;
}
p=p->next; //取下一个待排序的元素
}
p=NULL; //重新用p来收集所有结点
for (j=0; j<Radix; j++) //对于每一个链队循环
if (head[j]!=NULL) //进行收集
{
if (p==NULL)
{
p=head[j];
t=tail[j];
}
else
{
t->next=head[j];
t=tail[j];
}
}
t->next=NULL; //最后一个结点的next域置NULL
//下面更新用于分离出第i位数字的d2
d2*=10;
}
} 取五万条数据时
取五十万条数据时
取三百万条数据时
取四百万条数据时








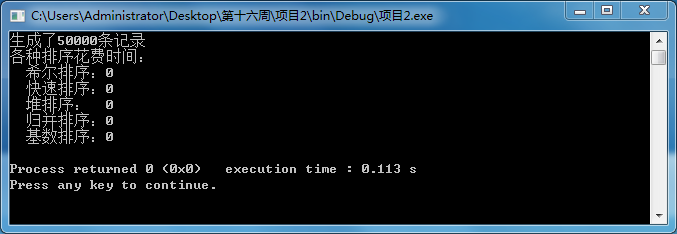
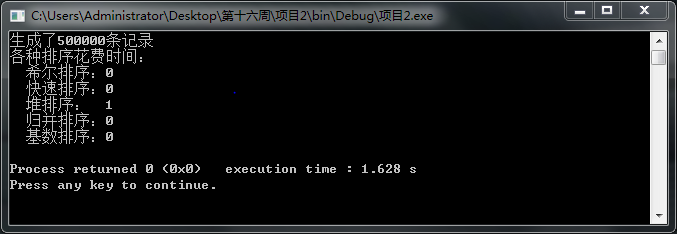


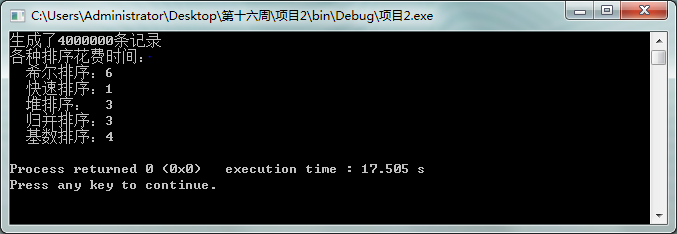














 599
599

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








