哈夫曼树是带权路径最小的一种特殊二叉树,所以也称最优二叉树。
在这里不讨论基本概念如如何计算路径等,而只着重于树的创建,具体过程让我们举例而言。
其基本的原理为:将所有节点一开始都视为森林,每次从森林中选取两个根节点权值最小的树合并为一棵新树,新树的根节点大小为两个子节点大小的和,并将这棵新树重新加入到森林中。
如此一来每一轮操作都可以简化为两个基本操作:合并两棵树、插入新树,直到森林中只剩下一棵树,即是哈夫曼树。
以7个节点的权值分别为 1 3 7 9 12 18 25而言
创建的第一步:合并1、3,新增4
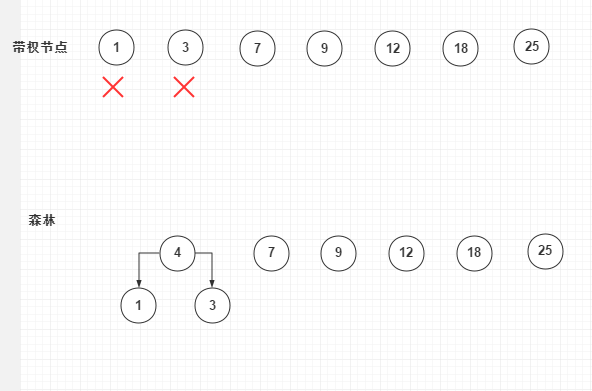
创建的第二步:合并4、7,新增11
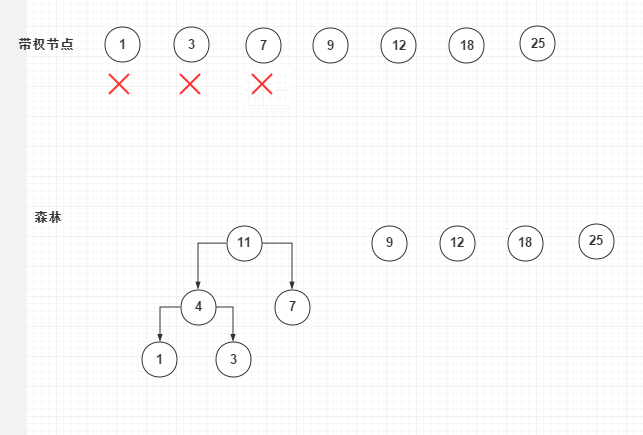
创建的第三步:合并9、11,新增20
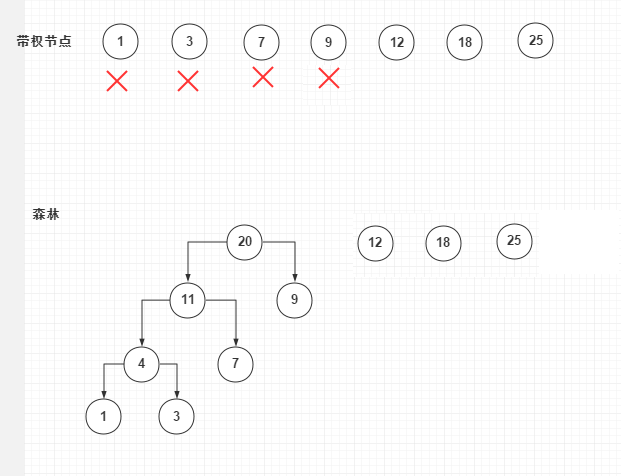
创建的第四步:合并12、18,新增30
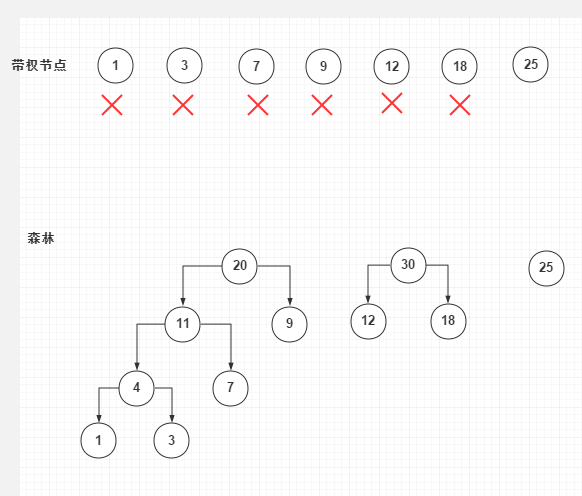
创建的第五步:合并20、25,新增45
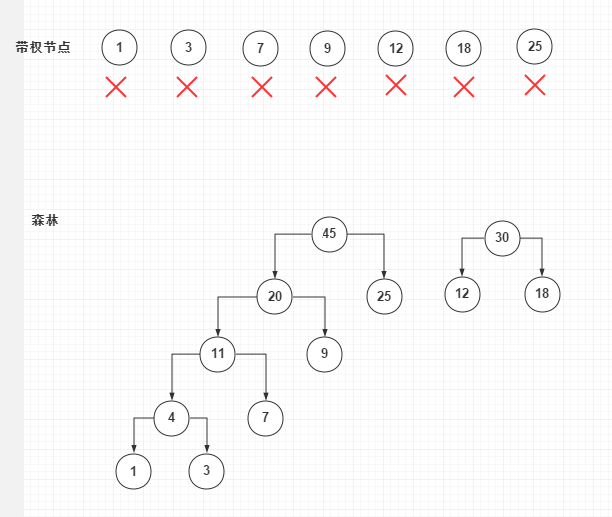
合并最后两棵树,得到哈夫曼树
在程序中我们实际运行来创建这棵树后,进行先序遍历的结果如下:
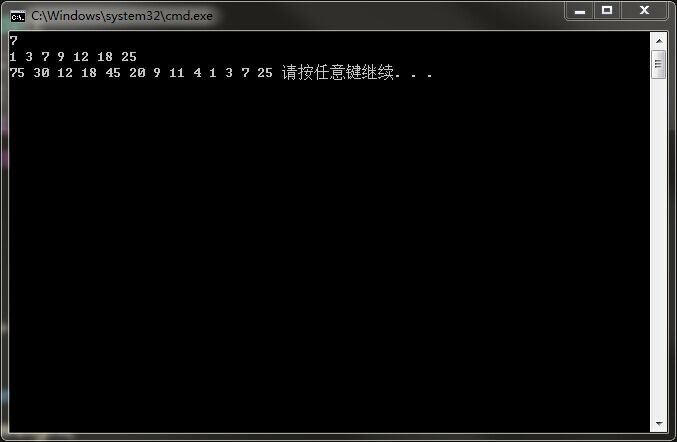
可以看到所有操作是符合结果的
在创建的过程中,很重要的一个过程是:每次都必须从森林中选出节点权值最小的两棵树进行合并,然后插入森林中,这个过程我们可以用最大最小堆的插入和删除来实现,关于最大最小堆的实现和讲解可以看我的这篇客:
http://blog.csdn.net/ava1anche/article/details/46965675
以下是具体的代码和注释,部分操作不做解释,看注释就行了
/*
时间:2015.7.20
名称:哈夫曼树
操作:哈夫曼树的创建、哈夫曼树的层序遍历(方便查看)、哈夫曼树的森林的相关操作(最大最小堆的操作)、树的中序遍历
简述:通过一个哈夫曼树的森林来创建哈夫曼树、每次建立树都从森林中删除两棵树、然后加入一棵新树、
为了使加入和删除更有效率,森林由最大最小堆实现。
*/
#include<iostream>
using namespace std;
int cost = 0;
const int MAX_CAPACITY = 100000;//森林的最大容纳量
enum type{Maxiumn,Miniumn};//代表森林的类型是从大到小还是从小到大
typedef struct Node//树的节点的结构
{
int 







 本文介绍了哈夫曼树(最优二叉树)的创建过程,通过不断合并权值最小的节点来构建。详细步骤包括从森林中选择最小权值节点合并,最终形成单一的哈夫曼树。在实现过程中,利用最大最小堆辅助操作。同时提供了程序代码和先序遍历结果。
本文介绍了哈夫曼树(最优二叉树)的创建过程,通过不断合并权值最小的节点来构建。详细步骤包括从森林中选择最小权值节点合并,最终形成单一的哈夫曼树。在实现过程中,利用最大最小堆辅助操作。同时提供了程序代码和先序遍历结果。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 5310
5310

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








