书接上文(http://blog.csdn.net/baimafujinji/article/details/6472660),我们继续讨论矩阵极限与马尔科夫链的话题。为了证明Thm 5.20,我们还要继续做一些准备工作。
五、证明定理5.20的一些准备(续)
这个定理主要阐释两方面的内容:1)λ>0; 2)u is an 特征向量 of A corresponding to λ and gm(λ) = 1。(gm:几何重数)
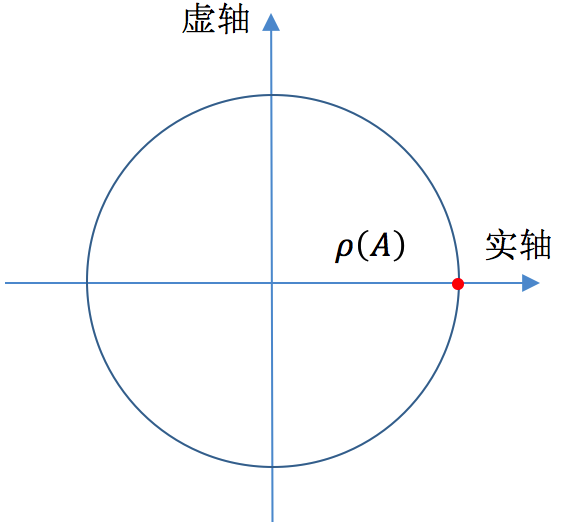
而且这个定理其实给我们一个非强的结论。如下图所示,positive矩阵A的特征值之绝对值 |λ|=“对应的行和”,那么λ仅可能是图中红色的一点,而不可能是以ρ(A)为半径的圆上的其他点。
为了讨论Thm 5.20,我们要做的最后一项准备工作就是要知道如下与转移矩阵A的性质有关之结论:
具体我们分两种情况来讨论:
(I)A是转移矩阵
(II)A是转移矩阵,并且A是regular.
可见情况(II)是情况(I)的一个子集,所以(I)所满足的性质(II)也将会自动满足。
(I)的性质总结为如下三条:
- 如果A是转移矩阵,那么Am也是转移矩阵for any m; Ap (矩阵A与向量p相乘)是一个概率向量 for any 概率向量p;
- 如果λ是A的特征值,则|λ|≤1;
- 1一定是A的一个特征向量。
(II)的性质总结为如下两条(除了上面的三条之外):
- 如果λ是A的特征值,则|λ|≤1 and if |λ|=1 then λ=1 and gm(λ=1)=1
- am(λ=1)=1
其中,(II)的第一条性质如果用图形来表述的话,意思就是在复平面上有一个单位圆,那么A的特征值,要么位于圆内,如果特征值位于圆上,那么只可能取得值等于1的点。
六、矩阵的极限
七、定理Thm 5.20的证明
矩阵的极限与马尔科夫链(上、下)的讨论都主要围绕Thm 5.20展开,这也是我们用于解决实际问题的一个最重要的法宝。在第(五)部分里,我们给出了很多重要的结论可以帮助我们更好地理解Thm 5.20。因为这其中涉及到非常多的复杂的细节,我们没有把所有证明过程详细的铺开。如果你有深入研究的需求,可以参考文献【1】以了解更多。
下面我们把Thm 5.20的主要结论重述一遍——假设A是一个转移矩阵,并且是regular的,那么则有有如下结论:
- |λ|<1 or λ=1,in fact λ=1 是A的一个特征值,而且gm(λ=1)=1
- am(λ=1)=1
存在。
- Let L =
, then (a) L仍然是一个转移矩阵;(b)AL = LA = L
- L=(v,v,...,v), v表示一个列向量,where v is the unique 概率向量 satisfying Av=1v。
显然,结论1-3已经蕴含在第(五)部分中了,我们不做证明。下面来试着证明结论4~6。
Pf : (4-a) 我们的目的是要证明L是一个转移矩阵,那么一个比较简单的方法就是借助Thm 5.15。令u是一个列向量,而且每一个元素都是1,那么
刚好符合Thm 5.15的条件,所以可知L仍然是一个转移矩阵。再来证明(4-b) ,则有
于是可知L=AL=LA,所以结论得证。
接下来证明(5):我们要证明L中的每一个列向量都等于v,不妨设 L=(v1, v2, ..., vn),其中vi表示一个列向量。于是根据刚刚证明的AL=L可得A(v1, v2, ..., vn)=(v1, v2, ..., vn),即(Av1, Av2, ..., Avn)=(v1, v2, ..., vn),两个矩阵相等,则对应的列向量应该相等,即Avi=vi,i = 1, 2, ...,n。注意到L是一个转移矩阵,所以每一列的和都等于1,所以vi不等于0,所以vi不会是零向量,那么它一定是特征向量。而Thm 5.20 的第一条就告诉我们,gm(λ=1)=1,也就是说λ=1的特征向量最多只有1个是线性独立的,于是vi=αv,for all v。而vi本身又是概率向量,所以最后就只有一种选择,即vi=v。结论得证。
最后来证明(6):
所以(6)也得到了证明。
八、一个实例
现在我们就用已经得到的定理在MATLAB中实际算一个例子。不妨用《矩阵的极限与马尔科夫链(上)》一文开始时给出的那个例子来演示一下计算。(应该注意到这个引自文献【2】的例子与本文叙述的方式略有差别,依据本文的习惯,实际计算的转移矩阵应该是前面一篇文章中所给例子的描述时采用的矩阵的转置)
首先我们用MATLAB中的eig()函数来帮助我们计算特征值和特征向量。
>> A
A =
0.6500 0.1500 0.1200
0.2800 0.6700 0.3600
0.0700 0.1800 0.5200
>> [V,D]=eig(A)
V =
-0.4701 -0.8092 0.1087
-0.8017 0.3105 -0.7551
-0.3692 0.4987 0.6465
D =
1.0000 0 0
0 0.5185 0
0 0 0.3215可见,1确实是A的一个特征值,它对应的特征向量是[-0.4701,-0.8017,-0.3692]T,为了使其满足概率向量的要求,我们还要对它进行归一化,于是有
>> V(:,1)/sum(V(:,1))
ans =
0.2865
0.4885
0.2250这便得出了与之前相一致的结果。
(全文完)
本文主要根据台湾交通大学开放课程线性代数(莊重 特聘教授主讲)之授课内容整理,并参考以下文献:
【1】S.H. Friedberg, A.J. Insel, L.E Spence, 4th edition, Linear Algebra, Prentice-Hall, 2003
【2】靳志辉,LDA数学八卦,2013








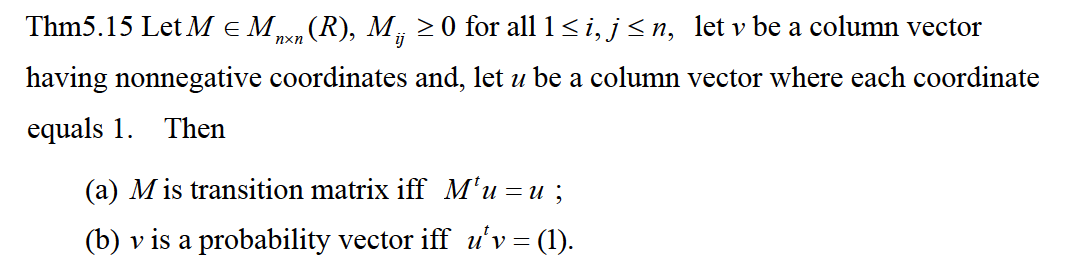

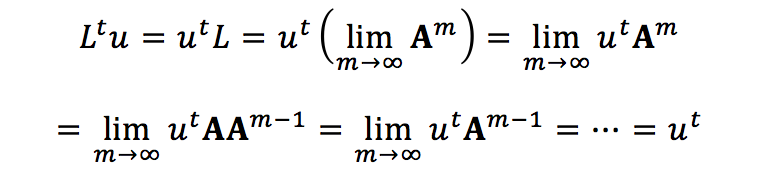
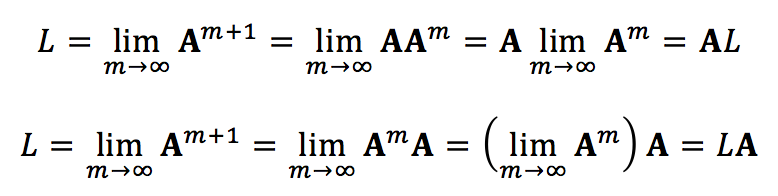
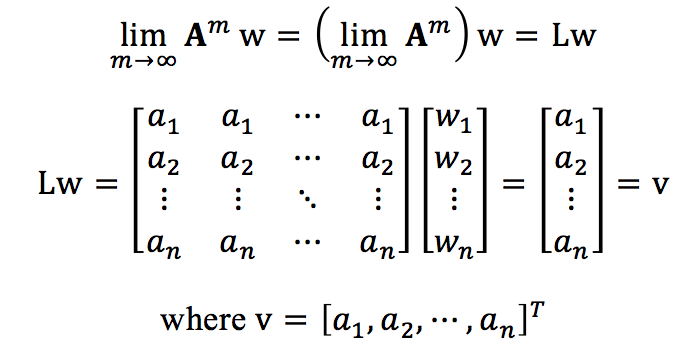


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










