RSA加密算法原理和java简单实现

数学
　　RSA加密算法中，用到素数、互质数、指数运算、模运算等几个数学知识。

素数
　　素数又称质数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数。

互质数
　　百度百科：公因数只有1的两个数，叫做互质数。维基百科：互质，又称互素。若N个整数的最大公因子是1，则称这N个整数互质。

　　常见的互质数判断方法主要有以下几种：

两个不同的质数一定是互质数。例如，2与7、13与19。
一个质数，另一个不为它的倍数，这两个数为互质数。例如，3与10、5与 26。
相邻的两个自然数是互质数。如 15与 16。
相邻的两个奇数是互质数。如 49与 51。
较大数是质数的两个数是互质数。如97与88。
小数是质数，大数不是小数的倍数的两个数是互质数。例如 7和 16。
2和任何奇数是互质数。例如2和87。
1不是质数也不是合数，它和任何一个自然数在一起都是互质数。如1和9908。
辗转相除法。

指数运算
　　指数运算又称乘方计算，计算结果称为幂。nm指将n自乘m次。把nm看作乘方的结果，叫做”n的m次幂”或”n的m次方”。其中，n称为“底数”，m称为“指数”。

模运算
　　模运算即求余运算。“模”是“Mod”的音译。和模运算紧密相关的一个概念是“同余”。数学上，当两个整数除以同一个正整数，若得相同余数，则二整数同余。

　　两个整数a，b，若它们除以正整数m所得的余数相等，则称a，b对于模m同余，记作: a ≡ b (mod m)；读作：a同余于b模m，或者，a与b关于模m同余。例如：26 ≡ 14 (mod 12)。

RSA加密算法

公钥与密钥的产生

　　假设Alice想要通过一个不可靠的媒体接收Bob的一条私人讯息。她可以用以下的方式来产生一个公钥和一个私钥：

随意选择两个大的质数p和q，p不等于q，计算N=pq。
根据欧拉函数，求得r = (p-1)(q-1)
选择一个小于 r 的整数 e，求得 e 关于模 r 的模反元素，命名为d。（模反元素存在，当且仅当e与r互质）
将 p 和 q 的记录销毁。
(N,e)是公钥，(N,d)是私钥。Alice将她的公钥(N,e)传给Bob，而将她的私钥(N,d)藏起来。

加密消息

　　假设Bob想给Alice送一个消息m，他知道Alice产生的N和e。他使用起先与Alice约好的格式将m转换为一个小于N的整数n，比如他可以将每一个字转换为这个字的Unicode码，然后将这些数字连在一起组成一个数字。假如他的信息非常长的话，他可以将这个信息分为几段，然后将每一段转换为n。用下面这个公式他可以将n加密为c：

　　ne ≡ c (mod N)

计算c并不复杂。Bob算出c后就可以将它传递给Alice。

解密消息

Alice得到Bob的消息c后就可以利用她的密钥d来解码。她可以用以下这个公式来将c转换为n：

　　cd ≡ n (mod N)

得到n后，她可以将原来的信息m重新复原。

解码的原理是：

　　cd ≡ n e·d(mod N)

以及ed ≡ 1 (mod p-1)和ed ≡ 1 (mod q-1)。由费马小定理可证明（因为p和q是质数）

　　n e·d ≡ n (mod p) 　　和 　n e·d ≡ n (mod q)

这说明（因为p和q是不同的质数，所以p和q互质）

　　n e·d ≡ n (mod pq)

签名消息

　　RSA也可以用来为一个消息署名。假如甲想给乙传递一个署名的消息的话，那么她可以为她的消息计算一个散列值(Message digest)，然后用她的密钥(private key)加密这个散列值并将这个“署名”加在消息的后面。这个消息只有用她的公钥才能被解密。乙获得这个消息后可以用甲的公钥解密这个散列值，然后将这个数据与他自己为这个消息计算的散列值相比较。假如两者相符的话，那么他就可以知道发信人持有甲的密钥，以及这个消息在传播路径上没有被篡改过。

编程实践

　　在开始编程前，我们通过计算，来确定公钥和密钥。

计算公钥和密钥
假设p = 3、q = 17（p，q都是素数即可。），则N = pq = 51；
r = (p-1)(q-1) = (3-1)(17-1) = 32；
根据模反元素的计算公式，我们可以得出，e·d ≡ 1 (mod 32),即e·d = 32n+1 (n为正整数)；我们假设n=1，则e·d = 33。e、d为正整数，并且e与r互质，则e = 3，d = 11。（两个数交换一下也可以。）
　　到这里，公钥和密钥已经确定。公钥为(N, e) = (51, 3)，密钥为(N, d) = (51, 11)。

编程实现
　　下面我们使用Java来实现一下加密和解密的过程。

public class rsademo {  
      
    /** 
     *  加密、解密算法 
     * @param key 公钥或密钥 
     * @param message 数据 
     * @return 
     */  
    public static long rsa(int baseNum, int key, long message){  
        if(baseNum < 1 || key < 1){  
            return 0L;  
        }  
        //加密或者解密之后的数据  
        long rsaMessage = 0L;  
          
        //加密核心算法  
        rsaMessage = Math.round(Math.pow(message, key)) % baseNum;  
        return rsaMessage;  
    }  
 
    public static void main(String[] args){  
        //基数  
        int baseNum = 3 * 17;  
        //公钥  
        int keyE = 3;  
        //密钥  
        int keyD = 11;  
        //未加密的数据  
        long msg = 28L;  
        //加密后的数据  
        long encodeMsg = rsa(baseNum, keyE, msg);  
        //解密后的数据  
        long decodeMsg = rsa(baseNum, keyD, encodeMsg);  
          
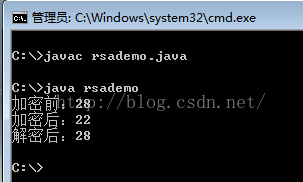
        System.out.println("加密前：" + msg);  
        System.out.println("加密后：" + encodeMsg);  
        System.out.println("解密后：" + decodeMsg);  
          
    }  
}

再计算一次；
p=61,q=53
p*q=3233; 3233写成二进制是110010100001，一共有12位，密钥是12位；
φ(n) = (p-1)(q-1)
φ(3233)=60×52=3120
随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质；
在1到3120之间，随机选择17；
计算e对于φ(n)的模反元素d；
已知 e=17, φ(n)=3120，
　　17x + 3120y = 1
这个方程可以用"扩展欧几里得算法"求解；算出一组整数解为 (x,y)=(2753,-15)，即 d=2753。
n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）。

从新带入数字计算，看下，碉堡了；

以上程序和数字都是根据网上资料来的；不知哪儿错了；等有空再搞吧；

看程序可知，对于要加密的数字m, m^e%N=c, c就是加密之后的密文。c^d%N=m, 就能解密得到m