排序高级之交换排序_奇偶排序

奇偶排序，或奇偶换位排序，或砖排序，是一种相对简单的排序算法，最初发明用于有本地互连的并行计算。这是与冒泡排序特点类似的一种比较排序。

该算法中，通过比较数组中相邻的（奇-偶）位置数字对，如果该奇偶对是错误的顺序（第一个大于第二个），则交换。下一步重复该操作，但针对所有的（偶-奇）位置数字对。如此交替进行下去。

处理器数组的排序

在并行计算排序中，每个处理器对应处理一个值，并仅有与左右邻居的本地互连。所有处理器可同时与邻居进行比较、交换操作，交替以奇-偶、偶-奇的顺序。该算法由Habermann在1972年最初发表并展现了在并行处理上的效率。

该算法可以有效地延伸到每个处理器拥有多个值的情况。在Baudet–Stevenson奇偶合并分区算法中，每个处理器在每一步对自己所拥有的子数组进行排序，然后与邻居执行合并分区或换位合并。

Batcher奇偶归并排序

Batcher奇偶归并排序是一种相关但更有效率的排序算法，采用比较-交换和完美-洗牌操作。

Batcher的方法在拥有广泛互连的并行计算处理器上效率不错。

最差时间复杂度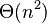

奇偶排序动态图：

代码实现：

package com.baobaotao.test;
/**
 * 排序研究
 * @author benjamin(吴海旭)
 * @email benjaminwhx@sina.com / 449261417@qq.com
 *
 */
public class Sort {
	/**
<span style="white-space:pre">	</span> * 奇偶排序
<span style="white-space:pre">	</span> * @param array
<span style="white-space:pre">	</span> */
	public static void batcherSort(int[] array) {
		int length = array.length ;
		boolean flag = true ;
		while(true) {
			flag = true ;
			for(int i=1;i<length-1;i+=2) {
				if(array[i] > array[i+1]) {
					swap(array, i, i+1) ;
					flag = false ;
				}
			}
			for(int i=0;i<length-1;i+=2) {
				if(array[i] > array[i+1]) {
					swap(array, i, i+1) ;
					flag = false ;
				}
			}
			if(flag) break ;
			printArr(array) ;
		}
	}
	/**
	 * 按从小到大的顺序交换数组
	 * @param a 传入的数组
	 * @param b 传入的要交换的数b
	 * @param c	传入的要交换的数c
	 */
	public static void swap(int[] a, int b, int c) {
		int temp = 0 ;
		if(b < c) {
			if(a[b] > a[c]) {
				temp = a[b] ;
				a[b] = a[c] ;
				a[c] = temp ; 
			}
		}
	}
	
	/**
	 * 打印数组
	 * @param array
	 */
	public static void printArr(int[] array) {
		for(int c : array) {
			System.out.print(c + " ");
		}
		System.out.println();
	}
	
	public static void main(String[] args) {
		int[] number={11,95,45,15,78,84,51,24,12} ;
		batcherSort(number) ;
	}
}

输出分析：

11 45 15 95 51 78 12 84 24 
11 15 45 51 12 95 24 78 84 
11 15 12 45 24 51 78 95 84 
11 12 15 24 45 51 78 84 95 

转载请注明：http://blog.csdn.net/benjamin_whx/article/details/42456755