4503: 两个串
Time Limit: 20 Sec Memory Limit: 256 MBSubmit: 630 Solved: 277
[Submit][Status][Discuss]
Description
Input
Output
Sample Input
a?aba?abba
Sample Output
HINT
不考虑通配符
这样如果s1和s2相等当且仅当f[x]=0
考虑有通配符的情况,把通配符的位置s2[i]=0
然后变换一下公式可得:
这个时候我们就可以利用FFT求卷积得到答案
如果没有理解呢~
来说一说卷积
括弧:资料来自[笔记]ACM笔记 - 利用FFT求卷积(求多项式乘法)
给定向量: a=(a0,a1,...,an−1) , b=(b0,b1,...,bn−1)
向量和:
a+b=(a0+b0,a1+b1,...,an−1+bn−1)
数量积(内积、点积):a⋅b=a0b0+a1b1+...+an−1bn−1
卷积:a⊗b=(c0,c1,...,c2n−2),其中
ck=∑i+j=k(aibj)
例如: cn−1=a0bn−1+a1bn−2+...+an−2b1+an−1b0
卷积的最典型的应用就是多项式乘法(多项式乘法就是求卷积)。
说一说FFT求卷积普通的计算多项式乘法的计算,时间复杂度 O(n2) 。而FFT先将多项式点值表示( O(nlogn) ),在 O(n) 下完成对点值的乘法,再以 O(nlogn) 完成IFFT,重新得到系数表示。
在两个多项式前面补0,得到两个2n次多项式,设系数向量分别为 v1 和 v2 。
使用FFT计算 f1=DFT(v1) 和 f2=DFT(v2) 。则 f1 与 f2 为两个多项式在 2n 次单位根处的取值(即点值表示)。
把 f1 与 f2 每一维对应相乘,得到 f ,代表对应输入多项式乘积的点值表示。
使用IFFT计算 v=IDFT(f) ,其中 v 就是乘积的系数向量。
a⊗b=IDFT2n(DFT2n(a)⋅DFT2n(b)) ,即: a⊗b=DFT−12n(DFT2n(a)⋅DFT2n(b))
这时我们再回过头来想题
只要把T串翻转,求一遍卷积,再扫一遍就好啦!
#include<cmath>
#include<ctime>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<complex>
#include<iostream>
#include<algorithm>
#include<iomanip>
#include<vector>
#include<string>
#include<bitset>
#include<queue>
#include<set>
#include<map>
#define pi acos(-1)
using namespace std;
typedef double db;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch<='9'&&ch>='0'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
void print(int x)
{if(x<0)putchar('-'),x=-x;if(x>=10)print(x/10);putchar(x%10+'0');}
const int N=140100;
complex<db>a[N],b[N],A[N],B[N],p[N];
int r[N];
void fft(complex<db> x[],int n,int t)
{
register int i,j,k,m;
for(i=0;i<n;++i)if(i<r[i])swap(x[i],x[r[i]]);
for(m=2;m<=n;m<<=1)
{
complex<db> wn(cos(2*pi*t/m),sin(2*pi*t/m));
for(i=0;i<n;i+=m)
{
complex<db> w(1,0),temp;k=m>>1;
for(j=0;j<k;++j,w*=wn)
{
temp=x[i+j+k]*w;
x[i+j+k]=x[i+j]-temp;
x[i+j]+=temp;
}
}
}
}
char s[N];
int st[N];
int main()
{
int n,len1,len2;
register int i,j;
scanf("%s",s);n=len1=strlen(s);for(i=0;i<len1;++i)a[i]=s[i]-'?';
scanf("%s",s+1);len2=strlen(s+1);for(i=0;i<len2;++i)b[i]=s[len2-i]-'?';
for(i=1,j=n;(i>>1)<j;i<<=1)n=i;
for(i=0;i<n;++i)r[i]=(i&1)*(n>>1)+(r[i>>1]>>1);
for(i=0;i<n;++i)B[i]=b[i]*b[i]*b[i];
for(i=0;i<n;++i)A[i]=1;
fft(A,n,1);fft(B,n,1);
for(i=0;i<n;++i)p[i]=A[i]*B[i];
for(i=0;i<n;++i)B[i]=b[i]*b[i];
for(i=0;i<n;++i)A[i]=complex<db>(2,0)*a[i];
fft(A,n,1);fft(B,n,1);
for(i=0;i<n;++i)p[i]-=A[i]*B[i];
for(i=0;i<n;++i)B[i]=b[i];
for(i=0;i<n;++i)A[i]=a[i]*a[i];
fft(A,n,1);fft(B,n,1);
for(i=0;i<n;++i)p[i]+=A[i]*B[i];
fft(p,n,-1);
for(i=0,j=0;i<=len1-len2;++i)if(p[i+len2-1].real()-0.5<0)st[++j]=i;
print(j);puts("");
for(i=1;i<=j;++i)print(st[i]),puts("");
return 0;
}
/*
bbabaababaaaaabaaaaaaaabaaabbbabaaabbabaabbbbabbbbbbabbaabbbababababbbbbbaaabaaabbbbbaabbbaabbbbabab
a?aba?abba
0
*/






 本文介绍了一种使用快速傅立叶变换(FFT)进行字符串匹配的方法,尤其针对含有通配符的模式串。通过将字符串转换为多项式并利用FFT进行卷积计算,实现了高效的匹配过程。
本文介绍了一种使用快速傅立叶变换(FFT)进行字符串匹配的方法,尤其针对含有通配符的模式串。通过将字符串转换为多项式并利用FFT进行卷积计算,实现了高效的匹配过程。
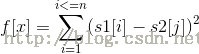
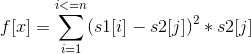
















 651
651

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








