这个题真有趣...
参考了http://www.cnblogs.com/jianglangcaijin/archive/2013/12/04/3457446.html,感觉这篇文章写得挺不错。
举个具体例子来说。
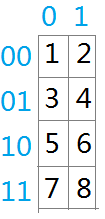
当a = 2,b = 1时,如图:
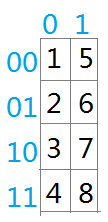
我们要将它转置为:
我们按二进制写下他们的坐标变化情况
我们发现:
1还在自己的位置。
2从001跑到了010,010原来的位置上是3,即2换到3。
3从010跑到了100,100原来的位置上是5,即3换到5。
4从011跑到了110,110原来的位置上是7,即4换到7。
同理,5换到2,6换到4,7换到6,8没有动。
显然这是一个置换,我们写出来:
我们发现这个置换的循环节为:
考虑循环节的性质,循环节内的所有点要调换到合适的位置,假设这个循环节有x个点,那么只需要调换x - 1次即可。
换句话说,如果有一个循环节,那么就可以少调换1次。
那么我们就有了思路:
每个点都需要调换一次,总共为2 ^ (a + b)次,但是因为循环节的存在,设循环节的个数为K的话,那么我们就可以少调换K次,答案就是2 ^ (a + b) - K。
前一项显然很好求,我们现在需要求K。
我们发现,在同一个循环节内的点,他们的二进制坐标可以通过向左平移a位(看成项链模型,不是<<)或者向右平移b位互相得到。(可以用笔写写其他情况,因为数据太大就不写出来了)
那么就可以具体为一个实际问题:
有一个由a + b个珠子串成的项链,有2种颜色(代表0和1),规定向左旋转a位(或向右旋转b位)为相同的项链,求不同的项链数。
但是这样似乎还是不好做,我们想把问题转化为”任意旋转都视为相同项链“的情况,这样我们就可以用Pólya了。于是再抽象一下。
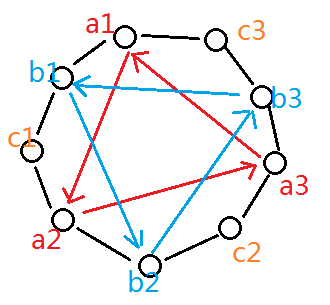
还是举个具体例子吧,假设此时a = 3,b = 6,有a + b = 9个珠子。
我们知道一个结论:移动a步,一共有gcd(a, a + b) = gcd(a, b)个循环节,每个循环节的长度都是(a + b) / gcd(a, b)。(这个证明详见我的另一篇文章:http://blog.csdn.net/braketbn/article/details/50669362)
我们人为给珠子标号,假设珠子是从a1, b1, c1开始旋转的,我们的思路是:
把a1, b1, c1看作一个大珠子,把a2, b2, c2看作下一个大珠子,以此例推就是把ai, bi, ci看做第i个大珠子。
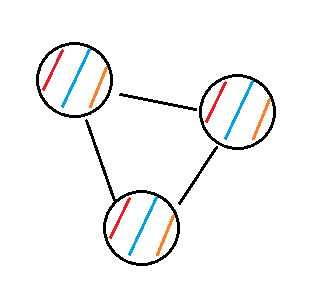
这样我们得到一个新项链
一共有(a + b) / gcd(a, b)个大珠子,每个大珠子都可以由2 ^ gcd(a, b)个颜色染色。
然后我们就把原问题转化成了一个等价的、熟悉的问题了。
Q:等等?为啥等价...?
A:一个大珠子的颜色其实代表了一个01串。具体来说,假设我们第一个大珠子的颜色是(红,蓝),那么a1和b1就被染上同种颜色,c1是另一种颜色。
大珠子的旋转1格相当于把原珠子对应的颜色旋转3格,满足原问题的条件,所以是完全等价的。
问题转化完毕,现在我们求K。
然后就是喜闻乐见的公式啦!
可以类比POJ2154(http://blog.csdn.net/acdreamers/article/details/8656247,这个文章写得不错)
令n = (a + b) / gcd(a, b),x = 2 ^ gcd(a, b)。
先用Pólya列出式子
用符号,化为
对gcd变形
从枚举k变为枚举k/d
注意第二个求和符号,刚好是欧拉函数的定义,变为
这就是最终的K...
phi怎么办?及时算?会TLE。于是要先用线性筛预处理出n以内的phi。
还有x...也要预处理出n以内的2的幂。
直接枚举d也会TLE,所以每次先把n质因数分解掉,dfs每个质因数的指数是多少,就可以枚举d了。
1/n的话求个逆元即可。
最后的答案是
完啦...
细节看代码。
#include <cstdio>
using namespace std;
typedef long long LL;
const int maxn = 1000001, p = 1000003;
int a, b, n, pow[maxn], phi[maxn], prime[maxn], cnt, fact[maxn], alpha[maxn], tot;
bool isnotprime[maxn];
inline int mul(int a, int b) {
return ((LL)a * b) % p;
}
inline int iread() {
int f = 1, x = 0; char ch = getchar();
for(; ch < '0' || ch > '9'; ch = getchar()) f = ch == '-' ? -1 : 1;
for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
return f * x;
}
void getphi() {
isnotprime[1] = 1; phi[1] = 1;
for(int i = 2; i < maxn; i++) {
if(!isnotprime[i]) prime[++cnt] = i, phi[i] = (i - 1) % p;
for(int j = 1; j <= cnt && i * prime[j] < maxn; j++) {
isnotprime[i * prime[j]] = 1;
if(i % prime[j] == 0) {
phi[i * prime[j]] = phi[i] * prime[j] % p;
break;
}
phi[i * prime[j]] = phi[i] * phi[prime[j]] % p;
}
}
}
void factor(int x) {
tot = 0;
for(int i = 1; i <= cnt && prime[i] * prime[i] <= n; i++) if(x % prime[i] == 0) {
++tot;
fact[tot] = prime[i];
for(alpha[tot] = 0; x % prime[i] == 0; x /= prime[i]) alpha[tot]++;
}
if(x > 1) ++tot, fact[tot] = x, alpha[tot] = 1;
}
int ans, L, g;
void dfs(int x, int d) {
if(d > tot) {
ans = (ans + mul(pow[x * g], phi[L / x])) % p;
return;
}
for(int i = 0; i <= alpha[d]; i++) {
dfs(x, d + 1);
x *= fact[d];
}
}
int gcd(int a, int b) {
for(; b; b ^= a ^= b ^= a %= b);
return a;
}
void exgcd(int a, int b, LL &x, LL &y) {
b ? (exgcd(b, a % b, y, x), y -= a / b * x) : (x = 1, y = 0);
}
int main() {
getphi();
pow[0] = 1; for(int i = 1; i < maxn; i++) pow[i] = (pow[i - 1] << 1) % p;
int T = iread();
while(T--) {
a = iread(); b = iread();
if(!a || !b) {
printf("0\n");
continue;
}
n = a + b;
g = gcd(a, b);
L = n / g; factor(L);
ans = 0;
dfs(1, 1);
LL x, y;
exgcd(L, p, x, y); x = (x % p + p) % p;
ans = mul(ans, x);
ans = pow[n] - ans; ans = (ans % p + p) % p;
printf("%d\n", ans);
}
return 0;
}











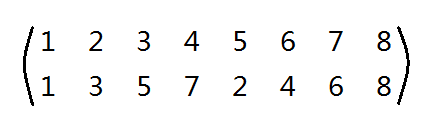
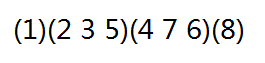
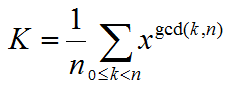
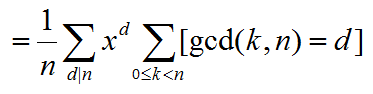
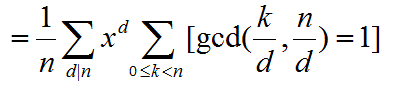
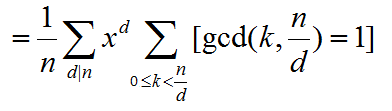
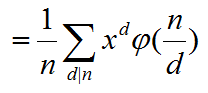
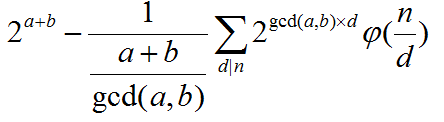













 331
331











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








