【ICPC-413】poj 2155 Matrix

点击打开poj 2155

思路: 二维树状数组+区间更新，单点查询

分析:

点击打开查看论文  建议先看看这篇论文，比较好理解

1 题目给定两种操作，第一种是给定左上角和右下角的下标，把这个子矩形里面的0/1进行互换，第二种是问某个点的值

2 我们先看一维的情况

 

假设题目给定的是一个长度为n的一维数组

那么我们现在要把区间[i,j]里面的值进行0/1互换

首先我们先来看一个定理，假设一个数原先为0，那么它经过奇数次的变换为1，偶数次的变换为0。

 

所以我们可以这么这么想[i,j]区间要变换那么就是相当于区间里面的值加1，那么等价于i这个点加1，j+1这个点减一

那么我们要判断某个点x的值的时候只要求出[1,x]的和mod2即可，为什么呢？

 

1 如果更新的区间是x的左边，那么对于x来说没有影响

2 如果x在更新的区间里面，那么就相当于加1

3 如果x在区间的右边，那么由于i加1，j减1那么抵消了

综上所述，可知结论成立

 

3 那么推广到二维的情况也是一样的

假设要更新的矩形的左上角为(x1,y1)，右下角为(x2,y2)

 

那么我们可以根据一维的思想推广到二维里面，那么我们就相当于(x1,y1)点加1，(x1,y2+1)点减1 ，(x2+1,y1)点减1 ，(x2+1 , y2+1)点加1

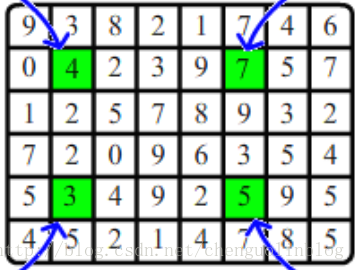
那么我们要求某个点(x,y)的值的时候也就相当于求点(1,1)到点(x,y)的矩形的值mod2

 

代码:

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int MAXN = 1010;

int treeNum[MAXN][MAXN];

int lowbit(int x){
    return x&(-x);
}

long long getSum(int x , int y){
    long long sum = 0;
    for(int i = x ; i > 0 ; i -= lowbit(i))
        for(int j = y ; j > 0 ; j -= lowbit(j))
            sum += treeNum[i][j];
    return sum;
}

void add(int x , int y , int val){
    for(int i = x ; i < MAXN ; i += lowbit(i))
        for(int j = y ; j < MAXN ; j += lowbit(j))
            treeNum[i][j] += val;
}

void solve(int m){
    char ch;
    int x , y;
    int x1 , y1 , x2 , y2;
    memset(treeNum , 0 , sizeof(treeNum));
    while(m--){ 
        scanf("%c" , &ch); 
        if(ch == 'C'){
            scanf("%d%d" , &x1 , &y1);
            scanf("%d%d%*c" , &x2 , &y2);
            // update
            add(x1 , y1 , 1);
            add(x2+1 , y1 , -1);
            add(x1 , y2+1 , -1);
            add(x2+1 , y2+1 , 1);
        }
        else{
            scanf("%d%d%*c" , &x , &y);
            int ans = getSum(x , y);
            printf("%d\n" , ans%2);
        }
    }
}

int main(){
    int cas;
    int n , m;
    bool isFirst = true;
    scanf("%d" , &cas);
    while(cas){
        scanf("%d%d%*c" , &n , &m); 
        solve(m);
        if(--cas)
            puts("");
    }
    return 0;
}