子图同构问题Ullmann 算法（二）

#目录索引

---

写在前面的话

以上的内容均出自这篇论文ullmann algorithm，所有的表述竟可能的和论文中的表述保持一致。 我要做的事情就是竟可能的讲的很清楚，尽可能的做到准确完备。

谨以此系列献给 my best love, grandpa~ 还有昆明宝石蓝的天空，2月的梨花，三月的樱花，10月的桂花，星光璀璨的星空陪我入梦乡，安静而又安抚人的环境，总是让我心很静，那些美好的事物总是想让我保持一颗干净温暖的内心。

要写点没有中国人写的，要搞点没有人做的事情才有意思，能做点推动中国计算机科学发展的事情，才有意义。老嚼别人吃过的东西，没有任何意义。不能推陈出新是件非常失败的事情。

这个世界是你们的，也是我的，终究还是我们的，这个世界不够完美不够好，一定是在等我们把它变美好！

还是那句话，focus on security! 认定好什么事情就要做到极致，做到很难被人超越。

---

---

#1.Ullmann算法的定义

1.1背景知识

对于图的同构问题，Ullmann 算法是一个简单的图同构算法，它采取的手段就是利用枚举找到子图同构。

这个算法的目的就是 对于一个给定的图Q，要找出在图G当中的和图Q同构的所有的子图。

用我们上一张的例子来说：

我们把左边的这个图叫做图A，右边的这个图叫做图B，那么我们要找出在图B中和图A同构的所有子图。

我们先找出几个看看。我们说过，子图同构就是根据点和边的关系，在另外一个图中找到对应的点，并且对应的点，边之间完全一样，就是存在相同的关联矩阵。

说明，我们考虑的还是不带标签的图，请忽略下面的A，B，C，D

当然我们举完全，你可以自己再看一下，但是绝对不像其他的博客当中说的只有两个，这是不对的。

Ullmann算法的基本思想我们在说一遍，就是要找到一个映射矩阵，然后找出这个映射矩阵对我们的图B做变换之后得到的矩阵中，只要图A的关联矩阵中数值为1的位置，对应的变换矩阵C也为1。

看不懂的看前一篇文章。

---

1.2 数学定义和描述

对于一个给定的图 $ G_{\alpha} = (V_{\alpha},E_{\alpha}) $ 和一个给定的图 $ G_{\beta}= (V_{\beta},E_{\beta}) $ ,我们的任务就是找出在$G_{\beta }$ 中和 $G_{\alpha }$ 同构的所有子图。 我们把在图
$G_{\alpha }=(V_{\alpha },E_{\alpha })$ 和 $ G_{\beta}= (V_{\beta},E_{\beta}) $ 的顶点数和边数分别记为 $ p_{\alpha} ,q_{\alpha}$ ；$p_{\beta },q_{\beta }$

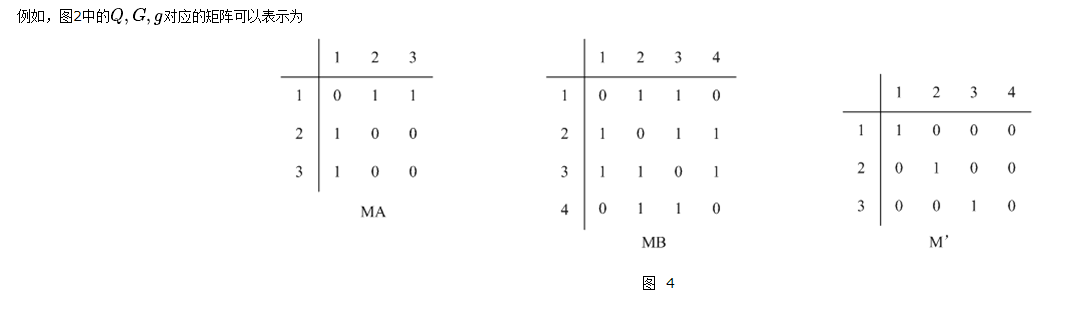
其中图 $ G_{\alpha} = (V_{\alpha},E_{\alpha}) $ 和 $ G_{\beta}= (V_{\beta},E_{\beta}) $ 的邻接矩阵 分别是$ A = [a_{ij}], B=[b_{ij}] $

之后我们定义一个映射矩阵$M^{{}^{\prime }}$ 它由 $ p_{\alpha} * p_{\beta} $ 个元素组成，其中每一行只能包含一个1，每一列至多只能包含一个1。我们通过这个矩阵 $M^{{}^{\prime }}$ 要对矩阵 $B$进行一系列的行列变换，得到我们的矩阵 $C$ , 我们的矩阵C定义如下：

$$C=[C_{ij}]=M^{{}^{\prime }}(M^{{}^{\prime }}B{)}^T$$

其中T是表示矩阵的转置。

如果在图B中有图A的同构矩阵，那么一定满足：

那么 $ M^{’}$就指出了 图 $G_{\alpha }=(V_{\alpha },E_{\alpha })$ 和 $ G_{\beta}= (V_{\beta},E_{\beta}) $ 的一个同构映射

---

为啥我的CSDN的latex的代码显示出来的东西为啥总是后面有条线。为啥？？？？

本小节涉及到Latex代码：

$ G_{\alpha} = (V_{\alpha},E_{\alpha}) $
$G_{\beta}= (V_{\beta},E_{\beta})$
$G_{\beta}$
$G_{\alpha}$ 

$$C = [C_{ij}] = M^{'} (M^{'}B)^{T}  $$ 

---

---

#2.Ullmann算法实现

对于Ullman算法的主要目的就是找到我们的 $ M^{’} $

开始的时候我们先定义一个矩阵， $M^{0} $ 这个矩阵由 $ p_{\alpha} *p_{\beta} $ 个元素构成

其中这个矩阵中为1的元素满足B这个图中的度大于等于A中元素的度。现在我们就来构建这个初始的矩阵$M^{0} $。

我们还是以我们的那个例子来说明：

构建我们的M0这个矩阵。

可以发现在图A中，每个顶点的度都是小于图B中任何顶点的度。所以这个矩阵的初始矩阵应该全是1。

这个怎么看，我们的矩阵的行表示的是我们的图A各个顶点，列表示的我们的图B的每个点。

先看第一行，A的元素都是小于或者等于B中的每个元素的度，以此类推，构成这个矩阵。

然后我们要得到最后的映射矩阵，对这个初始矩阵M0进行变换，使得最后每一行有且只有一个1，每一列最多只有一个1。这样就找到我们的矩阵。之后按照定理1算矩阵C看和A之间额对应关系。

算法如下：

update@2016-10-8 19：55

在这个算法中使用了两个二进制的向量 $\vec{F}$ 和$\vec{H}$

我们要找一个映射矩阵 $M^{{}^{\prime }}$, 这个矩阵由 $p_{\alpha }$行 $ p_{\beta}$列，我们的初始矩阵是$M^{{0}$和我们的$M}{’}$大小是一致的。我们就是要将 $M^0$一步一步变换到我们需要的 $M^{{}^{\prime }}$矩阵。

这个深度d其实就是我们运算到了哪一行

$H_d=k$表示的是运算到第d行的时候（当深度为d）的时候第k列已经被用了。

下面我们亲自实践一下整个算法的运算过程。

首先执行算法的第一部，初始矩阵 $M^0$赋值给矩阵M

设置遍历深度为1，H1=0

设置向量F的前 $p_{\alpha }$都为0

就这样我们就找到了一个我们需要的映射矩阵，这个时候按照定理1，我们发现找到了我们需要的矩阵C，在不断枚举和验证我们可以找到其他的映射矩阵。

这个就是我们的Ullmann算法的实现的基本思想。

今天就更新到这里了，滚回去学习了。

有啥大家一起交流吧~~~

biubiu~~~

---

---

写在后面的话

无意中发现了一个巨牛的人工智能教程，忍不住分享一下给大家。教程不仅是零基础，通俗易懂，而且非常风趣幽默，像看小说一样！觉得太牛了，所以分享给大家。点这里可以跳转到教程 https://www.captainbed.net/chichoxian

我望着碧海蓝天
　　看云朵在兜圈
　　慢慢兜成你的淘气鬼脸
　　忽近忽远woo……
　　微风在摇手轻吹
　　阳光睡在我的右侧脸
　　我笑着脸去迎接
　　你给的誓言yeah……
　　没发现紫外线太强烈
　　我爱你没有防备
　　等你牵手带着我漫游世界
幸福快乐瞬间一起体会
　　后知后觉地逃远
　　我们躲在秘密的空中花园
　　爱情蝴蝶也和我们相约
　　夜色倒垂还看你更沉睡
　　只怕还不够爱time’s going by
　　oh~yeah……