题目原文:
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
题目大意:
你在爬一个n阶的楼梯,每次可以上1阶也可以上2阶。有多少种不同的爬法?
题目分析:
设爬n阶的楼梯不同的方法是f(n),则最后一次可以爬1阶也可以爬2阶。因此f(n)=f(n-1)+f(n-2).这个公式很熟悉吧。。没错此题即是求斐波那契数列的n+1项。为什么是n+1项呢,因为斐波那契数列是1,1,2,3,….而爬楼梯问题的方法数是1,2,3,5…
源码:(language:c)
int climbStairs(int n) {
int i,sum1=1,sum2=2,sum=0;
if(n==1||n==2)
return n;
else {
for(i=2;i<n;i++) {
sum=sum1+sum2;
sum1=sum2;
sum2=sum;
}
return sum;
}
}成绩:
0ms,beats0.16% 众数0ms,99.84%.
Cmershen的碎碎念:
求斐波那契数列切勿用递推公式f(n)=f(n-1)+f(n-2),会引起超时。因为随着n的增加会大量出现重复计算,使用递推的算法复杂度是NP难的,而本算法是O(n)复杂度的。如果使用斐波那契的通项公式(什么?你不知道斐波那契可以求通项?回去复习高中数学一百遍!)算法复杂度可降低到O(1),但通项中的系数是无理数,在计算机中不易表示。
斐波那契数列通项公式如下:








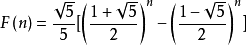














 176
176

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








