3.8求二叉树中节点的最大距离

题目：

写一个程序求一棵二叉树中相距最远的两个节点之间的距离。

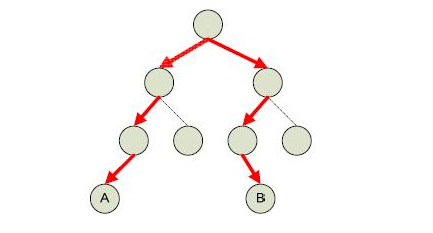
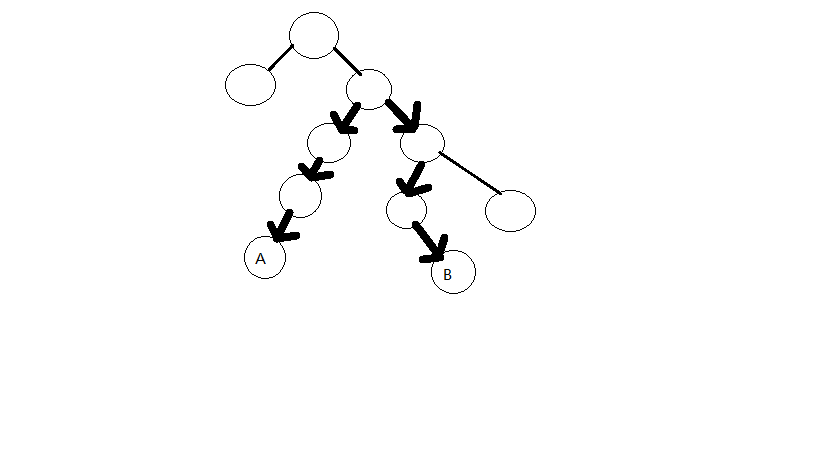
粗箭头的边表示最长距离。

分析：

相距最远的两个节点，一定是两个叶子节点，或者是一个叶子节点到它的根节点（单枝树）。

我们来考虑相距最远的两个节点是两个叶子节点的情况。

对于任意一个节点，以该节点为根，假设这个根有k个孩子节点，那么相距最远的两个节点U和V之间的路径与这个根节点的关系有两种情况。

1.若路径经过根节点，那么节点U和V属于两个不同的子树。那么就有U和V都是它们所在子树到根节点最远的节点。

2.若路径不经过根节点：

那么节点U和V一定属于根节点的k个子树之一。同时满足，它们是子树中相距最远的两个节点。

此时问题就能转化成在子树上的解，用动态规划，自底向上。
树R有k棵子树
设第k棵子树中相距最远的两个节点: Uk和Vk。
d(Uk,Vk)为子树k的最大距离。
假设Uk为子树k中到子树k的根节点Rk的距离最长的节点。
那么其到树的根节点R的距离定义为d(Uk,R)。
选出d(Ui,R)(1≤i≤k)中最大的两个值max1,max2,那么经过根节点R的最长路径为max1+max2+1。
所以树R中相距最远的两个节点的距离为：
max{d(U1,V1),d(U2,V2)…,d(Uk,Vk),max1+max2+1}。

代码：

#include<iostream>
#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
using namespace std;
struct TreeNode{
    char val;
    TreeNode* left;
    TreeNode* right;
    int maxLenLeft;//左子树到父亲节点的最大长度
    int maxLenRight;
    TreeNode(char x) :val(x), left(NULL), right(NULL), maxLenLeft(0), maxLenRight(0){

    }
};

void createBinaryTree(TreeNode* &root){
    char ch;
    cin >> ch;
    if (ch == '#'){
        return;
    }
    root = new TreeNode(ch);
    createBinaryTree(root->left);
    createBinaryTree(root->right);
}
//递归
void findMaxLen(TreeNode* root,int &maxLen){
    if (root != NULL){
        findMaxLen(root->left,maxLen);
        findMaxLen(root->right,maxLen);
        if (root->left != NULL){
            root->maxLenLeft = max(root->left->maxLenLeft + 1, root->left->maxLenRight + 1);
        }
        if (root->right != NULL){
            root->maxLenRight = max(root->right->maxLenLeft + 1, root->right->maxLenRight + 1);
        }
        maxLen = max(maxLen,root->maxLenLeft+root->maxLenRight+1);
    }
}
//非递归
void findMaxLen_Nonrecursive(TreeNode* root,int &maxLen){
    stack<TreeNode*> s;
    TreeNode* cur = root;
    TreeNode* pre = NULL;
    while (cur != NULL || !s.empty()){
        while (cur != NULL){
            s.push(cur);
            cur = cur->left;
        }
        cur = s.top();
        //如果当前节点的右孩子为空，或者右孩子被访问过，那么访问当前节点
        if (cur->right == NULL || cur->right == pre){
            if (cur->left != NULL){
                cur->maxLenLeft = max(cur->left->maxLenLeft+1,cur->left->maxLenRight+1);
            }
            if (cur->right != NULL){
                cur->maxLenRight = max(cur->right->maxLenLeft+1,cur->right->maxLenRight+1);
            }
            maxLen = max(maxLen,cur->maxLenLeft+cur->maxLenRight+1);
            s.pop();
            pre = cur;
            cur = NULL;
        }
        else{
            cur = cur->right;
        }
    }
}