UVa: 1595 - Symmetry

最新推荐文章于 2021-04-12 19:04:07 发布

crazy__chen

最新推荐文章于 2021-04-12 19:04:07 发布

阅读量1.2k

点赞数

CC 4.0 BY-SA版权

分类专栏： java 算法与数据结构

本文链接：https://blog.csdn.net/crazy__chen/article/details/43544079

java 同时被 2 个专栏收录

75 篇文章

订阅专栏

算法与数据结构

73 篇文章

订阅专栏

本文探讨如何在平面上的点集中找到一条竖线，使得所有点左右对称。通过两种思路实现这一目标，包括计算对称轴并检查每个点的对称点是否存在，以及暴力枚举对称轴的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：给出平面上N(N<=1000)个点。问是否可以找到一条竖线，使得所有点左右对称，如图所示：

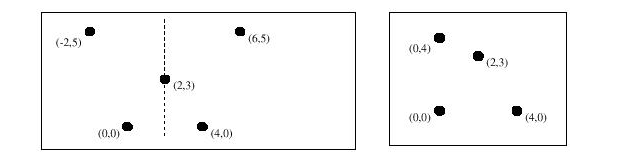
则左边的图形有对称轴，右边没有。

思路1：如点集存在对称轴，则对称轴为点集x坐标和的平均。然后用set存储每个点(输入点不同),遍历每一个点，通过求得的对称轴，计算它的对称点，若不存在则输出“NO”。
思路2：暴力枚举，如果存在对称轴的话那么对称轴的横坐标一定是最左边的点和最右边的点的中点为了避免中点是小数可以将横坐标都乘上2 然后在判断所有点是否有对称点就行了
下面实现思路1

package test;

import java.util.HashSet;

public class Test{
	
	private static class Point{
		int x;
		int y;
		public Point(int x, int y) {
			super();
			this.x = x;
			this.y = y;
		}
		
		@Override
		public boolean equals(Object obj) {
			Point o = (Point) obj;
			if(x==o.x && y==o.y)
				return true;
			else 
				return false;
		}
		
		@Override
		public String toString() {			
			return x+","+y;
		}
		
		@Override
		public int hashCode() {
			return 10000*x+y;
		}
	}
	
	static HashSet<Point> points = new HashSet<Point>();
	
	public static void main(String[] args) {
		//测试数据
		points.add(new Point(-2, 5));
		points.add(new Point(6, 5));
		points.add(new Point(2, 3));
		points.add(new Point(0, 0));
		points.add(new Point(4, 0));
						
		int sum = 0;
		for(Point point : points){
			sum += point.x;
		}
		sum = sum/points.size();//这个就是对称轴
		
		//检查每个点是否存在对称点
		for(Point point : points){
			if(!points.contains(new Point(sum*2-point.x, point.y))){
				System.out.println("不对称");
				System.exit(0);				
			}
		}
		System.out.println("对称");
	}          
}