算法导论分而治之学习笔记

The divide-and-conquer design paradigm

1. Divide the problem (instance)

into subproblems.

2. Conquer the subproblems by

solving them recursively.

3. Combine subproblem solutions.

merge sort

1. Divide: Trivial.

2. Conquer: Recursively sort 2 subarrays.

3. Combine: Linear-time merge.

Master theorem (reprise)

T(n) = aT(n/b) + f (n)

CASE 1: f (n) = O(nlogba –ε)

⇒ T(n) = Θ(nlogba) .

CASE 2: f (n) =Θ(nlogba lgkn)

⇒ T(n) = Θ(nlogba lgk+1n) .

CASE 3: f (n) = Ω(nlogba +ε) and a f (n/b) ≤ c f (n)

⇒ T(n) = Θ( f (n)) .

Merge sort: a = 2, b = 2 ⇒ nlogba = n⇒ CASE 2 (k = 0) ⇒ T(n) = Θ(n lg n) .

Binary search

1. Divide: Check middle element.

2. Conquer: Recursively search 1 subarray.

3. Combine: Trivial.

Recurrence for binary search

nlogba = nlog21 = n0 = 1⇒ CASE 2 (k = 0)⇒ T(n) = Θ(lg n) .

Powering a number

Problem: Compute, where n ∈ N.

Naive algorithm: Θ(n).

Divide-and-conquer algorithm:

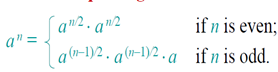
T(n) = T(n/2) + Θ(1) . T(n) = Θ(lg n) .

Fibonacci numbers

Recursive definition:

0 1 1 2 3 5 8 13 21 34 ….

Naive recursive algorithm: Ω()

(exponential time), where φ =( )/2 is the golden ratio.

Computing Fibonacci numbers

Naive recursive squaring:

Fn = /

rounded to the nearest integer.

• Recursive squaring: Θ(lg n) time.

• This method is unreliable, since floating-point

arithmetic is prone to round-off errors.

Bottom-up

• Compute F0, F1, F2, …, Fn in order, forming

each number by summing the two previous.

• Running time: Θ(n).

Recursive squaring

Theorem:

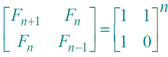
Algorithm: Recursive squaring.Time = Θ(lg n) .

Proof of theorem. (Induction on n.)

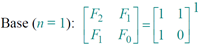
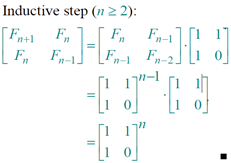
Matrix multiplication

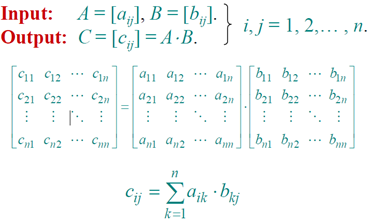
Standard algorithm

for i ← 1 to n

do for j ← 1 to n

do cij ← 0

for k ← 1 to n

do cij ← cij + aik⋅ bkj

Running time = Θ(n3)

Divide-and-conquer algorithm

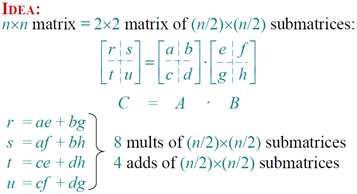
Analysis of D&C algorithm

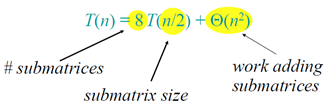
nlogba = nlog28 = n3 ⇒ CASE 1 ⇒ T(n) = Θ(n3).

No better than the ordinary algorithm.

Strassen's idea

• Multiply 2×2 matrices with only 7 recursive mults.

P1 = a ⋅ ( f – h)

P2 = (a + b) ⋅ h

P3 = (c + d) ⋅ e

P4 = d ⋅ (g – e)

P5 = (a + d) ⋅ (e + h)

P6 = (b – d) ⋅ (g + h)

P7 = (a – c) ⋅ (e + f )

 

r = P5 + P4 – P2 + P6

s = P1 + P2

t = P3 + P4

u = P5 + P1 – P3 – P7

 

7 mults, 18 adds/subs.

Note: No reliance on

commutativity of mult!

Strassen's algorithm

1. Divide: Partition A and B into

(n/2)×(n/2) submatrices. Form terms

to be multiplied using + and – .

2. Conquer: Perform 7 multiplications of

(n/2)×(n/2) submatrices recursively.

3. Combine: Form C using + and – on

(n/2)×(n/2) submatrices.

T(n) = 7 T(n/2) + Θ(n2)

 

Analysis of Strassen

T(n) = 7 T(n/2) + Θ(n2)

nlogba = nlog27 ≈ n2.81 ⇒ CASE 1 ⇒ T(n) = Θ(nlg 7).

The number 2.81 may not seem much smaller than

3, but because the difference is in the exponent, the

impact on running time is significant. In fact,

Strassen's algorithm beats the ordinary algorithm

on today's machines for n ≥ 30 or so.on today's machines for n ≥ 30 or so.

on today's machines for n ≥ 30 or so.

VLSI layout

Problem: Embed a complete binary tree

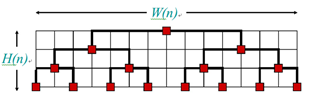
H(n) = H(n/2) + Θ(1) W(n) = 2 W(n/2) + Θ(1)

= Θ(lg n)= Θ(n)

with n leaves in a grid using minimal area.

Area = Θ(n lg n)