【剑指Offer学习】【面试题25：二叉树中和为某一值的路径】

题目：输入一棵二叉树和一个整数， 打印出二叉树中结点值的和为输入整数的所有路径。从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

---

二叉树结点的定义：

public static class BinaryTreeNode {
    int value;
    BinaryTreeNode left;
    BinaryTreeNode right;
}

解题思路：

由于路径是从根结点出发到叶结点， 也就是说路径总是以根结点为起始点，因此我们首先需要遍历根结点。在树的前序、中序、后序三种遍历方式中，只有前序遍历是首先访问根结点的。

当用前序遍历的方式访问到某一结点时， 我们把该结点添加到路径上，并累加该结点的值。如果该结点为叶结点并且路径中结点值的和刚好等于输入的整数， 则当前的路径符合要求，我们把它打印出来。如果当前结点不是叶结点，则继续访问它的子结点。当前结点访问结束后，递归函数将自动回到它的父结点。因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值，以确保返回父结点时路径刚好是从根结点到父结点的路径。

不难看出保存路径的数据结构实际上是一个枝， 因为路径要与递归调用状态一致， 而递归调用的本质就是一个压栈和出栈的过程。

代码实现：

public class Test25 {
    /**
     * 二叉树的树结点
     */
    public static class BinaryTreeNode {
        int value;
        BinaryTreeNode left;
        BinaryTreeNode right;
    }

    /**
     * 输入一棵二叉树和一个整数， 打印出二叉树中结点值的和为输入整数的所有路径。
     * 从树的根结点开始往下一直到叶销点所经过的结点形成一条路径。
     *
     * @param root        树的根结点
     * @param expectedSum 要求的路径和
     */
    public static void findPath(BinaryTreeNode root, int expectedSum) {
        // 创建一个链表，用于存放根结点到当前处理结点的所经过的结点
        List<Integer> list = new ArrayList<>();

        // 如果根结点不为空，就调用辅助处理方法
        if (root != null) {
            findPath(root, 0, expectedSum, list);
        }
    }

    /**
     * @param root        当前要处理的结点
     * @param curSum      当前记录的和（还未加上当前结点的值）
     * @param expectedSum 要求的路径和
     * @param result      根结点到当前处理结点的所经过的结点，（还未包括当前结点）
     */
    public static void findPath(BinaryTreeNode root, int curSum, int expectedSum, List<Integer> result) {

        // 如果结点不为空就进行处理
        if (root != null) {
            // 加上当前结点的值
            curSum += root.value;
            // 将当前结点入队
            result.add(root.value);
            // 如果当前结点的值小于期望的和
            if (curSum < expectedSum) {
                // 递归处理左子树
                findPath(root.left, curSum, expectedSum, result);
                // 递归处理右子树
                findPath(root.right, curSum, expectedSum, result);
            }
            // 如果当前和与期望的和相等
            else if (curSum == expectedSum) {
                // 当前结点是叶结点，则输出结果
                if (root.left == null && root.right == null) {
                    System.out.println(result);
                }
            }
            // 移除当前结点
            result.remove(result.size() - 1);
        }
    }

    public static void main(String[] args) {
        //            10
        //         /      \
        //        5        12
        //       /\
        //      4  7
        BinaryTreeNode root = new BinaryTreeNode();
        root.value = 10;
        root.left = new BinaryTreeNode();
        root.left.value = 5;
        root.left.left = new BinaryTreeNode();
        root.left.left.value = 4;
        root.left.right = new BinaryTreeNode();
        root.left.right.value = 7;
        root.right = new BinaryTreeNode();
        root.right.value = 12;

        // 有两条路径上的结点和为22
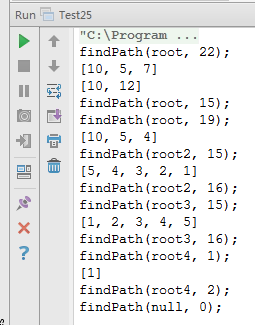
        System.out.println("findPath(root, 22);");
        findPath(root, 22);

        // 没有路径上的结点和为15
        System.out.println("findPath(root, 15);");
        findPath(root, 15);

        // 有一条路径上的结点和为19
        System.out.println("findPath(root, 19);");
        findPath(root, 19);


        //               5
        //              /
        //             4
        //            /
        //           3
        //          /
        //         2
        //        /
        //       1
        BinaryTreeNode root2 = new BinaryTreeNode();
        root2.value = 5;
        root2.left = new BinaryTreeNode();
        root2.left.value = 4;
        root2.left.left = new BinaryTreeNode();
        root2.left.left.value = 3;
        root2.left.left.left = new BinaryTreeNode();
        root2.left.left.left.value = 2;
        root2.left.left.left.left = new BinaryTreeNode();
        root2.left.left.left.left.value = 1;

        // 有一条路径上面的结点和为15
        System.out.println("findPath(root2, 15);");
        findPath(root2, 15);

        // 没有路径上面的结点和为16
        System.out.println("findPath(root2, 16);");
        findPath(root2, 16);

        // 1
        //  \
        //   2
        //    \
        //     3
        //      \
        //       4
        //        \
        //         5
        BinaryTreeNode root3 = new BinaryTreeNode();
        root3.value = 1;
        root3.right = new BinaryTreeNode();
        root3.right.value = 2;
        root3.right.right = new BinaryTreeNode();
        root3.right.right.value = 3;
        root3.right.right.right = new BinaryTreeNode();
        root3.right.right.right.value = 4;
        root3.right.right.right.right = new BinaryTreeNode();
        root3.right.right.right.right.value = 5;

        // 有一条路径上面的结点和为15
        System.out.println("findPath(root3, 15);");
        findPath(root3, 15);

        // 没有路径上面的结点和为16
        System.out.println("findPath(root3, 16);");
        findPath(root3, 16);

        // 树中只有1个结点
        BinaryTreeNode root4 = new BinaryTreeNode();

        root4.value = 1;
        // 有一条路径上面的结点和为1
        System.out.println("findPath(root4, 1);");
        findPath(root4, 1);

        // 没有路径上面的结点和为2
        System.out.println("findPath(root4, 2);");
        findPath(root4, 2);

        // 树中没有结点
        System.out.println("findPath(null, 0);");
        findPath(null, 0);
    }
}

运行结果：