【编程马拉松算法目录】
【019-一笔画】【工程下载>>>】
1 题目描述
咱们来玩一笔画游戏吧,规则是这样的:有一个连通的图,能否找到一个恰好包含了所有的边,并且没有重复的路径。
1.1 输入描述:
输入包含多组数据。每组数据的第一行包含两个整数n和m (2≤n, m≤1000),其中n是顶点的个数,m是边的条数。紧接着有m行,每行包含两个整数from和to (1 ≤ from, to ≤ n, from != to),分别代表边的两端顶点。边是双向的,并且两个顶点之间可能不止一条边。
1.2 输出描述:
对应每一组输入,如果能一笔画则输出“Yes”;否则输出“No”。
1.3 输入例子:
3 3
1 2
2 3
1 3
4 7
1 2
2 1
1 3
1 4
1 4
2 3
4 3
1.4 输出例子:
Yes
No
2 解题思路
题目要求一个连通的有向图是否可以一笔画完。这是一个可行遍性问题,即从图中一个顶点出发不重复地遍历完所有的边并回到起始顶点,这种回路是欧拉回路。在解答该问题前先对欧拉回路相关的内容进行介绍。
2.1 欧拉回路
2.1.1 欧拉通路、欧拉回路、欧拉图
无向图:
1) 设G 是连通无向图,则称经过G 的每条边一次并且仅一次的路径为欧拉通路;
2) 如果欧拉通路是回路(起点和终点是同一个顶点),则称此回路为欧拉回路(Euler circuit);
3) 具有欧拉回路的无向图G 称为欧拉图(Euler graph)。
有向图:
1) 设D是有向图,D的基图连通,则称经过D的每条边一次并且仅一次的有向路径为有向欧拉通路;
2) 如果有向欧拉通路是有向回路,则称此有向回路为有向欧拉回路(directed Euler circuit);
3) 具有有向欧拉回路的有向图D称为有向欧拉图(directed Euler graph)。
图1是有向图。

图1 有向图和无向图
2.1.2 定理及推论
欧拉通路和欧拉回路的判定是很简单的,请看下面的定理及推论。
定理2.1 无向图G存在欧拉通路的充要条件是:
G为连通图,并且G仅有两个奇度结点(度数为奇数的顶点)或者无奇度结点。
推论2.1:
1) 当G是仅有两个奇度结点的连通图时,G的欧拉通路必以此两个结点为端点。
2) 当G是无奇度结点的连通图时,G必有欧拉回路。
3) G为欧拉图(存在欧拉回路)的充分必要条件是G为无奇度结点的连通图。
例如图1(a)所示的无向图,存在两个奇度顶点v2和v5,所以存在欧拉通路,且欧拉通路必以这两个顶点为起始顶点和终止顶点;该无向图不存在欧拉回路。图2-1(b)所示的无向图为欧拉图。
定理2.2 有向图D存在欧拉通路的充要条件是:
D为有向图,D的基图连通,并且所有顶点的出度与入度都相等;或者除两个顶点外,其余顶点的出度与入度都相等,而这两个顶点中一个顶点的出度与入度之差为1,另一个顶点的出度与入度之差为-1。
推论2.2:
1) 当D除出、入度之差为1,-1的两个顶点之外,其余顶点的出度与入度都相等时,D的有向欧拉通路必以出、入度之差为1的顶点作为始点,以出、入度之差为-1的顶点作为终点。
2) 当D的所有顶点的出、入度都相等时,D中存在有向欧拉回路。
3) 有向图D为有向欧拉图的充分必要条件是D的基图为连通图,并且所有顶点的出、入度都相等。
例如图1(c)所示的有向图,顶点v2和v4入度和出度均为1;顶点v1的出度为2、入度为1,二者差值为1;顶点v3的出度为1、入度为2,二者相差为-1;所以该有向图只存在有向欧拉通路,且必须以顶点v1为始点,以顶点v3为终点。图1(d)所示的有向图不存在有向欧拉通路。
2.2 解题步骤
首先根据输入构造图的邻接矩阵,通过邻接矩阵判断图是否连通,不连通说明不可以一笔画完,如果连通,再判断图是否有奇度顶点,有就不能一笔画完,没有就说明可以一笔画完。
3 算法实现
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
/**
* Author: 王俊超
* Time: 2016-05-12 09:04
* CSDN: http://blog.csdn.net/derrantcm
* Github: https://github.com/Wang-Jun-Chao
* Declaration: All Rights Reserved !!!
*/
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Scanner scanner = new Scanner(Main.class.getClassLoader().getResourceAsStream("data3.txt"));
while (scanner.hasNext()) {
int n = scanner.nextInt();
int m = scanner.nextInt();
// 记录边
int[] edge = new int[m * 2];
for (int i = 0; i < edge.length; i++) {
edge[i] = scanner.nextInt();
}
if (draw(n, edge)) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
scanner.close();
}
/**
* 图是否可以笔画完(判断无向图是否存在欧拉通路)
*
* @param n 顶点点个数,顶点的编号从1到n
* @param edge 边的连接数组,两个一起表示一条边
* @return true:可以一笔画完,false:不可以一笔画完
*/
private static boolean draw(int n, int[] edge) {
int[] vertex = new int[n + 1];
// 统计每个顶点的度数
for (int i : edge) {
vertex[i]++;
}
///////////////////////////////////////////////////////////////////////////////////////////
// 无向图G存在欧拉通路的充要条件是:G为连通图,并且G仅有两个奇度结点(度数为奇数的顶点)或者无奇度结点。
///////////////////////////////////////////////////////////////////////////////////////////
// 统计奇度顶点个数
int count = 0;
for (int i = 1; i < vertex.length; i++) {
if (vertex[i] % 2 != 0) {
count++;
}
}
// 奇度顶点不为0且不为2说明不存在欧拉通路
if (count != 0 && count != 2) {
return false;
}
// 构造边的邻接矩阵
int[][] graph = new int[n + 1][n + 1];
for (int i = 0; i < edge.length; i += 2) {
int v = edge[i];
int w = edge[i + 1];
graph[v][w]++;
graph[w][v]++;
}
// 清空顶号入度标记,将它作为访问标记使用,0表示没有访问过,1表示访问过
for (int i = 0; i < vertex.length; i++) {
vertex[0] = 0;
}
List<Integer> list = new ArrayList<>(n);
// 有向图连通,那么从任意一个顶点都可以访问到其它的顶点
// 从第一个顶点开始访问,进行广度优先遍历
vertex[1] = 1;
list.add(1);
while (!list.isEmpty()) {
int v = list.remove(0);
for (int i = 1; i <= n; i++) {
// 边(v, i),t为0说明v不能直接到i
int t = graph[v][i];
// 如果(v, i)可达,且顶点i没有被访问过,就标记已经访问过,添加到访问队列中
if (t != 0 && vertex[i] == 0) {
vertex[i] = 1;
list.add(i);
}
}
}
for (int i = 1; i < vertex.length; i++) {
// 还有顶点没有访问到,说明图不连通
if (vertex[i] == 0) {
return false;
}
}
return true;
}
}
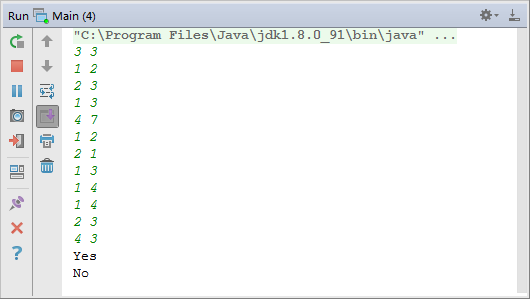
4 测试结果
5 其它信息
因为markddow不好编辑,因此将文档的图片上传以供阅读。Pdf和Word文档可以在Github上进行【下载>>>】。
























 634
634

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








