树

最新推荐文章于 2021-10-29 21:01:00 发布

disappearedgod

最新推荐文章于 2021-10-29 21:01:00 发布

阅读量1.2k

点赞数

分类专栏：树字符串(String) 数据结构文章标签：数据结构树 String

本文链接：https://blog.csdn.net/disappearedgod/article/details/24422297

版权

树同时被 3 个专栏收录

34 篇文章 0 订阅

订阅专栏

数据结构

27 篇文章 0 订阅

订阅专栏

字符串(String)

25 篇文章 0 订阅

订阅专栏

作者：disappearedgod

文章出处：http://blog.csdn.net/disappearedgod/article/details/24422297

时间：2014-4-24

前记

原博客：数据结构-树由于内容太多不好管理，先把原来的内容按照一级标题分解开来，便于查看和修改。

0 树

0.1 树的概念

定义：

树是一种数据结构，表示为TREE=（D，R）；
其中：D是具有相同特性的数据元素的集合；R是元素集合D上的关系集合，如果D中只含有一个数据元素，则R为空集。

或者用递归定义为：
树是N（N>0）个结点的有限集合，其唯一关系具有下列属性：
集合中存在唯一的一个结点，称为树根，该结点没有前驱；

除根结点外，其余结点分为M（M≥0）个互不相交的集合，其中每一个集合都是一棵树，并称其为根的子树。

（一个小注释：查找某一个存在节点的前驱和后继。某一个节点x的后继就是大于key[x]的关键字中最小的那个节点，前驱就是小于key[x]的关键字中最大的那个节点。）

0.2 基本术语

一个结点的子树个数称为该结点的度（degree）
一棵树中结点度的最大值称为该树的度
度为零的结点称为叶子（leaf）或者终端结点
度不为零的结点称为分支结点或者非终端结点
除根结点之外的分支结点统称为内部结点
树中结点的后继结点称为儿子（child）或者子结点，简称儿子
结点的前驱结点称为儿子的双亲（parents）或者父结点，简称父亲
同一个父亲的儿子互称为兄弟（sibling）
若树中存在一个结点序列k1k2k3…kj，使得ki是ki+1的父亲（1≤i＜j），则称该结点序列是从k1到kj的一条路径（path）或者道路
路径的长度等于j-1，它是该路径所经过的边（即连接两个结点的线段）的数目
若树中结点k到ks存在一条路径，则称k是ks的祖先（Ancestor），ks是k的子孙（Descendant）
结点的层数（level）是从根开始算起的。设根结点的层数为1，其余结点的层数等于其父亲结点的层数加1，树中结点的最大层数称为树的高度（Height）或者深度（Depth）
若把树中每个结点的各子树看成从左到右有次序的（即不能互换），则称该树为有序树（Ordered Tree）；否则称为无序树（Unordered Tree）

森林（Forest）是m（m≥0）棵互不相交树的集合。树形结构是非线性结构。祖先与子孙的关系则是对父子关系的延伸，其定义了树中结点的纵向次序。如果规定k1和k2是兄弟，且k1在k2的左边，则k1的任一子孙都在k2的任一子孙的左边，则定义了树中结点的横向次序

0.3 树的遍历

树的遍历是树中每个节点仅访问一次的过程。

遍历的定义只指定了一个条件：每个节点仅访问一次，没有指定这些节点的访问顺序。因此，节点有多少种排序方式，就有多少种排序方式，就有多少种遍历方式。

0.3.1．先根遍历

先根遍历的定义为：
(1) 访问根结点；
(2) 按照从左到右的顺序先根遍历根结点的每一棵子树。

0.3.2．后根遍历

后根遍历的定义为：
(1) 按照从左到右的顺序后根遍历根结点的每一棵子树；

(2) 访问根结点。

0.3.3 广度优先遍历

广度优先遍历从最底层（或者最高层）开始，向下（或向上）逐层访问每个节点，在每一层次上，从左到右（或从右到左）访问每个节点。（第n层的所有节点都必须在第n+1层的节点之前访问）

//Breadth-first Search Traversal
template
     
     
      
      
void BST
      
      
       
       ::breadthFirst(){
  Queue
       
       
        
        
         
         *> queue;
  BSTNode
         
         
           *p = root; if(p!=0){ queue.enqueue(p); while(!queue.empty()){ p=queue.dequeue(); visit(p); if(p->left!=0) queue.enqueue(p->left); if(p->right!=0) queue.enqueue(p->right); } } }

0.3.4 深度优先遍历

深度优先遍历将尽可能地向左（或向右）发展，在遇到第一个转折点时，向右（或向左）一步，然后，再尽可能地向左（或向右）发展。

VLR-前序树遍历

LVR-中序树遍历

LRV-后序树遍历

template
     
     
      
      
void BST
      
      
       
       ::inorder(BSTNode
       
       
        
         *p){
  if(p!=0){
    inorder(p->left);
    visit(p);
    inorder(p->right);
  }
}

template
        
        
         
         
void BST
         
         
           ::preorder(BSTNode 
          
            *p){ if(p!=0){ visit(p); preorder(p->left); preorder(p->right); } } template 
           
             void BST 
            
              ::postorder(BSTNode 
             
               *p){ if(p!=0){ postorder(p->left); postorder(p->right); visit(p); } }

非递归版本

template
     
     
      
      
void BST
      
      
       
       ::iterativePreorder(){
  stack
       
       
        
        
         
         *> travStack;
  BSTNode
         
         
           *p = root; if(p!=0){ travStack.push(p); while(!travStack.empty()){ p = travStack.pop(); visit(p); if(p->right!=0) travStack.push(p->right); if(p->left!=0) //left child pushed after right travStack.push(p->left);//to be on the top of the stack; } } } template 
          
            void BST 
           
             ::iterativeInorder(){ stack 
             
             
               *> travStack; BSTNode 
              
                *p = root; while(p!=0){ while(p!=0){ //stack the right child(if any) if(p->right) // and the node itself when going to the left travStack.push(p->right); travStack.push(p); p = p->left; } p = travStack.pop(); //pop a node with no left child while(!travStack.empty() && p->right==0){ //visit it and al nodes with no right child; visit(p); p=travStack.pop(); } visit(p); // visit also the first node with a right child(if any) if(!travStack.empty()) p = travStack.pop(); else p = 0; } } void BST 
               
                 ::iterativePostorder(){ stack 
                 
                 
                   *> travStack; BSTNode 
                  
                    *p = root; *q=root; while(p!=0){ For(;p->left!=0;p=p->right) travStack.push(p); while(p!=0 && (p->right==0 ||p->right == q)){ visit(p); q = p; if(travStack.empty()) return; p = travStack.pop(); } travStack.push(p); p = p -> right; } }

0.4 森林的遍历

0.4.1．前序遍历

前序遍历的定义为：
(1) 访问森林中第一棵树的根结点；
(2) 前序遍历第一棵树的根结点的子树森林；
(3) 前序遍历剩余的其他子森林。

0.4.2．中序遍历

中序遍历的定义为：
(1) 中序遍历第一棵树的根结点的子树森林；
(2) 访问森林中第一棵的根结点；
(3) 中序遍历剩余的其他子森林。

0.5 树的存储结构

1．双亲(parents)链表表示法(from zh.Wikipedia.org)

/* 树节点的定义 */
#define MAX_TREE_SIZE 100
typedef struct
{
  TElemType data;
  int parent; /* 父节点位置域 */
} PTNode;
typedef struct
{
  PTNode nodes[MAX_TREE_SIZE];
  int n; /* 节点数 */
} PTree;

	H

	I

	J

	K

2．孩子(children)链表表示法(from zh.Wikipedia.org)

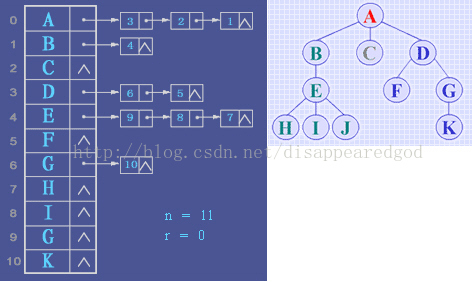
/*树的孩子链表存储表示*/
typedef struct CTNode { // 孩子节点
  int child;
  struct CTNode *next;
} *ChildPtr;
typedef struct {
  ElemType data； // 节点的数据元素
  ChildPtr firstchild； // 孩子链表头指针
} CTBox;
typedef struct {
  CTBox nodes[MAX_TREE_SIZE]；
  int n, r； // 节点数和根节点的位置
} CTree;

	H

	I

	J

	K

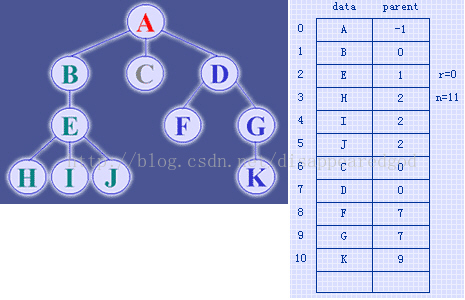
3．双亲孩子(parents-children)链表表示法

4．孩子兄弟(children-sibling)链表表示法

0.6 树、森林与二叉树的互相转换

0.6.1 树转换为二叉树

将一棵树转换为二叉树的方法是：
1．树中所有相邻兄弟之间加一条连线；
2．对树中的每个结点，只保留它与第一个儿子结点之间的连线，删去它与其它儿子结点之间的连线。
3．以树的根结点为轴心，将整棵树顺时针转动一定的角度，使之结构层次分明。

0.6.2 二叉树还原为树

树转换为二叉树这一转换过程是可逆的，可以依据二叉树的根结点有无右儿子结点，将一棵二叉树还原为树，具体方法如下：
1．若某结点是其双亲的左儿子，则把该结点的右儿子、右儿子的右儿子、…都与该结点的双亲结点用线连起来；
2．删掉原二叉树中所有的双亲结点与右儿子结点的连线；
3．整理由(1)、(2)两步所得到的树，使之结构层次分明。