回归分析

最新推荐文章于 2022-09-05 22:23:59 发布

yzlv

最新推荐文章于 2022-09-05 22:23:59 发布

阅读量3.6k

点赞数

分类专栏： R 数学建模文章标签：统计学 R语言

本文链接：https://blog.csdn.net/dmwithr/article/details/17080187

版权

数学建模同时被 2 个专栏收录

10 篇文章 0 订阅

订阅专栏

9 篇文章 1 订阅

订阅专栏

回归分析

1. 一元线性回归
2. (附录)一元线性回归的求解过程
3. 多元回归与逐步回归
4. 回归分析实现-R软件

1 一元线性回归

例

合金强度和碳含量

由专业知识知道, 合金的强度 y 与合金中碳的含量有关, 为了解他们之间的关系, 从生产中收集了一批数据, (xi,yi),i=1,⋯,n 具体数据如下

序号	碳含量x	强度	序号	碳含量x	强度y
1	0.10	42.0	7	0.16	49.0
2	0.11	43.5	8	0.17	53.0
3	0.12	45.0	9	0.18	50.0
4	0.13	45.5	10	0.20	55.0
5	0.14	45.0	11	0.21	55.0
6	0.15	47.5	12	0.23	60.0
…

数据读取与展示

thl<-read.table("data/thl.csv",sep=",",header=TRUE)
head(thl)

   thl   qd
1 0.10 42.0
2 0.11 43.5
3 0.12 45.0
4 0.13 45.5
5 0.14 45.0
6 0.15 47.5

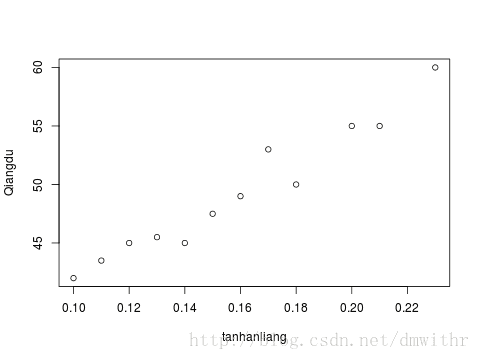
散点图展示数据

plot(thl,xlab="tanhanliang",ylab="Qiangdu")

一元回归分析模型
Y=β0+β1X+ε
- Y称为响应变量, X称为回归变量,
- β1 为回归系数, β0 称为截距, 统称为回归参数。
- 参数 β1 表示如果自变量 x增加一个单位, 则响应变量 Y 相应增加 β1 个单位。
样本数据

若 (xi,yi),i=1,⋯,n 为 (X,Y) 的一组观测值, 则一元线性回归模型可以表示为
$y i = β 0 + β 1 x i + ε i, i = 1, \dots, n$
其中误差相互独立, 并满足 E(εi)=0,var(εi)=σ2,i=1,⋯,n
回归参数的估计-最小二乘法

目标函数为(误差平方和)
$Q (β 0, β 1) = \sum i = 1 n (y i - β 0 - β 1 x i) 2$
使上述目标函数达到最小的 β0,β1 称为参数的最小二乘估计 β^0,β^1 ,即
$Q (β^0, β^1) = min β 0 β 1 Q (β 0, β 1)$
求解最小二乘问题

关于 β0,β1 分别求导, 并令之为0, 得方程组如下
$\partial \partial β 0 Q (β 0, β 1) \partial \partial β 1 Q (β 0, β 1) = - 2 \sum i = 1 n (y i - β 0 - β 1 x i) = 0 = - 2 \sum i = 1 n x i (y i - β 0 - β 1 x i) = 0$
上述方程组可以写作如下形式, 称为正规方程组
$- 2 \sum i = 1 n (1 x i) (y i - β 0 - β 1 x i) = (00)$
最小二乘法所得参数的估计
β^1=∑i=1n(xi−x¯)(yi−y¯)∑i=1n(xi−x¯)2=SxySxx,β^0=y¯−β^1x¯
- 其中
x¯=1n∑i=1nxi,y¯=1n∑i=1nyi,Sxx=∑i=1n(xi−x¯)2,Syy=∑i=1n(yi−y¯)2,Sxy=∑i=1n(xi−x¯)(yi−y¯)
上述诸变量的计算
- 在进行最小二乘法进行手动计算时，比较容易得出的是 $n, \sum i = 1 n x i, \sum i = 1 n y i, \sum i = 1 n x 2 i, \sum i = 1 n x i y i$
- 下面给出上述估计量的计算 $x ¯ S x x S x y = 1 n \sum i = 1 n x i, y ¯ = 1 n \sum i = 1 n \sum i = 1 n y i = \sum i = 1 n (x i - x ¯) (x i - x ¯) = \sum i = 1 n (x i - x ¯) x i - x ¯ \sum i = 1 n (x i - x ¯) = \sum i = 1 n x 2 i - n x ¯ 2 = \sum i = 1 n (x i - x ¯) (y i - y ¯) = \sum i = 1 n (x i - x ¯) y i = \sum i = 1 n x i y i - n x ¯ y ¯$
误差方差的估计
注意到 σ2 是未知的, 通过拟合之后的残差可以得出 σ2 的估计为

σ^2=1n−2∑i=1ne^2i

作为参数 σ2 的估计,
- 其中 e^i=yi−β^0−β^1xi 为残差
- 可以证明 σ^2 为 σ2 的无偏估计。
可以得出参数估计的均值和方差

$E (β^0) = β 0, E (β^1) = β 1$
说明估计量是无偏的,通过计算可得截距和斜率的估计的方差为
$V a r (β^0) = σ 2 (1 n + x ¯ 2 S x x), V a r (β^1) = σ 2 S x x$
参数估计量的分布

若给定误差服从正态分布, 可以得到
$β^1 \sim N (β 1, σ 2 S x x), 即 ( β ^ 1 - β 1 ) S x x - - - \sqrt σ 2 - - \sqrt \sim N (0, 1)$
另外有：
$( n - 2 ) σ ^ 2 σ 2 \sim χ 2 (n - 2)$
可以得出
$( β ^ 1 - β 1 ) S x x - - - \sqrt σ ^ 2 - - \sqrt \sim t (n - 2)$
根据这个分布可以进行回归方程的显著性检验
回归方程的显著性检验
- 从统计上讲, β1 是 E(Y) 随 X 线性变化的变化率, 若 β1=0 , 回归方程没有意义
- 回归方程的显著性检验需要检验如下假设： $H 0 : β 1 = 0, \leftrightarrow H 1 : β 1 \neq 0$
- 原假设成立时( β1=0 )可以采用t检验统计量对模型显著性进行检验 $t = β ^ 1 S x x - - - \sqrt σ ^\sim t (n - 2)$
  或 F 检验统计量
F=t2=β1^2Sxxσ^2∼F(1,n−2)
教材例子
1. 炼钢厂出钢时采用的盛钢水的钢包
  
  在使用过程中, 由于钢液及炉渣对包衬耐火材料的侵蚀, 使其容积不断增大, 希望找出使用次数与增大的容积之间的关系

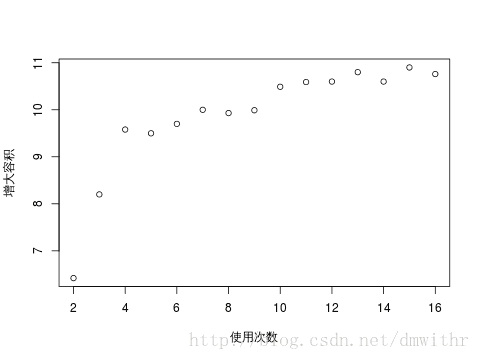
散点图

  x=c(2:16);
  y=c(6.42,8.20,9.58,9.50,9.70,10,9.93,9.99,10.49,10.59,10.6,10.8,10.6,10.9,10.76)
plot(x,y,xlab="使用次数",ylab="增大容积")

建模
根据数据特点, 首先进行非线性变换, 然后拟合如下模型

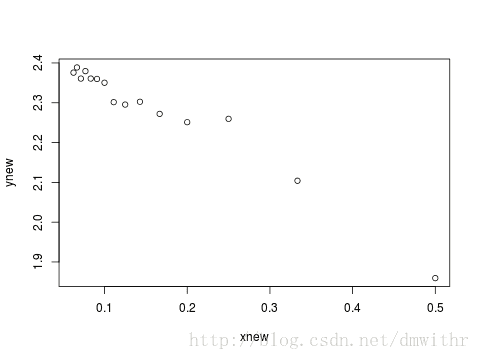
lnY=lna+bX

令 Y′=ln(Y),X′=X−1,β0=ln(a) , 则可以化为线性模型

Y′=β0+β1X′
```
ynew=log(y);xnew=1/x; plot(xnew,ynew)
```

线性回归过程

(l<-lm(ynew~xnew))

Call:
lm(formula = ynew ~ xnew)

Coefficients:
(Intercept)         xnew
       2.46        -1.11

线性回归详细结果

summary(l)

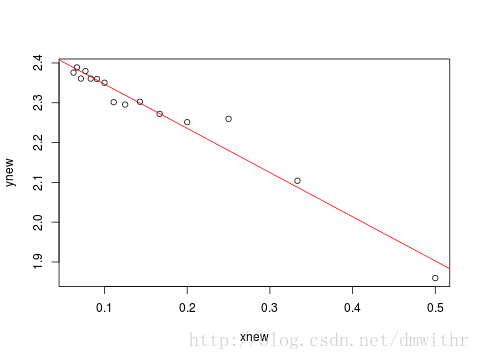
Call:
lm(formula = ynew ~ xnew)

Residuals:
     Min       1Q   Median       3Q      Max
-0.04303 -0.01506  0.00310  0.00611  0.07956

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)   2.4578     0.0126   195.2  < 2e-16 ***
xnew         -1.1107     0.0638   -17.4  2.2e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.029 on 13 degrees of freedom
Multiple R-squared: 0.959,	Adjusted R-squared: 0.956
F-statistic:  303 on 1 and 13 DF,  p-value: 2.17e-10

拟合后的图形
```
plot(xnew,ynew)
abline(l,col=2)
```

matlab 实现上述过程

x=[2:16]';
y=[6.42;8.20;9.58;9.50;9.70;10;9.93;9.99;
   10.49;10.59;10.6;10.8;10.6;10.9;10.76];
ynew=log(y);xnew=[ones(15,1),1./x];
[b,bint,~,~,stats]=regress(ynew,xnew)

b =
2.4578
-1.1107
bint =
2.4306    2.4850
-1.2485   -0.9729
stats =
0.9589  303.1896    0.0000    0.0008

2 (附录)一元线性回归的求解过程

回归参数的最小二乘法估计

目标函数为(误差平方和)
$Q (β 0, β 1) = \sum i = 1 n (y i - β 0 - β 1 x i) 2$
关于 β0,β1 分别求导, 并令之为0, 得方程组如下
$\partial \partial β 0 Q (β 0, β 1) \partial \partial β 1 Q (β 0, β 1) = - 2 \sum i = 1 n (y i - β 0 - β 1 x i) = 0 = - 2 \sum i = 1 n x i (y i - β 0 - β 1 x i) = 0$
上述方程组可以写作如下形式, 称为正规方程组
$- 2 \sum i = 1 n (1 x i) (y i - β 0 - β 1 x i) = (00)$
正规方程组解的存在性

将上述方程组进行化简
$⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ n β 0 + (\sum i = 1 n x i) β 1 = \sum i = 1 n y i, (\sum i = 1 n x i) β 0 + (\sum i = 1 n x 2 i) β 1 = \sum i = 1 n x i y i$
称为正规方程组, 由于 xi 不完全相同, 其系数行列式
$∣ ∣ ∣ ∣ ∣ ∣ ∣ n \sum i = 1 n x i \sum i = 1 n x i \sum i = 1 n x 2 i ∣ ∣ ∣ ∣ ∣ ∣ ∣ = n \sum i = 1 n (x i - x) 2 \neq 0$
上述方程有唯一解
正规方程组

$- 2 \sum i = 1 n (1 x i) (y i - β 0 - β 1 x i) = (00)$
将上述方程展开，写作
$- 2 ⎛ ⎝ ⎜ ⎜ ⎜ 11 ⋮ 1 x 1 x 2 ⋮ x n ⎞ ⎠ ⎟ ⎟ ⎟ T ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ y 1 - β 0 - β 1 x 1 y 2 - β 0 - β 1 x 2 ⋮ y n - β 0 - β 1 x n ⎞ ⎠ ⎟ ⎟ ⎟ ⎟ = (0 0)$
方程组的矩阵表示:
- 记 $Y = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ y 1 y 2 ⋮ y n ⎞ ⎠ ⎟ ⎟ ⎟ ⎟, X = ⎛ ⎝ ⎜ ⎜ ⎜ 11 ⋮ 1 x 1 x 2 ⋮ x n ⎞ ⎠ ⎟ ⎟ ⎟, β = (β 0 β 1)$
- 则上述方程可以简化为 $- 2 X T (Y - X β) = 0$
方程组的另一种解释(向量求导数)

$Q (β) = Q (β 0, β 1) = (Y - X β) T (Y - X β)$
则关于 β 求偏导数, 令之为零, 有
$\partial \partial β Q (β) = - 2 X T (Y - X β) = 0$
求解
$X T X β = X T Y$
回归参数的最小二乘估计

解之可得：
$β^= (X T X) - 1 X T Y = ⎛ ⎝ ⎜ n n x ¯ n x ¯ \sum i = 1 n x 2 i ⎞ ⎠ ⎟ - 1 ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ \sum i = 1 n y i \sum i = 1 n x i y i ⎞ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟$
回归参数估计的性质

注意到
$β^= (X T X) - 1 X T Y, Y = X β + ε$
有
$β^= β + (X T X) - 1 X T ε$
由此可得估计量的均值和方差为
$E (β^) = β, V a r (β^) = σ 2 (X T X) - 1$
截距和斜率估计的方差

注意到：
$(X T X) - 1 = ⎛ ⎝ ⎜ n n x ¯ n x ¯ \sum i = 1 n x 2 i ⎞ ⎠ ⎟ - 1 = ⎛ ⎝ ⎜ ⎜ ⎜ 1 n + x ¯ 2 S x x x ¯ S x x x ¯ S x x 1 \sum ( x i - x ¯ ) 2 ⎞ ⎠ ⎟ ⎟ ⎟$
可得 β^0,β^1 的方差分别为
$V a r (β^0) = σ 2 (1 n + x ¯ 2 S x x), V a r (β^1) = σ 2 S x x$

3 多元回归与逐步回归

多元回归分析的数学模型

设自变量为 x1,x2,⋯,xp 目标变量为 Y , 满足
$y = β 0 + β 1 x 1 + \dots + β p x p + ε$
设从上述模型得到 n 个相互独立的观测，即有
$⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ y 1 = β 0 + β 1 x 11 + β 2 x 12 + \dots + β p x 1 p + ε 1 y 2 = β 0 + β 1 x 21 + β 2 x 22 + \dots + β p x 2 p + ε 2 \dots \dots \dots \dots y n = β 0 + β 1 x n 1 + β 2 x n 2 + \dots + β p x n p + ε n$
其中 , ε1,ε2,⋯,εn 为测量误差, 相互独立, 服从正态分布 N(0,σ2) . σ2 为未知方差.
模型的矩阵表示

$y = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ y 1 y 2 ⋮ y n ⎞ ⎠ ⎟ ⎟ ⎟ ⎟, X = ⎛ ⎝ ⎜ ⎜ ⎜ 1111 x 11, x 12, \dots, x 1 p x 21, x 22, \dots, x 2 p \dots, \dots, \dots, \dots x n 1, x n 2, \dots, x n p ⎞ ⎠ ⎟ ⎟ ⎟, β = ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ β 0 β 1 ⋮ β p ⎞ ⎠ ⎟ ⎟ ⎟ ⎟, ε = ⎛ ⎝ ⎜ ⎜ ⎜ ε 1 ε 2 ⋮ ε n ⎞ ⎠ ⎟ ⎟ ⎟$
模型重新表述为
$Y = X β + ε$
上述方程称为线性回归方程的数学模型。
正规方程组

利用最小二乘法(或极大似然估计), 取
$Q (β) = (Y - X β) T (Y - X β)$
由方程组
$\partial \partial β Q (β) = 0$
可以得到
$- 2 X T (Y - X β) = 0 \Rightarrow X T X β = X T Y$
线性回归系数 β 的估计

令 A=XTX 为 p+1 可逆方阵, 则由模型可得
$β^= A - 1 X T Y$
注意到 Y=Xβ+ε ,从而有 β^=β+A−1XTε ,可以得到
$E (β^) = β, C o v (β^) = σ 2 A - 1, v a r (β^j) = σ 2 C j + 1, j + 1$
其中 Cjj 为矩阵 A−1 第 j 个主对角元的值
关于最小二乘估计的注记(new)
- Y 的预测值 Y^=XTβ^ 是向量 Y 在X的列空间的投影只需要证明 XT(Y−Y^)=0 即可, 说明 X 的列向量和拟合之后的残差是正交的 $Y^= Y - Y^= X T (Y - Y^) = = X β^= X (X T X) - 1 X T Y (I - X (X T X) - 1 X T) Y X T (I - X (X T X) - 1 X T) Y (X T - X T X (X T X) - 1 X T) Y = (X - X) T Y = 0$
说明估计值 Y^=XTβ^ 是 Y 到 X 的列向量空间上的投影
误差方差的估计

记
$残差平方和 S S E = \sum i = 1 n (y i - y^i) 2 回归平方和 S S R = \sum i = 1 n (y^i - y ¯) 2 总平方和 S S T = \sum i = 1 n (y i - y ¯) 2$
则有
$S S T = S S E + S S R$
采用
$σ^2 = 1 n - p - 1 S S E = 1 n - p - 1 \sum i = 1 n (y i - y^i) 2$
作为模型误差方差的估计, 可以证明这个估计是无偏的
$E (σ^2) = σ 2$
模型的分析与检验用到的相关结论

记 y¯=1n∑i=1nyi
$S S R σ 2 \sim χ 2 (p), S S E σ 2 \sim χ 2 (n - p - 1),$
且相互独立, 得模型检验统计量
$F = S S R / p S S E / ( n - p - 1 ) \sim F (p, n - p - 1)$
假设检验
原假设H0:β1=β2=⋯=βp=0↔备择假设H1:至少有一个不为零

检验标准为: 当p-value小于给定的小概率值时, 拒绝原假设 H0
- 当 H0 被拒绝, 说明方程中的系数不全为0, 方程是有效的
- 若 H0 被接受, 则说明方程无效, 变量 x1,x2,⋯,xp 对目标变量无线性关系, 此时需要从其他角度考虑该系统
回归方程系数的显著性检验

对假设 Hj0:βj=0↔备择假设Hj1:βj≠0 可以证明 σ 已知时
$β ^ j - 0 c j j - - \sqrt σ \sim N (0, 1)$
从而在 σ 未知时, 采用如下检验统计量
$t j = β ^ j c j + 1 , j + 1 S S E / ( n - p - 1 ) - - - - - - - - - - - - - - - - - - - \sqrt \sim t (n - p - 1)$
其中 cj,j 是 A−1=(XTX)−1 的主对角元上第 j 个元素
检验方法
- 当 pi 小于给定的小概率值时, 拒绝原假设
- 若对于某个 j0 ,假设 βj0=0 被接受, 则第 j0 个变量应从方程中剔除
- 这是选择有显著作用变量的方法
回归方程进行预测预报和控制

经过回归分析得到经验回归方程为
$y = β^0 + β^1 x 1 + \dots + β^p x p$
设要在某已知点进行预测, 可得到点估计
$y^0 = β^0 + β^1 x 01 + \dots + β^p x 0 p$
预测值的置信区间
- 设真实的值为 y , 则有 $y^0 - y \sim N (0, b 2 σ 2)$
  其中
  $b 2 = 1 + 1 n + \sum i = 1 p \sum j = 1 p C i j (x 0 i - x ¯ i) (x 0 j - x ¯ j)$
- 用 σ 的估计 SSEn−p−1−−−−−√ 代替 σ 有可得 $y - y ^ 0 S S E / ( n - p - 1 ) - - - - - - - - - - - - - \sqrt \sim t (n - p - 1)$
- 得 y 的预测区间为 $⎡ ⎣ y^0 \pm t α 2 (n - p - 1) S S E n - p - 1 - - - - - - - - \sqrt ⎤ ⎦$
最优逐步回归分析
在线性回归中, 经过模型检验, 发现线性方程作用显著, 同时有一些变量可以剔除, 这里介绍一种最优逐步回归方法, 其基本思想为：
1. 首先对每个因子 xi 进行逐个检验, 确认其在方程中的作用显著程度
2. 然后依显著程度从大到小引入变量到方程, 并及时进行检验, 去掉作用不显著的变量
3. 依次循环, 到最后无因子进入方程, 同时也没有因子从方程中剔除
回归变量的选择的标准
回归变量的选择问题的最大困难在于如何比较不同子集选择的优劣, 即最优选择的标准问题。
- 均方误差 s2 最小: s2(A)=ESS(A)/(n−l−1) 达到最小, 其中 ESS(A) 是Y与子集 A回归模型的误差平方和, l 是子集A中自变量的个数
- 预测均方误差最小: 选择子集A 使得 J(A)=n+l+1n−l−1ESS(A) 达到最小
- Cp 统计量最小准则 : Cp(A)=ESS(A)ESS(A)/(n−l−1)+2l−n
- AIC或 BIC准则:选择子集A, 使得 AIC(A)=ln(ESS(A))+2ln 或 BIC(A)=ln(ESS(A))+llnnn 达到最小
- 修正 R2 准则:选择子集A,使得 R2=1−n−in−l(1−R2) (当模型包含截距时, i=1,否则 i=0)达到最大
常见统计软件中的最优子集回归方法
- 逐步筛选法(stepwise),向前引入法(Forward) ,向后剔除法 (Backward)
- 计算量最大的全子集法, 计算所有可能的子集, 并按最优选择标准选择最优的回归方程, 包括 R2 (RSQUARE)选择法, Cp 统计量选择法 , 修正 R2 (ADJRSQ)选择法
- 计算量适中的选择法：最小 R2 增量法和最大 R2 增量法

4 回归分析实现-R软件

模拟数据

模型为：
$y = 1 + x 1 + 2 x 2 + 3 x 3 + ε$
产生100条数据, 进行回归拟合

程序代码

n<-100
set.seed(1314)
x<-matrix(runif(4*n,-1,1),ncol=4)
e<-rnorm(n)
beta<-c(1,2,3,0)
y<-1+x%*%beta+e
l1<-lm(y~x)
summary(l1)

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max
-2.3195 -0.7293  0.0027  0.7208  2.6831

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)    0.976      0.103    9.43  2.7e-15 ***
x1             1.100      0.172    6.40  6.0e-09 ***
x2             2.010      0.190   10.60  < 2e-16 ***
x3             2.766      0.183   15.08  < 2e-16 ***
x4            -0.151      0.189   -0.80     0.43
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.02 on 95 degrees of freedom
Multiple R-squared: 0.803,	Adjusted R-squared: 0.795
F-statistic: 96.9 on 4 and 95 DF,  p-value: <2e-16

模拟结果

Call: lm(formula = y ~ x)
Residuals:
    Min      1Q  Median      3Q     Max
-3.2558 -0.6263  0.0412  0.6247  2.3635
Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  0.93393    0.10641   8.777 6.79e-14 ***
x1           0.94337    0.18801   5.018 2.43e-06 ***
x2           1.98444    0.17508  11.335  < 2e-16 ***
x3           3.26633    0.17634  18.523  < 2e-16 ***
x4          -0.02989    0.18236  -0.164     0.87
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.049 on 95 degrees of freedom
Multiple R-squared: 0.8376,	Adjusted R-squared: 0.8308
F-statistic: 122.5 on 4 and 95 DF,  p-value: < 2.2e-16

实例分析

回归模型估计的主要任务
y=β0+β1x1+⋯+βpxp+ε,ε∼N(0,σ2)
- 通常我们需要估计其中的参数 β0,β1,⋯,βp 和 σ2 并初步判定其中的系数参数 (除 β0 外）是否为０

例－－年薪与相关因素分析

工薪阶层普遍关心年薪与哪些因素有关, 由此可以制定自己的奋斗目标, 某机构希望估计从业人员的年薪(万元）与他们的成果（论文, 著作等）的质量指标 X1 , 从事本工作的时间 X2 （年）, 能承购获得资助的指标 X3 之间的关系, 为此调查了24位从业人员, 的数据如下

i	1	2	3	4	5	6
Xi1	3.5	5.3	5.1	5.8	4.2	6.0	…
Xi2	9	20	18	33	31	13	…
Xi3	6.1	6.4	7.4	6.7	7.5	5.9	…
yi	11.1	13.4	12.9	15.6	13.8	12.5	…

数据输入

将需要输入的数据做成如下类型的文本文件, 存为后缀为csv的数据文件
data/nianxin.csv
读取数据，观察数据结构

## 年薪数据
g<-read.table('data/nianxin.csv',header=TRUE,sep=",")
head(g)

   x1 x2  x3    y
1 3.5  9 6.1 11.1
2 5.3 20 6.4 13.4
3 5.1 18 7.4 12.9
4 5.8 33 6.7 15.6
5 4.2 31 7.5 13.8
6 6.0 13 5.9 12.5

问题求解
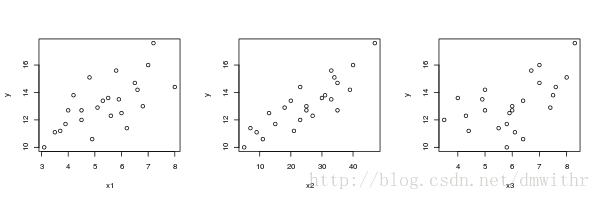
- 导入数据分别作出 y 关于三个自变量的散点图, 观察数据之间的关系
```
par(mfrow=c(1,3))
plot(g[,c(1,4)])
plot(g[,c(2,4)])
plot(g[,3:4])
par(mfrow=c(1,1))
```

实现回归的R代码和回归结果

nianxin.lm<-lm(y~.,data=g)
summary(nianxin.lm)

Call:
lm(formula = y ~ ., data = g)

Residuals:
    Min      1Q  Median      3Q     Max
-1.0547 -0.2851  0.0348  0.3263  1.1056

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)   5.8695     0.6657    8.82  2.5e-08 ***
x1            0.3689     0.1069    3.45  0.00253 **
x2            0.1080     0.0121    8.94  2.0e-08 ***
x3            0.4358     0.0975    4.47  0.00024 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.572 on 20 degrees of freedom
Multiple R-squared: 0.914,	Adjusted R-squared: 0.901
F-statistic:   71 on 3 and 20 DF,  p-value: 7.67e-11

Validate

yzlv

关注

0
点赞
踩
10

收藏

觉得还不错? 一键收藏
2
评论
回归分析

1 一元线性回归例合金强度和碳含量由专业知识知道, 合金的强度 y 与合金中碳的含量有关, 为了解他们之间的关系, 从生产中收集了一批数据, (xi,yi),i=1,⋯,n 具体数据如下序号碳含量x强度序号碳含量x强度y10.1042.070.16
复制链接

扫一扫