Leetcode: Sqrt(x)_sqrt(x) leetcode java-CSDN博客

该博客主要介绍了如何在LeetCode上解决求解整数平方根的问题。首先，作者提到可以采用二分查找的方法来解决，但需要注意类型溢出问题，可能需要使用更大的数据类型。其次，文章详细解释了牛顿迭代法的原理，通过不断逼近求解f(x)=x^2-n的根，给出迭代公式并展示了如何将该方法应用于实现sqrt(x)的计算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Implement int sqrt(int x).

Compute and return the square root of x.

1. 二分法：

这道题一看到函数的定义int sqrt(int x)都是int就高兴了，直接二分吧。但是要注意，即使用long long都TM越界，还要用unsigned long long。最后返回值还要再检查一下。

int sqrt(int x) {
        // Start typing your C/C++ solution below
        // DO NOT write int main() function
        unsigned long long begin = 0;
        unsigned long long end = (x+1)/2;
        unsigned long long mid;
        unsigned long long tmp;
        while(begin < end)
        {
            mid = begin + (end-begin)/2;
            tmp = mid*mid;
            if(tmp==x)return mid;
            else if(tmp<x) begin = mid+1;
            else end = mid-1;
        }
        tmp = end*end;
        if(tmp > x)
            return end-1;
        else
            return end;
    }

2. 牛顿迭代法

为了方便理解，就先以本题为例：

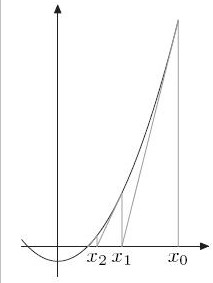
计算x² = n的解，令f(x)=x²-n，相当于求解f(x)=0的解，如左图所示。

首先取x₀，如果x₀不是解，做一个经过(x₀,f(x₀))这个点的切线，与x轴的交点为x₁。

同样的道理，如果x₁不是解，做一个经过(x₁,f(x₁))这个点的切线，与x轴的交点为x₂。

以此类推。

以这样的方式得到的x_i会无限趋近于f(x)=0的解。

判断x_i是否是f(x)=0的解有两种方法：

一是直接计算f(x_i)的值判断是否为0，二是判断前后两个解x_i和x_i-1是否无限接近。

经过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f'(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f'(x_i)。

继续化简，x_i+1=x_i - (x_i²- n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2。

有了迭代公式x_i+1= (x_i + n/x_i) / 2，程序就好写了。关于牛顿迭代法，可以参考wikipedia以及百度百科。

int sqrt(int x) {
		// Start typing your C/C++ solution below
        // DO NOT write int main() function
        if (x ==0)
            return 0;
        double pre;
        double cur = 1;
        do
        {
            pre = cur;
            cur = x / (2 * pre) + pre / 2.0;
        } while (abs(cur - pre) > 0.00001);
        return int(cur);
    }

float InvSqrt(float x)
{
    float xhalf = 0.5f*x;
    int i = *(int*)&x; // get bits for floating VALUE
    i = 0x5f375a86- (i>>1); // gives initial guess y0
    x = *(float*)&i; // convert bits BACK to float
    x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
    return x;
}