Link-Cut-Tree
概念
LCT大约是树链剖分和Splay的结合版,因为要动态维护树的结构和树上的信息,所以把维护重边的线段树换成更灵活的Splay。Splay作为辅助树是按深度来维护树上的一条链,就像是维护树上的一个序列一样。
主要操作围绕access和splay来进行。
模板
1.Access
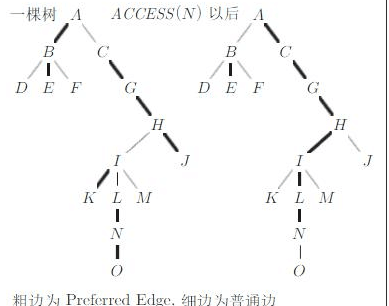
Access(x)操作就是把x到根的路径上的点的path father全部设为路径上的点且每个点的preferred son都设为路径上的点.这么说有点绕,还是上张图比较好。
void access(int x)
{
splay(x);
t[t[x].ch[1]].pf=x;t[t[x].ch[1]].fa=0;
t[x].ch[1]=0;
while(t[x].pf!=0)
{
int u=t[x].pf;
splay(u);
t[x].pf=0;
t[t[u].ch[1]].pf=u;t[t[u].ch[1]].fa=0;
t[u].ch[1]=x;t[x].fa=u;
update(u);
x=u;
}
}2.findroot
这个应该比较简单,直接access,splay然后向左一路找下去即可
int findroot(int x)
{
access(x);
splay(x);
while(t[x].ch[0])x=t[x].ch[0];
return x;
}3.beroot
这个应该也比较简单,只需access(x)然后splay(x)最后打上翻转标记。
void beroot(int x)
{
access(x);
splay(x);
t[x].rev^=1;
}4.link
先保证root不相等
然后access(y),beroot(x)
把x的pf设为y
void link(int x,int y)
{
beroot(x);
access(y);
t[x].pf=y;
}5.cut
先让x成为根,然后access(y),splay(y),这时y的左节点只有x,然后断去即可。
void cut(int x,int y)
{
beroot(x);
access(y);
splay(y);
t[y].ch[0]=0;
t[x].fa=t[x].pf=0;
update(y);
}























 1177
1177

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








