木块砌墙算法(C#版)
首先感谢 网友“⒌1→⑤Ⅵ℡” 提供算法讲解和其他网友提供的帮助。
原题链接:http://hero.pongo.cn/Question/Details?ID=36&ExamID=36
简化图形:因为厚度始终是1,所以这个墙可以简化成平面的图形。即 2^N * K 的图形。
刚看到这个题,第一想到的就是遍历法,也想不出更好的办法。但是这个问题的规模很大,用遍历只能求规模很小的情况,当规模变大时,基本上不能用该算法进行求解。但是为了更快的看到结果,我还是实现了这个算法,这样可能有助于新算法的编写,至少可以知道规模较小情况下的结果,用于验证新算法是否正确。
本文使用的图示说明:
一、遍历方法求解
我的遍历思路是:用二维数组模拟墙,从左下角开始摆放,从左往右,从下往上,最后一个格子是右上角那个位置;每个格子把每种可以摆放木块都摆放一次,每堆满一次算一种用摆放方法。下面图示演示算法过程(n=1,k=2)
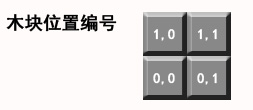
下面是我的遍历算法的演示过程。
此方法优点,可以输出每种堆放方法。
因为这种算法只是过渡算法,所以这里不做详细解释。如有不理解的,请留言。下面给出上面算法的代码:
using System;
using System.Collections.Generic;
using System.Text;
namespace HeapBlock
{
public delegate void OnFindWallDelegate(int[,] wall);
public class Wall
{
private int width;
private int height;
private int[,] wall;
private int x;
private int y;
private int result = 0;
public Wall(int width, int height)
{
this.x = 0;
this.y = 0;
this.width = width;
this.height = height;
this.wall = new int[height, width];
}
public event OnFindWallDelegate OnFindWall;
public int GetResult()
{
return result;
}
public void HeapBlock()
{
if (IsFull())
{
result++;
if (OnFindWall != null)
{
OnFindWall(wall);
}
return;
}
if (CellNotUsed())
{
if (CanBeSetBlock(1))
{
this.SetBlock(1);
this.NextCell();
HeapBlock();
this.PrevCell();
this.ClearBlock(1);
}
if (CanBeSetBlock(2))
{
this.SetBlock(2);
this.NextCell();
HeapBlock();
this.PrevCell();
this.ClearBlock(2);
}
if (CanBeSetBlock(3))
{
this.SetBlock(3);
this.NextCell();
HeapBlock();
this.PrevCell();
this.ClearBlock(3);
}
}
else
{
this.NextCell();
HeapBlock();
this.PrevCell();
return;
}
}
private void SetBlock(int blockType)
{
if (blockType == 1)
{
wall[y,x] = blockType;
}
else if (blockType == 2)
{
wall[y,x] = blockType;
wall[y,x + 1] = -1;
}
else if (blockType == 3)
{
wall[y,x] = blockType;
wall[y + 1,x] = -1;
}
}
private void ClearBlock(int blockType)
{
if (blockType == 1)
{
wall[y,x] = 0;
}
else if (blockType == 2)
{
wall[y,x] = 0;
wall[y,x + 1] = 0;
}
else if (blockType == 3)
{
wall[y,x] = 0;
wall[y + 1,x] = 0;
}
}
private bool CanBeSetBlock(int blockType)
{
if (!InWallArea() && !CellNotUsed())
{
return false;
}
if (blockType == 1)
{
return true;
}
else if (blockType == 2)
{
return InWallArea(x + 1, y) && CellNotUsed(x + 1, y);
}
else if (blockType == 3)
{
return InWallArea(x, y + 1) && CellNotUsed(x, y + 1);
}
else
{
return false;
}
}
private bool CellNotUsed(int x, int y)
{
return wall[y,x] == 0;
}
private bool CellNotUsed()
{
return CellNotUsed(x, y);
}
private bool InWallArea(int x, int y)
{
return (0 <= x && x < width) && (0 <= y && y < height);
}
private bool InWallArea()
{
return InWallArea(x, y);
}
private void NextCell()
{
x = x < width - 1 ? x + 1 : 0;
y = x == 0 ? y + 1 : y;
}
private void PrevCell()
{
x = x == 0 ? width - 1 : x - 1;
y = x == width - 1 ? y - 1 : y;
}
private bool IsFull()
{
return x >= width || y >= height;
}
}
}
Wall类使用方法:
Wall wal = new Wall(width, height);
//wal.OnFindWall += new OnFindWallDelegate(wal_OnFindWall); //可以注册事件。没找到一种堆放方法,就触发该事件。
wal.HeapBlock(); //开始堆放木墙
Console.Write(wal.GetResult()); //输出结果。
二、问题分解方法(递归)
问题分解就是把一个大问题,分解成小问题,逐个求解,然后再解决大问题。
首先说明“?方块”的作用
这个块表示右上角位置被半块绿色木块占用,其他位置空闲。
“?方块”,表示这个位置是空位置,可以任意摆放。
上图的意思就是,当右上角被绿色木块占用,此位置固定不变,其他位置任意摆放,在这种情况下的堆放方案数。
假如有墙规模为(n,k),如果从中间切开,被分为规模问(n-1,k)的两堵墙。那么被分开的墙和原墙有什么关系呢?我们首先来看一下几组演示。
首先演示,n=1,k=2时的算法演算
图 2-1
图示说明:

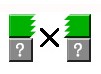
这个是排列组合的知识。
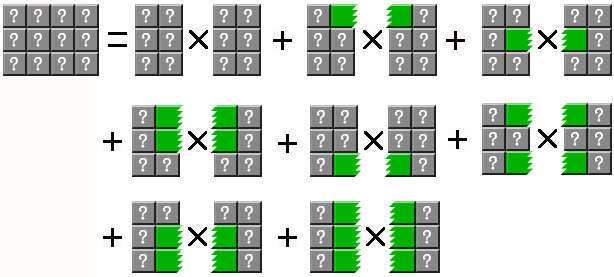
再演示一组更具一般性的计算分解。当n=2,k=3的情况。
图 2-2
再从分解的结果中,挑选一组进行分解演示:
图 2-3
通过图2-2和图2-3的分解演示,可以说明,最终都是分解成一列求解。在逐级向上汇总。
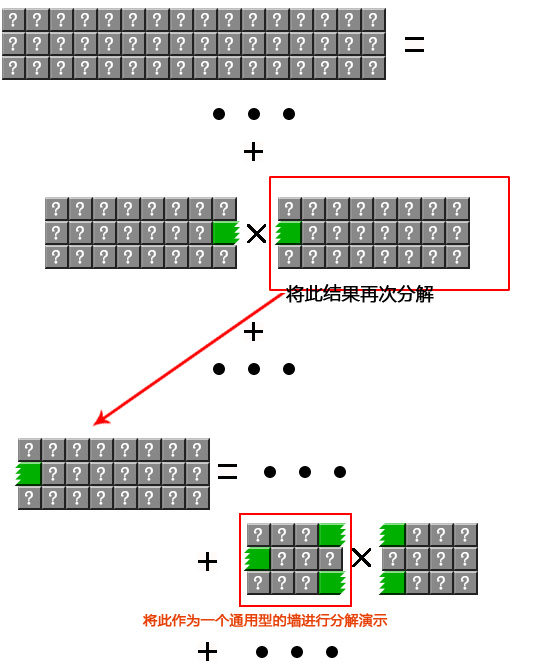
我们再假设一堵墙n=4,k=3。也就是说,宽度是16,高度是3。会有以下分解。
图2-4
根据上面的分解的一个中间结果,再进行分解,如下:
图 2-5
通过上面的演示可以明确一点,假设f(n)用于计算问题,那么f(n)依赖于f(n-1)的多种情况。我们再来看看,切开处的有什么特殊的地方。
通过对上面图示分解演示过程,可以知道,被切开的两堵墙从没有互相嵌入的木块(绿色木块)到全是互相连接的木块。切口绿色木块的全排列,有2^k种状,比如k=2,就有00、01、10、11,4中状态。根据排列组合的性质,把每一种状态下左右木墙堆放方案数相乘,再把所有乘积求和,就得到木墙的堆放结果数。以此类推,将问题逐步往下分解。从图2-5中可以看出,除了需要考虑切口绿色木块的状态,还需要考虑最左边一列和最右边一列的绿色木块状态。我们把这两种边界状态称为左边界状态和右边界状态,分别用leftState和rightState表示。
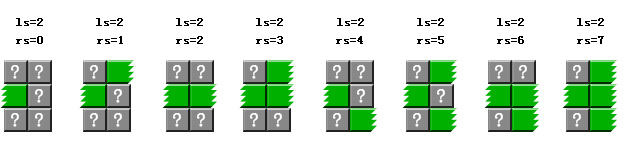
观察图2-5被切分后,所有左边的墙,他们的左边界状态始终保持不变,右边界状态从0~maxState, maxState = 2^k-1(有绿色方块表示1,没有表示0;ls表示左边界状态,rs表示右边状态):
图 2-6
同样可以看出右边的墙的右边界状态保持不变,而左边界状态从0~maxState。
要堆砌的木墙可以看做是左边界状态=0,和右边界状态=0的一堵墙。
根据图示分解过程可以得到以下方程
函数返回结果,就是,当左边状态为=leftState,右边状态=rightState时,木墙的堆砌方案数。本题要求解的就是左右状态都为0的情况。
如,n=1024,k=4,进行如下调用即可:f(1024,4,0,0)
用方程来表示图形:

这个用方程表示为 f(2,3,2,5)
来看看方程是如何表示图形的分解。
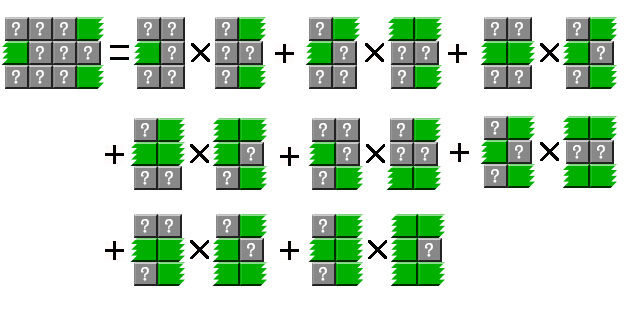
比如,图2-2 的方程式表示为:
f(2,3,0,0) = f(1,3,0,0)*f(1,3,0,0) + f(1,3,0,1)*f(1,3,1,0) + f(1,3,0,2)*f(1,3,2,0)
+ f(1,3,0,3)*f(1,3,3,0) + f(1,3,0,4)*f(1,3,4,0) + f(1,3,0,5)*f(1,3,5,0)
+ f(1,3,0,6)*f(1,3,6,0) + f(1,3,0,7)*f(1,3,7,0)
当n=0,表示墙就一列,此时不能再分解。直接计算结果进行返回。
当n=1,墙两列,分解时有些状态可能不能使用,需要排除。如图2-3
下面代码就是根据上面函数原理编写的。最终执行效率,n=1024,k=4 时,用时0.2800160秒。
源代码使用过了字典作为缓存,用时在1.3秒左右。后来改为数组结果,性能大增。
using System;
using System.Collections.Generic;
using System.Text;
using System.Collections;
namespace HeapBlock
{
public class WoolWall
{
private int n;
private int height;
private int maxState;
private int[, ,] resultCache; //结果缓存数组
public WoolWall(int n, int height)
{
this.n = n;
this.height = height;
maxState = (1 << height) - 1;
resultCache = new int[n + 1, maxState + 1, maxState + 1]; //构建缓存数组,每个值默认为0;
}
/// <summary>
/// 静态入口。计算堆放方案数。
/// </summary>
/// <param name="n"></param>
/// <param name="k"></param>
/// <returns></returns>
public static int Heap(int n, int k)
{
return new WoolWall(n, k).Heap();
}
/// <summary>
/// 计算堆放方案数。
/// </summary>
/// <returns></returns>
public int Heap()
{
return (int)Heap(n, 0, 0);
}
private long Heap(int n, int lState, int rState)
{
//如果缓存数组中的值不为0,则表示该结果已经存在缓存中。
//直接返回缓存结果。
if (resultCache[n, lState, rState] != 0)
{
return resultCache[n, lState, rState];
}
//在只有一列的情况,无法再进行切分
//根据列状态计算一列的堆放方案
if (n == 0)
{
return CalcOneColumnHeapCount(lState);
}
long result = 0;
for (int state = 0; state <= maxState; state++)
{
if (n == 1)
{
//在只有两列的情况,判断当前状态在切分之后是否有效
if (!StateIsAvailable(n, lState, rState, state))
{
continue;
}
result += Heap(n - 1, state | lState, state | lState) //合并状态。因为只有一列,所以lState和rState相同。
* Heap(n - 1, state | rState, state | rState);
}
else
{
result += Heap(n - 1, lState, state) * Heap(n - 1, state, rState);
}
result %= 1000000007;//为了防止结果溢出,根据题目要求求模。
}
resultCache[n, lState, rState] = (int)result; //将结果写入缓存数组中
resultCache[n, rState, lState] = (int)result; //对称的墙结果相同,所以直接写入缓存。
return result;
}
/// <summary>
/// 根据一列的状态,计算列的堆放方案数。
/// </summary>
/// <param name="state">状态</param>
/// <returns></returns>
private int CalcOneColumnHeapCount(int state)
{
int sn = 0; //连续计数
int result = 1;
for (int i = 0; i < height; i++)
{
if ((state & 1) == 0)
{
sn++;
}
else
{
if (sn > 0)
{
result *= CalcAllState(sn);
}
sn = 0;
}
state >>= 1;
}
if (sn > 0)
{
result *= CalcAllState(sn);
}
return result;
}
/// <summary>
/// 类似于斐波那契序列。
/// f(1)=1
/// f(2)=2
/// f(n) = f(n-1)*f(n-2);
/// 只是初始值不同。
/// </summary>
/// <param name="k"></param>
/// <returns></returns>
private static int CalcAllState(int k)
{
return k <= 2 ? k : CalcAllState(k - 1) + CalcAllState(k - 2);
}
/// <summary>
/// 判断状态是否可用。
/// 当n=1时,分割之后,左墙和右边墙只有一列。
/// 所以state的状态码可能会覆盖原来的边缘状态。
/// 如果有覆盖,则该状态不可用;没有覆盖则可用。
/// 当n>1时,不存在这种情况,都返回状态可用。
/// </summary>
/// <param name="n"></param>
/// <param name="lState">左边界状态</param>
/// <param name="rState">右边界状态</param>
/// <param name="state">切开位置的当前状态</param>
/// <returns>状态有效返回 true,状态不可用返回 false</returns>
private bool StateIsAvailable(int n, int lState, int rState, int state)
{
return (n > 1) || ((lState | state) == lState + state && (rState | state) == rState + state);
}
}
}
代码分析
1,如何使用
WoolWall.Heap(1024,4); //直接通过静态方法获得结果。
new WoolWall(n, k).Heap();//通过构造对象获得结果。
2,缓存
因为他最终都是分解成一列的情况进行处理,这就会导致很慢。为了提高速度,本文使用了缓存机制来提高性能。缓存原理就是,n,k,leftState,rightState相同的墙,返回的结果肯定相同。利用这个特性,每计算一种结果就放入到缓存中,如果下次计算直接从缓存取出。刚开始缓存用字典类实现,有网友给出了更好的缓存方法——数组。这样性能好了很多,也更加简单。
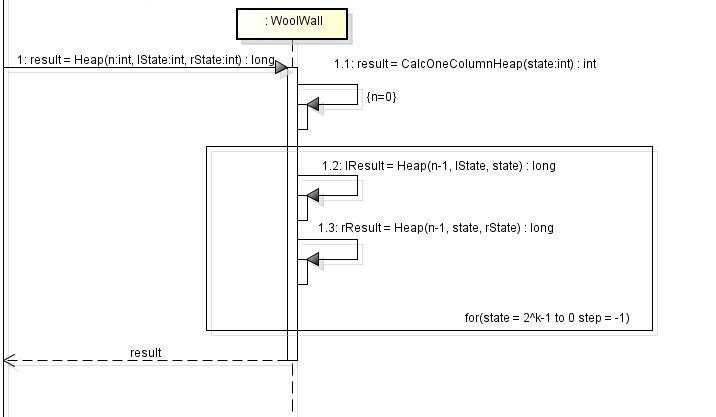
3,核心算法讲解
上图反应了Heep调用的主要方法调用,在循环中,result 累加 lResult 和 rResult。
在实际代码中,首先是从缓存中读取结果,如果没有缓存中读取结果在进行计算。
分解法分解到一列时,不在分解,直接计算机过
if (n == 0)
{
return CalcOneColumnHeapCount(lState);
}
整个程序的核心代码
for (int state = 0; state <= maxState; state++)
{
if (n == 1)
{
if (!StateIsAvailable(n, lState, rState, state))
{
continue;
}
result += Heap(n - 1, state | lState, state | lState) *
Heap(n - 1, state | rState, state | rState);
}
else
{
result += Heap(n - 1, lState, state)
* Heap(n - 1, state, rState);
}
result %= 1000000007;
}
通过for循环,求和state=0到state=2^k-1的两边木墙乘积。
当n=1切分时,需要特殊考虑。如下图:
图2-7
看上图中,因为左边墙中间被绿色方块占用,所以在(1,0)-(1,1)这个位置不能再放绿色方块。所以一些状态需要排除,如state=2需要排除。同时在还需要合并状态,如state=1时,左边墙的状态=3。
CalcOneColumnHeap(int state)函数用于计算一列时摆放方案数。
计算方法是, 求和被绿色木块分割开的每一段连续方格的摆放方案数。每一段连续的方格的摆放方案通过CalcAllState方法求得。经过分析,可以得知CalcAllState是类似斐波那契序列的函数。
如:state = 4546(当然题目中state最大=15,这里只是为了演示如何计算),二进制是:1000111000010。位置上为1,表示被绿色木块占用,0表示空着,可以自由摆放。
1000111000010 被分割后 1 000 111 0000 1 0, 那么就有 000=3个连续位置, 0000=4个连续位置 , 0=1个连续位置,。堆放结果=CalcAllState(3) + CalcAllState(4) + CalcAllState(1) = 3 + 5 + 1 = 9;
三、优化算法。正向推导,减少调用次数
上面的性能不是很高,是因为调用性能的树形结构,形成了大量的函数调用和缓存查找, 为了得到更高的性能,可以通过新的解决思路。那就是所有的运算直接依赖于上一次运算的结果,这样可以防止更多的调用。如果每次运算都算出所有边界状态的结果,那么就能为下一次运算提供足够的信息。
下面是根这种思想编写的代码,
1024,4执行时间70ms左右以内
using System;
using System.Collections.Generic;
using System.Text;
namespace HeapBlock
{
public class HeapTheWall
{
private int n;
private int height;
private int maxState;
public HeapTheWall(int n, int height)
{
this.n = n;
this.height = height;
maxState = (1 << height) - 1;
}
public static int Heap(int n, int k)
{
return new HeapTheWall(n, k).Heap();
}
public int Heap()
{
int[,] result = new int[maxState + 1, maxState + 1];
int[,] prevResult = new int[maxState + 1, maxState + 1];
Heap(n, result, prevResult);
return result[0, 0];
}
private void Heap(int n, int[,] result, int[,] prevResult)
{
if (n == 0)
{
CalcOneColumnResult(result);
return;
}
Heap(n - 1, prevResult, result);
for (int lState = 0; lState <= maxState; lState++)
{
for (int rState = 0; rState <= lState; rState++)
{
CalcResult(prevResult, result, lState, rState);
result[rState, lState] = result[lState, rState];
}
}
}
private void CalcOneColumnResult(int[,] result)
{
for (int i = 0; i <= maxState; i++)
{
for (int j = 0; j <= maxState; j++)
{
result[i, j] = ((i | j) != i + j) ? 0 : CalcOneColumnHeap(i + j);
}
}
}
private void CalcResult(int[,] prevResult, int[,] result, int lState, int rState)
{
result[lState, rState] = 0;
for (int middState = 0; middState <= maxState; middState++)
{
result[lState, rState] = (int)((result[lState, rState] + 1L * prevResult[lState, middState] * prevResult[middState, rState]) % 1000000007);
}
}
private int CalcOneColumnHeap(int state)
{
int result = 1;
foreach (int serialCount in GetAllSerialFreeCellCount(state))
{
result *= CalcAllState(serialCount);
}
return result;
}
private List<int> GetAllSerialFreeCellCount(int state)
{
List<int> result = new List<int>();
int serialCountn = 0;
for (int idx = 0; idx < height; idx++)
{
if ((state & 1) == 0)
{
serialCountn++;
}
else
{
if (serialCountn > 0)
{
result.Add(serialCountn);
}
serialCountn = 0;
}
state >>= 1;
if (idx == height - 1)
{
if (serialCountn > 0)
{
result.Add(serialCountn);
}
}
}
return result;
}
private static int CalcAllState(int n)
{
return n <= 2 ? n : CalcAllState(n - 1) + CalcAllState(n - 2);
}
}
}
1,如何调用?
HeapTheWall.Heap(100,4);//直接通过静态方法调用
new HeapTheWall(100,4).Heap();//通过构造对象,然后调用实例方法
2,思路
创建两个数组,一个用于存放当前计算的,一个用于存放上一次计算的结果。这个数组除了包含墙的堆放结果(这其实就是边界状态为0,0是的堆放结果),还包括所有不同边界状态时的堆放结果。
如果f(n,k)要直接依赖于f(n-1,k)的结果,那么f(n,k)每次计算就需要计算出左右边界状态所有组合情况的堆放数。
此思路,首先计算出n=0时的结果,然后计算n=1时的结果,以此类推。
3,代码解释
public int Heap()
{
int[,] result = new int[maxState + 1, maxState + 1];
int[,] prevResult = new int[maxState + 1, maxState + 1];
Heap(n, result, prevResult);
return result[0, 0];
}
构造两个数组,一个用于存放零时结果(上一次的结果),一个用于存放最终计算结果。result[0,0] 存放状态(0,0) 的堆放方案数,result[lState,rState],返回状态(lState,rState)时墙的堆放方案数。
private void Heap(int n, int[,] result, int[,] prevResult)
{
if (n == 0)
{
CalcOneColumnResult(result);
return;
}
Heap(n - 1, prevResult, result);
for (int lState = 0; lState <= maxState; lState++)
{
for (int rState = 0; rState <= lState; rState++)
{
CalcResult(prevResult, result, lState, rState);
result[rState, lState] = result[lState, rState];
}
}
}
如果n == 0,直接计算出结果,如果n > 1 是,首先计算出 n-1 的结果。两个for循环则是遍历左右边界的所有状态组合,然后调用CalcResult方法,计算每种边界状态的结果,然后写入到结果数组中。





 本文介绍了一种木块砌墙算法的实现,包括遍历法、递归分解法及优化后的正向推导算法。通过C#代码展示了不同方法的具体实现细节。
本文介绍了一种木块砌墙算法的实现,包括遍历法、递归分解法及优化后的正向推导算法。通过C#代码展示了不同方法的具体实现细节。

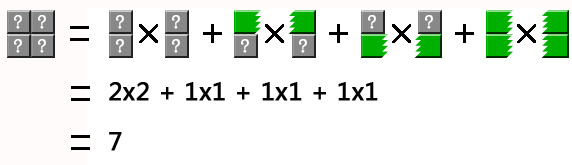
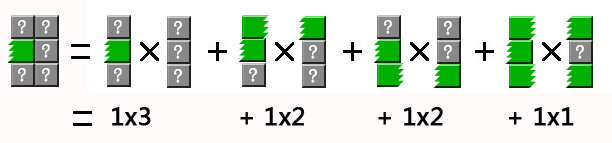
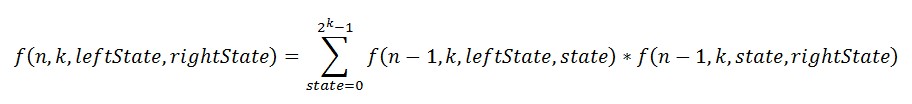

















 1915
1915

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








