User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) where a1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only if Ai, j = 1.
Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.
The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.
The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1and n occurs exactly once in the given permutation.
Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of thei-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.
In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
7 5 2 4 3 6 7 1 0001001 0000000 0000010 1000001 0000000 0010000 1001000
1 2 4 3 6 7 5
5 4 2 1 5 3 00100 00011 10010 01101 01010
1 2 3 4 5
In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).
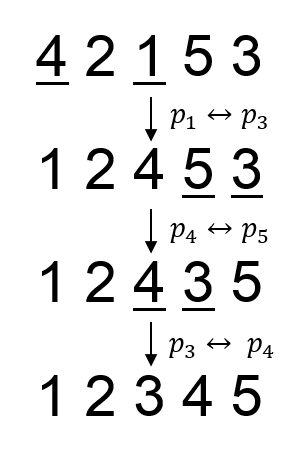
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).
A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. Thei-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.
题意:
给你一个数列,如何经过互换得到一个字典序最小的数列。互换必须依据一定规则,再给出的n*n矩阵上,若Ai,j为1则表示第i个数字与第j个数字可以互换。注意所给矩阵不一定是对称的,但是只要为1就说明可以互换。
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 305
using namespace std;
int A[MAXN][MAXN];
int n;
int arr[MAXN];
char s[MAXN];
int main(){
scanf("%d", &n);
for(int i = 0; i < n; ++i){
scanf("%d", &arr[i]);
}
for(int i = 0; i < n; ++i){
cin >> s;
for(int j = 0; j < n; ++j){
A[i][j] = s[j] - '0';
}
}
//Floyed注意k的位置
for(int k = 0; k < n; ++k){
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j){
//A[i][j]与或(A[i][k] 与 A[k][j])
A[i][j] |= A[i][k] & A[k][j];
}
}
}
for(int i = 0; i < n; ++i){
for(int j = i + 1; j < n; ++j){
//把大的换到后面
if(A[i][j] && (arr[i] > arr[j])){
swap( arr[i],arr[j] );
}
}
}
for(int i = 0; i < n; ++i){
printf("%d ", arr[i]);
}
return 0;
}并查集:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 305
using namespace std;
int n;
int father[MAXN];
int arr[MAXN];
bool m_union(int x,int y);
int m_father(int x);
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
scanf("%d", &arr[i]);
father[i] = i;
}
getchar();
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
char c;
scanf("%c",&c);
//每次按位读入,关系是1的两点就绑定起来,操作就是常规的并查集绑定操作
if((c - '0') == 1)
m_union( i,j );
}
getchar();
}
/** \brief
*
* \因为通常我们在进行绑定时都是双层for循环遍历,但是在输入时只有1的点才会绑定
* \会漏掉很大一部分情况。比如可能会出现一些根节点在最后并入某个根节点,而最初
* \根节点以下的点就不能得到遍历,所以这里需要在更新一遍。
*
*/
for(int i=1; i <= n; i++)
father[i]=m_father(i);
for(int i = 1; i <= n; i++)
{
for(int j = i+1; j <= n; j++)
{
if((father[i] == father[j]) && (arr[i] > arr[j]))
swap(arr[i],arr[j]);
}
}
for(int i = 1; i <= n; i++)
{
if( i != n)
printf("%d ",arr[i]);
else
printf("%d\n",arr[i]);
}
return 0;
}
bool m_union(int x,int y)
{
int x1=m_father(x);
int x2=m_father(y);
if(x1 != x2)
father[x2]=x1;
return true;
}
int m_father(int x)
{
if(x!=father[x])
father[x]=m_father(father[x]);
return father[x];
}























 628
628

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








