一,一维信号的拓延
在Mallat算法的推导中,假定输入序列是无限长的,而实际应用中常常是分时采样,即输入序列为有限长.此时,滤波器系数与输入序列卷积时就会出现轮空的现象.因此有必要对原始信号进行边界延拓,减小边界误差.解决的方法通常有补零法和周期延拓法.
1)补零法是在输入序列的末尾补零.补零法的缺点是可能人为造成输入序列边界的不连续,从而使得较高频率的小波系数很大.
2)周期延拓法是将原来有限长的输入序列拓展成周期的序列.周期延拓可适用于任何小波变换,但可能导致输入序列边缘的不连续,使得高频系数较大.这种方式的拓延卷积后与源信号的长度一致。
3)对称延拓(matlab默认采取这种方式)可避免输入序列边缘的不连续,但只适用于对称小波变换.本文根据Mallat算法公式,编写了对称延拓方式的小波变换的一般实现方法.
注:笔者采用的编译器为VS2013,当前系统为win10。
1,常见的3种边缘拓延方法
设输入信号为f(n),长度为srcLen,滤波器长度为filterLen.下面给出信号边界处理几种方法的具体表达式如下:
1)周期拓延:
f(n+ srcLen) , -(filterLen -1)≤ n< 0
f′(n)= f(n) , 0≤ n≤ srcLen -1
f(n -srcLen) , srcLen -1< n≤srcLen+filterLen -2
举例说明:以“1 2 3 4 5 6 7 8”这个长度为8的信号为例,当滤波器的长度为4时,其具体的拓延长度为6(单边为3):
6 7 8 (1 2 3 4 5 6 7 8)1 2 3
2)对称延拓(本文重点)
f(-n -1) , -(filterLen-1)≤ n< 0
f′(n)= f(n) , 0≤ n≤srcLen-1
f(2srcLen -n -1) , srcLen-1< n≤ srcLen+ filterLen-2
举例说明:以“1 2 3 4 5 6 7 8”这个长度为8的信号为例,当滤波器的长度为4时,其具体的拓延长度为6(单边为3):
3 2 1 (1 2 3 4 5 6 7 8)8 7 6
3)零值填补
0 , -(filterLen -1)≤ n< 0
f′(n)= f(n) , 0≤ n≤srcLen -1
0 , srcLen -1< n≤srcLen+filterLen -2
举例说明:以“1 2 3 4 5 6 7 8”这个长度为8的信号为例,当滤波器的长度为4时,其具体的拓延长度为6(单边为3):
0 0 0 (1 2 3 4 5 6 7 8)0 0 0
二,Mallat算法分解过程
在Mallat算法中,信号分解过程按照系数形式,
其中:hd(n)和gd(n)分别为分解的低通和高通滤波器系数,长度为filterLen .
吐槽:信号滤波的过程其实就是滤波器与信号卷积的过程,也就是滤波器的频谱和信号的频谱相乘的过程。
那么低通滤波器频谱是高频低,低频高,与信号相乘时高频的会被过滤掉;高通滤波器同理!
1,详细的单级分解过程
以db2小波为例,通过对称拓延后的详细计算过程如下:
从上图可知,小波的Mallat算法分解后的序列长度由原序列长srcLen和滤波器长filterLen决定。从Mallat算法(采用对称拓延)的分解原理可知,分解后的序列就是原序列与滤波器序列的卷积再进行隔点抽取而来。即分解抽取的结果长度为(srcLen+filterLen-1)/2。
上述方法也是matlab默认采取的方法,在MATLAB中输入代码,查看结果便知:
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('db2');%获取小波系数
xx=[420.2, 423.53, 423.52, 423.35, 424.52, 428, 430.79, 428.92];
wname='db2';
level=1;
[c,l]=wavedec(xx,level,wname);%进行一层分解matlab计算结果为(被存储在系数矩阵c中,l记录的是每段系数的长度):
595.429871699852 597.374655846484 598.449909371632 604.108998389031607.245626013478
-2.03920021086643 0.509501871423169-1.289053089583672.33989974581161 -1.14513645475084
与上图(来自参考论文)一致
2,C++实现单级分解算法
获取db2小波系数:
//系数精度很高,采自matlab
extern double db2_Lo_D[4] = { -0.129409522550921, 0.224143868041857, 0.836516303737469, 0.482962913144690 };
extern double db2_Hi_D[4] = { -0.482962913144690, 0.836516303737469, -0.224143868041857, -0.129409522550921 };
extern double db2_Lo_R[4] = { 0.482962913144690, 0.836516303737469, 0.224143868041857, -0.129409522550921 };
extern double db2_Hi_R[4] = { -0.129409522550921, -0.224143868041857, 0.836516303737469, -0.482962913144690 };
// 一维信号的小波分解
int CWavelet::DWT(
double *pSrcData,//分解的源信号
int srcLen,//源信号的长度
double *pDstCeof//分解出来的,本函数将返回此长度
)
{
//本程序禁止出现这种情况,否则数据出错(对称拓延长度为filterLen-1,如果大于了signalLen将越界)
if (srcLen < m_dbFilter.filterLen - 1)
{ //实际上信号的长度可以是任意的(matlab顺序:信号拓延-》卷积-》下采样),
//但是本程序为了算法速度,写法上不允许
cerr << "错误信息:滤波器长度大于信号!" << endl;
Sleep(1000);
exit(1);
}
int exLen = (srcLen + m_dbFilter.filterLen - 1) / 2;//对称拓延后系数的长度
int k = 0;
double tmp = 0.0;
for (int i = 0; i < exLen; i++)
{
pDstCeof[i] = 0.0;
pDstCeof[i + exLen] = 0.0;
for (int j = 0; j < m_dbFilter.filterLen; j++)
{
k = 2 * i - j + 1;
//信号边沿对称延拓
if ((k<0) && (k >= -m_dbFilter.filterLen + 1))//左边沿拓延
tmp = pSrcData[-k - 1];
else if ((k >= 0) && (k <= srcLen - 1))//保持不变
tmp = pSrcData[k];
else if ((k>srcLen - 1) && (k <= (srcLen + m_dbFilter.filterLen - 2)))//右边沿拓延
tmp = pSrcData[2 * srcLen - k - 1];
else
tmp = 0.0;
pDstCeof[i] += m_dbFilter.Lo_D[j] * tmp;
pDstCeof[i + exLen] += m_dbFilter.Hi_D[j] * tmp;
}
}
return 2 * exLen;
}
附带测试主函数:
int main()
{
system("color 0A");
double s[8] = { 420.2, 423.53, 423.52, 423.35, 424.52, 428, 430.79, 428.92};
int signalLen = sizeof(s) / sizeof(double);
cout << "原始信号:" << endl;
for (int i = 0; i < signalLen; i++)
cout << s[i] << " ";
cout << endl;
CWavelet cw(2);
double *dst = new double[10];
cw.DWT(s, signalLen,dst);
cout << "分解后的系数:" << endl;
for (int i = 0; i < 10; i++)
cout << dst[i] << " ";
cout << endl;
delete[] dst;
dst = NULL;
system("pause");
return 0;
}
三,Mallat单级重构过程

1,详细的单级重构过程
以db2小波为例,通过对称拓延后的详细重构过程如下:
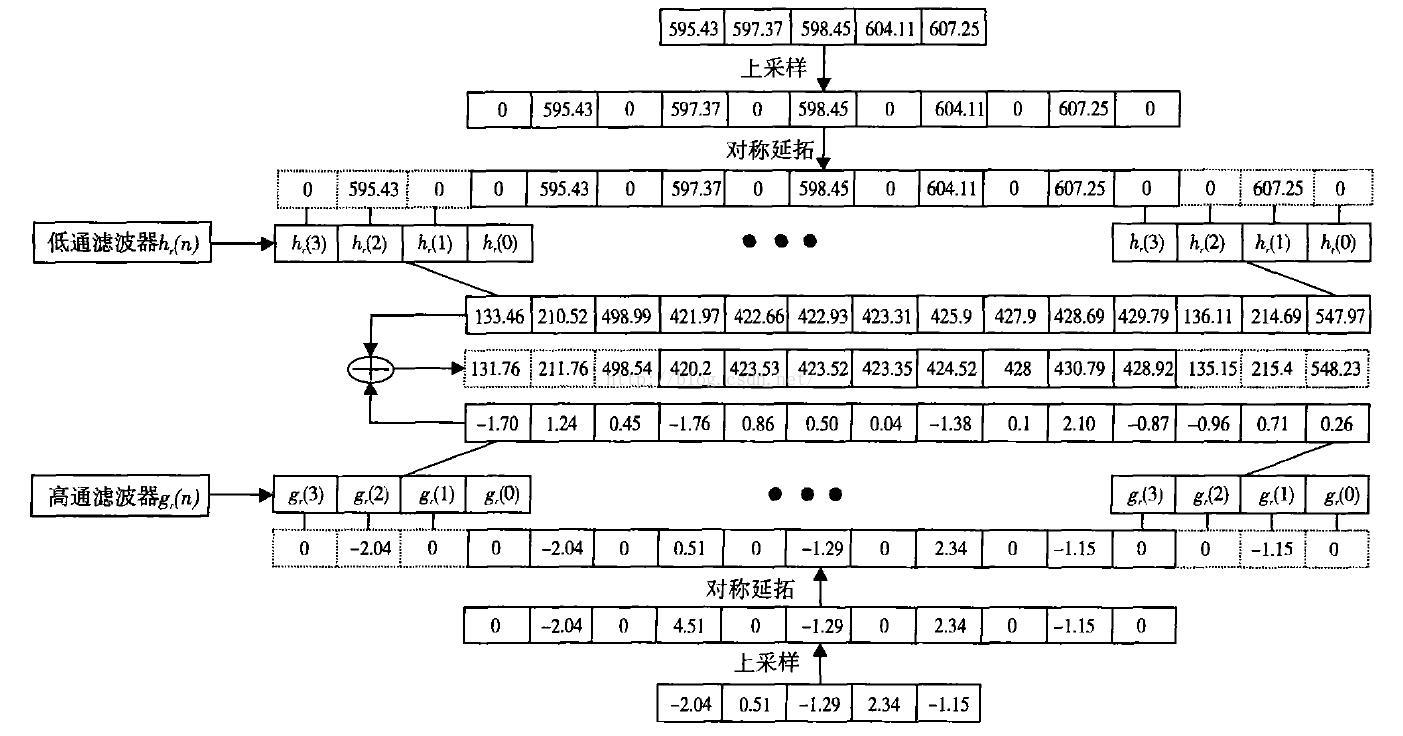
在matlab中我们可以通过以下代码实现重构(完全实现原信号)
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('db2');%获取小波系数
xx=[420.2, 423.53, 423.52, 423.35, 424.52, 428, 430.79, 428.92];
wname='db2';
level=1;
[c,l]=wavedec(xx,level,wname);%进行一层分解
cc=waverec(c,l,wname);2,C++实现单级重构算法
// 一维小波反变换,重构出源信号
void CWavelet::IDWT(
double *pSrcCoef,//源分解系数
int dstLen,//重构出来的系数的长度
double *pDstData//重构出来的系数
)
{
int p = 0;
int caLen = (dstLen + m_dbFilter.filterLen - 1) / 2;
for (int i = 0; i < dstLen; i++)
{
pDstData[i] = 0.0;
for (int j = 0; j < caLen; j++)
{
p = i - 2 * j + m_dbFilter.filterLen - 2;
//信号重构
if ((p >= 0) && (p<m_dbFilter.filterLen))
pDstData[i] += m_dbFilter.Lo_R[p] * pSrcCoef[j] + m_dbFilter.Hi_R[p] * pSrcCoef[j + caLen];
}
}
}
附带测试主函数:
int main()
{
system("color 0A");
double s[8] = { 420.2, 423.53, 423.52, 423.35, 424.52, 428, 430.79, 428.92};
int signalLen = sizeof(s) / sizeof(double);
cout << "原始信号:" << endl;
for (int i = 0; i < signalLen; i++)
cout << s[i] << " ";
cout << endl;
CWavelet cw(2);
double *dst = new double[10];
cw.DWT(s, signalLen,dst);
cout << "分解后的系数:" << endl;
for (int i = 0; i < 10; i++)
cout << dst[i] << " ";
cout << endl;
double *dstsrc = new double[signalLen];
cw.IDWT(dst, signalLen, dstsrc);
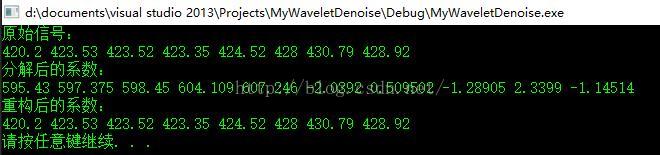
cout << "重构后的系数:" << endl;
for (int i = 0; i < signalLen; i++)
cout << dstsrc[i] << " ";
cout << endl;
delete[] dstsrc;
dstsrc = NULL;
delete[] dst;
dst = NULL;
system("pause");
return 0;
}
程序中所有用到的结构体等信息的头文件声明如下:
#ifndef _WAVELET_H_
#define _WAVELET_H_
#include <vector>
using namespace std;
namespace wavelet
{
//小波滤波器
typedef struct tagWaveFilter
{
vector<double> Lo_D; // 小波变换分解低通滤波器
vector<double> Hi_D; // 小波变换分解高通滤波器
vector<double> Lo_R; // 小波变换重构低通滤波器
vector<double> Hi_R; // 小波变换重构高通滤波器
int filterLen;
}WaveFilter;
typedef struct tagCL1D
{//本结构体用于接收一维图像分解信息,避免参数的大量传送
vector<int> msgLen;
int Scale;//分解尺度
int dbn;//db小波的编号
int allSize;//总数据长度
}msgCL1D;
typedef struct tagCL2D
{//本结构体用于接收二维图像分解信息,避免参数的大量传送
vector<int> msgHeight;
vector<int> msgWidth;
int Scale;//分解尺度
int dbn;//db小波的编号
int allSize;//总数据长度
}msgCL2D;
typedef bool SORH;
class CWavelet
{
public:
CWavelet(int dbn=3);
~CWavelet();
int DWT(
double *pSrcData,
int srcLen,
double *pDstCeof
);
void IDWT(double *pSrcCoef,
int dstLen,
double *pDstData
);
// 二维数据的小波分解
void DWT2(
double *pSrcImage,//源图像数据(存储成一维数据,行优先存储)
int height,//图像的高
int width,//图像的宽
double *pImagCeof//分解出来的系数
);
void IDWT2(
double *pSrcCeof,
int height,
int width,
double *pDstImage
);
bool WaveDec(
double *pSrcData,
double *pDstCeof
);
bool WaveRec(
double *pSrcCoef,
double *pDstData
);
bool InitDecInfo(
const int srcLen,
const int Scale,
const int dbn =3
);
bool InitDecInfo2D(
const int height,
const int width,
const int Scale,
const int dbn = 3
);
bool thrDenoise(
double *pSrcNoise,
double *pDstData,
bool isHard=true
);
void Wthresh(
double *pDstCoef,
double thr,
const int allsize,
const int gap,
SORH ish
);
// 二维小波多级分解
bool WaveDec2(
double *pSrcData,
double *pDstCeof
);
// 重构出二维信号
bool WaveRec2(
double *pSrcCoef,//多级分解出的源系数
double *pDstData//重构出来的信号
);
// 初始化滤波器
void InitFilter();//放进内存
// 选择滤波器
void SetFilter(int dbn);
// 获取阈值
double getThr(
double *pDetCoef,
int detlen,
bool is2D =false
);
//调整数据,总是将低频数据放在前面
bool AdjustData(
double *pDetCoef,
const int height,//该系数的高度
const int width//该系数的宽度
);
//逆调整,还原低频数据的位置
bool IAdjustData(
double *pDetCoef,
const int height,//该系数的高度
const int width//该系数的宽度
);
bool thrDenoise2D(
double *pNoiseImag,//噪声图像
double *pDstImag,//已经去噪的图像
bool isHard = true);
public:
msgCL1D m_msgCL1D;
msgCL2D m_msgCL2D;
private:
bool m_bInitFlag1D; //是否初始化的标志
bool m_bInitFlag2D; //是否初始化的标志
WaveFilter m_dbFilter;//分解滤波器
};
}
#endif
参考资源:
【1】乔世杰.小波图像编码中的对称边界延拓法[ J].中国图像图形学报,2000,5(2):725-729.




























 1002
1002

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








