一,二叉树的基本概念:
1,二叉搜索树的简单概念
二叉搜索树的任意节点最多有两个子节点。
二叉搜索树(BinarySearch Tree,也叫二叉查找树,或称二叉排序树BinarySort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
(1)、若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
(2)、若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
(3)、它的左、右子树也分别为二叉查找树。
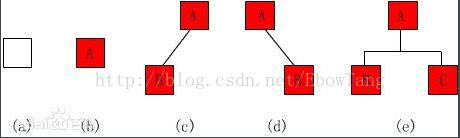
二叉树是递归定义的,其结点有左右子树之分,逻辑上二叉树有五种基本形态:
(1)空二叉树(a);
(2)只有一个根结点的二叉树(b);
(3)只有左子树(c);
(4)只有右子树(d);
(5)完全二叉树(e)。
注意:尽管二叉树与树有许多相似之处,但二叉树不是树的特殊情形
2,二叉搜索树节点设计
每个节点不但指向子节点,也指向父节点。
<pre name="code" class="html">// 二叉搜索树结点的定义
template<class DataType>
class BSTNode
{
public:
BSTNode(DataType newData)// 带参数的构造函数
{//初始化节点参数
nData = newData;
lChild = NULL;
rChild = NULL;
pParent = NULL;
}
private:
DataType nData;
BSTNode<DataType> *lChild;//左子树
BSTNode<DataType> *rChild;//右子树
BSTNode<DataType> *pParent;//父节点
friend class LinkBSTree<DataType>; // 允许二叉搜索树类对节点类的私有变量任意访问
};3,二叉搜索树类的设计
本类实现了
1)节点插入
2)前序遍历
3)后序遍历
4)中序遍历
5)计算二叉搜索树的高度
6)删除整个二叉搜索树
7)比较两个二叉搜索树是否一样
8)删除有指定关键字的节点
9)寻找指定关键字的前驱和后继指针
10)寻找最大最小关键字的节点指针
11)获取二叉搜索树的最大最小值
12)统计节点数目
13)获取指定关键字的节点指针
// 带有头结点指针的二叉搜索树类的定义
template<class DataType>
class LinkBSTree
{
public:
LinkBSTree( int size)
{
maxSize = size;
m_pRoot = NULL;
count = 0;
}
~LinkBSTree()
{
DeleteTree(m_pRoot);
}
//获取根节点指针
BSTNode<DataType> *getRoot() const
{
return m_pRoot;
}
//统计节点数目
int getCount()
{
return count;
}
//插入结点
void InsertBTNode(DataType newData);
//先序遍历
void preOrder(BSTNode<DataType> *node);
//中序遍历
void inOrder(BSTNode<DataType> *node);
//后序遍历
void postOrder(BSTNode<DataType> *node);
//删除二叉树
void DeleteTree(BSTNode<DataType> *node);
//从root节点开始查找给定关键字的节点指针
BSTNode<DataType>* SearchNode(BSTNode<DataType> *root, DataType key);
//二叉树的高度
int DepthTree(BSTNode<DataType> *root);
//求取较大值
int max(int m = 0, int n = 0);
//比较两棵树
int compareTree(BSTNode<DataType> *aNode, BSTNode<DataType> *bNode);
//从节点root开始寻找二叉搜索树的最大最小值节点
BSTNode<DataType>* SearchMaxMin(BSTNode<DataType> *root, bool isMax = true);
//查找某个结点的后继 (即比该节点关键字大的最小的关键字)
BSTNode<DataType>* SearchSuccessor(BSTNode<DataType> *node);
//查找某个结点的前驱 (即比该节点关键字小的最大的关键字)
BSTNode<DataType>* SearchPredecessor(BSTNode<DataType> *node);
//删除具有指定关键字的节点
bool DeleteNode(DataType key);
//获取二叉搜索树的最大或者最小值
DataType getMaxMin(bool isMax=true);
private:
BSTNode<DataType> *m_pRoot;//指向根节点
int count;//统计节点数目
int maxSize;//二叉搜索树的最大规模
};
二,二叉树的C++模板实现
1,BinaryTree.h中各函数的实现:
//插入节点,插入规则较小值在左边,较大值在右边
template<class DataType>
void LinkBSTree<DataType>::InsertBTNode(DataType newData)
{
if (count == maxSize)
exit(1);
BSTNode<DataType> *newNode = new BSTNode<DataType>(newData);
if (m_pRoot == NULL)
{
m_pRoot = newNode;
count++;
return;
}
BSTNode<DataType> *pPre = NULL;//用于保存上一个节点
BSTNode<DataType> *pCur = m_pRoot;
//寻找要插入的节点的位置 (一定是某个叶子)
while (pCur != NULL)
{
pPre = pCur;//保存节点
if (newNode->nData < pCur->nData)
{
pCur = pCur->lChild;//较小值则移到节点的左子树
}
else
{
pCur = pCur->rChild;
}
}
//建立连接
if (newNode->nData < pPre->nData)
{
pPre->lChild = newNode;
newNode->pParent = pPre;
count++;
}
else
{
pPre->rChild = newNode;
newNode->pParent = pPre;
count++;
}
}
//查找某个结点的后继 (即比该节点关键字大的最小的关键字)
template<class DataType>
BSTNode<DataType>* LinkBSTree<DataType>::SearchSuccessor(BSTNode<DataType> *node)
{
//右子树不为空
if (node->rChild != NULL)
return SearchMaxMin(node->rChild, false);//寻找node节点左子树中最小的节点
//右子树为空(向上寻找,找到node的某个父节点是他父节点的左子)
BSTNode<DataType> *dstnode = node->pParent;
while (dstnode != NULL && node == dstnode->rChild)//本程序根节点没有父节点
{
node = dstnode;
dstnode = dstnode->pParent;
}
return dstnode;
}
//查找某个结点的前驱 (即比该节点关键字小的最大的关键字)
template<class DataType>
BSTNode<DataType>* LinkBSTree<DataType>::SearchPredecessor(BSTNode<DataType> *node)
{
//左子树不为空
if (node->lChild != NULL)
return MaxMinTree(node->rChild);//寻找node节点左子树中最小的节点
//左子树为空(向上寻找,找到node的某个父节点是他父节点的右子)
BSTNode<DataType> *dstnode = node->pParent;
while (dstnode = !NULL && node == dstnode->lChild)//本程序根节点没有父节点
{
node = dstnode;
dstnode = dstnode->pParent;
}
return dstnode;
}
//从节点root开始寻找二叉搜索树的最大最小值节点
template<class DataType>
BSTNode<DataType>* LinkBSTree<DataType>::SearchMaxMin(BSTNode<DataType> *root, bool isMax)
{
if (root == NULL)
return NULL;
if (isMax)
{
if (root->rChild == NULL)//没有右孩子的结点
return root;//找到最大值了
else //一直往右孩子找
return SearchMaxMin(root->rChild, isMax);
}
else
{
if (root->lChild == NULL)//没有左孩子的结点
return root;//找到最小值了
else //一直往左孩子找
return SearchMaxMin(root->lChild, isMax);
}
}
//获取二叉搜索树的最大或者最小值
template<class DataType>
DataType LinkBSTree<DataType>::getMaxMin(bool isMax = true)
{
BSTNode<DataType>* dstnode = SearchMaxMin(m_pRoot, isMax);
return dstnode->nData;
}
//查找一个具有给定关键字的节点指针
template<class DataType>
BSTNode<DataType>* LinkBSTree<DataType>::SearchNode(BSTNode<DataType> *root, DataType key)
{
if (root == NULL)
return NULL;
if (root->nData == key)
return root;
if (root->nData > key)
return SearchNode(root->lChild, key);
else
return SearchNode(root->rChild, key);
}
//二叉树某一个结点的高度总是其左子树或右子树中较高的一个子树的高度再加1
//由此获得递归关系
template<class DataType>
int LinkBSTree<DataType>::DepthTree(BSTNode<DataType> *root)
{
if (root == NULL)
return 0;
else
return 1 + max(DepthTree(root->lChild), DepthTree(root->rChild));
}
//获取两者间的较大者
template<class DataType>
int LinkBSTree<DataType>::max(int m, int n)
{
if (m > n)
return m;
else
return n;
}
//删除具有指定关键字的节点,每次删除时分四种情况,并且特别注意根节点的情况
template<class DataType>
bool LinkBSTree<DataType>::DeleteNode(DataType key)
{
BSTNode<DataType> *dstnode = SearchNode(m_pRoot,key);
if (dstnode == NULL)
return false;
//1,被删除的节点是叶子则直接删除
if (dstnode->lChild == NULL&&dstnode->rChild == NULL)
{
if (dstnode->pParent == NULL)//如果这个节点是根节点
{
delete dstnode;
m_pRoot = NULL;
count--;
}
else
{
if (dstnode->pParent->lChild == dstnode)
dstnode->pParent->lChild = NULL;
else
dstnode->pParent->rChild = NULL;
delete dstnode;
dstnode = NULL;
count--;
}
}
//2,被删除的节点只有一个左节点
if (dstnode->lChild !=NULL && dstnode->rChild == NULL)
{
if (dstnode->pParent == NULL)//如果这是根节点
{
m_pRoot = dstnode->lChild;
delete dstnode;
dstnode = NULL;
count--;
}
else
{
dstnode->pParent->lChild = dstnode->lChild;
delete dstnode;
dstnode = NULL;
count--;
}
}
//3,被删除的节点只有一个右节点
if (dstnode->rChild !=NULL && dstnode->lChild == NULL)
{
if (dstnode->pParent == NULL)//如果这是根节点
{
m_pRoot = dstnode->rChild;
delete dstnode;
dstnode = NULL;
count--;
}
else
{
dstnode->pParent->rChild = dstnode->rChild;
delete dstnode;
dstnode = NULL;
count--;
}
}
//4,被删除的节点两边子树都有(有可能是根节点,但是这里不用考虑)
if (dstnode != NULL && dstnode != NULL)
{
BSTNode<DataType> *tmpnode = SearchSuccessor(dstnode);
DataType temp = tmpnode->nData;
//删除后继结点 (后继一定只有一个子节点)
DeleteNode(temp);
dstnode->nData = temp;//将当前要删除的节点改为后继节点的值
}
return true;
}
//删除二叉树中某一个结点及其所有子节点,可以总是先删除最底层的结点(自底向上的删除过程)
//由此获得递归关系
template<class DataType>
void LinkBSTree<DataType>::DeleteTree(BSTNode<DataType> *node)
{
if (node == NULL)
{
return;
}
else
{
DeleteTree(node->lChild);
DeleteTree(node->rChild);
delete node;
node = NULL;
}
}
template<class DataType>
void LinkBSTree<DataType>::preOrder(BSTNode<DataType> *node)
{
if (node != NULL)
{
cout << node->nData << " ";//输出根结点
preOrder(node->lChild);//遍历左子树
preOrder(node->rChild);//遍历右子树
}
}
template<class DataType>
void LinkBSTree<DataType>::inOrder(BSTNode<DataType> *node)
{
if (node != NULL)
{
inOrder(node->lChild);
cout << node->nData << " ";//输出根结点
inOrder(node->rChild);
}
}
template<class DataType>
void LinkBSTree<DataType>::postOrder(BSTNode<DataType> *node)
{
if (node != NULL)
{
postOrder(node->lChild);
postOrder(node->rChild);
cout << node->nData << " ";//输出根结点
}
}
template<class DataType> //本处代码有问题
int LinkBSTree<DataType>::compareTree(BSTNode<DataType> *aTreeNode, BSTNode<DataType> *bTreeNode)
{
bool IsaTreeNull = (aTreeNode == NULL);//如果atree为空则Istreenull为真
bool IsbTreeNull = (bTreeNode == NULL);
if (IsaTreeNull != IsbTreeNull)
{
return 1;//两棵树不一样
}
if (IsaTreeNull && IsbTreeNull)
{
return 0;
}
if (aTreeNode->nData != bTreeNode->nData)
{
return 1;
}
//注意两棵树如果不是遵循同一个结点插入原则,还要添加a树左子树与b树右子树的比较
return (compareTree(aTreeNode->lChild, bTreeNode->lChild) | compareTree(aTreeNode->rChild, bTreeNode->rChild));
}2,主测试函数:
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
#include "BinaryTree.h"
#include "time.h"
#include "iostream"
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
system("color 0A");
LinkBSTree<char> aTree(1024);
aTree.InsertBTNode('C');
aTree.InsertBTNode('D');
aTree.InsertBTNode('A');
aTree.InsertBTNode('E');
aTree.InsertBTNode('F');
aTree.InsertBTNode('B');
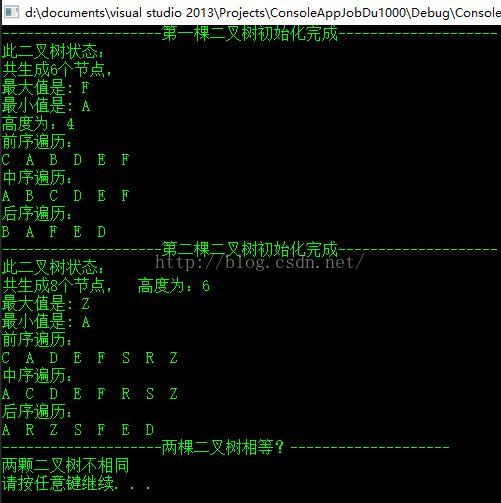
cout << "--------------------第一棵二叉树初始化完成--------------------" << endl;
cout << "此二叉树状态:"<<endl<<"共生成" << aTree.getCount() << "个节点, " << endl;
cout <<"最大值是: "<< aTree.getMaxMin() << endl;
cout << "最小值是: " << aTree.getMaxMin(false) << endl;
cout << "高度为:" << aTree.DepthTree(aTree.getRoot()) << endl;
cout << "前序遍历:" << endl;
aTree.preOrder(aTree.getRoot());
cout << endl << "中序遍历:" << endl;
aTree.inOrder(aTree.getRoot());
aTree.DeleteNode('C');
cout << endl << "后序遍历:" << endl;
aTree.postOrder(aTree.getRoot());
cout << endl;
LinkBSTree<char> bTree(1024);
bTree.InsertBTNode('C');
bTree.InsertBTNode('D');
bTree.InsertBTNode('A');
bTree.InsertBTNode('E');
bTree.InsertBTNode('F');
bTree.InsertBTNode('S');
bTree.InsertBTNode('R');
bTree.InsertBTNode('Z');
cout << "--------------------第二棵二叉树初始化完成--------------------" << endl;
cout << "此二叉树状态:"<<endl<<"共生成" << bTree.getCount() << "个节点, ";
cout << "高度为:" << bTree.DepthTree(bTree.getRoot()) << endl;
cout << "最大值是: " << bTree.getMaxMin() << endl;
cout << "最小值是: " << bTree.getMaxMin(false) << endl;
cout << "前序遍历:" << endl;
bTree.preOrder(bTree.getRoot());
cout << endl << "中序遍历:" << endl;
bTree.inOrder(bTree.getRoot());
bTree.DeleteNode('C');
cout << endl << "后序遍历:" << endl;
bTree.postOrder(bTree.getRoot());
cout << endl << "--------------------两棵二叉树相等?--------------------" << endl;
if (1 == bTree.compareTree(aTree.getRoot(), bTree.getRoot()))
{
cout << "两颗二叉树不相同" << endl;
}
else
{
cout << "两棵树一样" << endl;
}
system("pause");
return 0;
}3,测试结果:
三,小试牛刀
1,二叉树的深度
- 题目描述:
-
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
- 输入:
-
第一行输入有n,n表示结点数,结点号从1到n。根结点为1。 n <= 10。
接下来有n行,每行有两个个整型a和b,表示第i个节点的左右孩子孩子。a为左孩子,b为右孩子。当a为-1时,没有左孩子。当b为-1时,没有右孩子。
- 输出:
-
输出一个整型,表示树的深度。
- 样例输入:
-
32 3-1 -1-1 -1
- 样例输出:
-
2
#include "queue"
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
using namespace std;
// 节点定义
class BSTNode
{
public:
BSTNode()// 默认构造
{
pRight = NULL;
pLeft = NULL;
value = 0;
}
friend class LinkBST;// 允许链表类随意访问节点数据
private:
int value;
BSTNode *pRight;
BSTNode *pLeft;
};
// 不带头结点的二叉树定义
class LinkBST
{
public:
LinkBST(int size)
{
m_pNode = new BSTNode[size+1];
}
~LinkBST()
{
delete[] m_pNode;
m_pNode = NULL;
}
// 连接节点集(形成一棵树)
void LinkBSTNode(int lvlaue, int rvalue, int pos);
// 计算树的深度
int DepthTree(BSTNode *&pRoot);
// 节点集
BSTNode *m_pNode;
};
// 连接节点集(形成一棵树)
void LinkBST::LinkBSTNode(int lnode, int rnode, int pos)
{
if (lnode != -1)
m_pNode[pos].pLeft = &m_pNode[lnode];
if (rnode != -1)
m_pNode[pos].pRight = &m_pNode[rnode];
}
// 计算树的深度
int LinkBST::DepthTree(BSTNode *&pRoot)
{
if (pRoot == NULL)
return 0;
else
return 1 + max(DepthTree(pRoot->pLeft), DepthTree(pRoot->pRight));
}
int main()
{
int n = 0;
while (cin >> n)
{
BSTNode *pRoot = NULL;
LinkBST bst(n);
pRoot = &bst.m_pNode[0];//指向根节点
int nleftnode = 0, nrightnode = 0;
//插入节点
for (int i = 0; i < n; i++)
{
cin >> nleftnode >> nrightnode;
if (nleftnode>n || nrightnode > n)
exit(1);
bst.LinkBSTNode(nleftnode, nrightnode, i);//第i个节点指向第nleftnode个节点和第nrightnode节点
}
cout << bst.DepthTree(pRoot) << endl;
}
}
2,二叉树遍历
-
题目描述:
-
二叉树的前序、中序、后序遍历的定义:
前序遍历:对任一子树,先访问跟,然后遍历其左子树,最后遍历其右子树;
中序遍历:对任一子树,先遍历其左子树,然后访问根,最后遍历其右子树;
后序遍历:对任一子树,先遍历其左子树,然后遍历其右子树,最后访问根。
给定一棵二叉树的前序遍历和中序遍历,求其后序遍历(提示:给定前序遍历与中序遍历能够唯一确定后序遍历)。
-
输入:
-
两个字符串,其长度n均小于等于26。
第一行为前序遍历,第二行为中序遍历。
二叉树中的结点名称以大写字母表示:A,B,C....最多26个结点。
-
输出:
-
输入样例可能有多组,对于每组测试样例,
输出一行,为后序遍历的字符串。
-
样例输入:
-
ABC BAC FDXEAG XDEFAG
-
样例输出:
-
BCA XEDGAF
#include <iostream>
#include "string"
using namespace std;
//节点定义
class BSTNode
{
public:
BSTNode(int ndata)//有参数的构造
{//函数参数表中的形参允许有默认值,但是带默认值的参数需要放后面
pRight = NULL;
pLeft = NULL;
value = ndata;
}
friend class LinkBST;//允许链表类随意访问节点数据
private:
char value;
BSTNode *pRight;
BSTNode *pLeft;
};
// 不带头结点的二叉树定义
class LinkBST
{
public:
LinkBST(){}
~LinkBST(){}
//后序遍历
void postOrder(BSTNode *pNode);
//重建二叉树
void ReBuildBST(const string &preStr, const string &midStr, BSTNode *&proot);
};
//Tips:
//int *a;int * &p = a;
//很容易理解,把 int * 看成一个类型,a就是一个整型指针,p 是a的别名,那么a与p就完全等同了
void LinkBST::ReBuildBST(const string &preStr, const string &midStr, BSTNode *&proot)
{//注意:proot是引用,要不然函数返回会对proot的内容进行撤销
if (preStr.size() == 0)
return;
proot = new BSTNode(0);
proot->value = preStr[0];//prestr[0]肯定是当前二叉树的根
proot->pLeft = NULL;
proot->pRight = NULL;
if (preStr.size() == 1)
return;
int k = midStr.find(preStr[0]);//找到字符出现的第一个位置
string preLeft = preStr.substr(1, k);
string midLeft = midStr.substr(0, k);
ReBuildBST(preLeft, midLeft, proot->pLeft);
string preRight = preStr.substr(k + 1, preStr.size() - k - 1);
string midRight = midStr.substr(k + 1, midStr.size() - k - 1);
ReBuildBST(preRight, midRight, proot->pRight);
}
void LinkBST::postOrder(BSTNode *pNode)
{
if (pNode != NULL){
postOrder(pNode->pLeft);
postOrder(pNode->pRight);
cout << pNode->value;
}
}
int main()
{
string preStr, midStr;
while (cin >> preStr >> midStr)
{
BSTNode *pRoot = NULL;
LinkBST bst;
bst.ReBuildBST(preStr, midStr, pRoot);
bst.postOrder(pRoot);
cout << endl;
}
}3,二叉树的子树节点个数
- 题目描述:
-

如上所示,由正整数1,2,3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是,结点m所在的子树中一共包括多少个结点。
比如,n = 12,m = 3那么上图中的结点13,14,15以及后面的结点都是不存在的,结点m所在子树中包括的结点有3,6,7,12,因此结点m的所在子树中共有4个结点。
- 输入:
-
输入数据包括多行,每行给出一组测试数据,包括两个整数m,n (1 <= m <= n <= 1000000000)。最后一组测试数据中包括两个0,表示输入的结束,这组数据不用处理。
- 输出:
-
对于每一组测试数据,输出一行,该行包含一个整数,给出结点m所在子树中包括的结点的数目。
- 样例输入:
-
3 120 0
- 样例输出:
-
4
#include <iostream>
#include "stack"
#include <cmath>
using namespace std;
//先不算最后一层,统计出节点数
//算出最后一层有多少节点
int main()
{
int m, n, i;
while (cin>>m>>n)
{
if (m == 0 && n == 0)
break;
//注意这里的log是以2为低
int h1 = (int)(log(m) / log(2)) + 1; // m的树高,以题举例:h1=2
int h2 = (int)(log(n) / log(2)) + 1; // n的树高,h2=4
int left = m;//3
int right = m;//3
int count = 0;//记录节点数
int h = h2 - h1; // 结点n与结点m的高度差
count = pow(2, h) - 1; //先不算最后一层,计算结点m所拥有的子节点数
for (i = 1; i <= h; i++)
{//算出节点m在共有n个节点时的最左最右节点位置
left = 2 * left;
right = 2 * right + 1;
}
//求出最后一层结点m的可能最左与最右结点
if (right <= n)
count += right - left + 1;
else if (left <= n)
count += n - left + 1;
cout << count << endl;
}
return 0;
}4,重建二叉树
- 题目描述:
-
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并输出它的后序遍历序列。

- 输入:
-
输入可能包含多个测试样例,对于每个测试案例,
输入的第一行为一个整数n(1<=n<=1000):代表二叉树的节点个数。
输入的第二行包括n个整数(其中每个元素a的范围为(1<=a<=1000)):代表二叉树的前序遍历序列。
输入的第三行包括n个整数(其中每个元素a的范围为(1<=a<=1000)):代表二叉树的中序遍历序列。
- 输出:
-
对应每个测试案例,输出一行:
如果题目中所给的前序和中序遍历序列能构成一棵二叉树,则输出n个整数,代表二叉树的后序遍历序列,每个元素后面都有空格。
如果题目中所给的前序和中序遍历序列不能构成一棵二叉树,则输出”No”。
- 样例输入:
-
81 2 4 7 3 5 6 84 7 2 1 5 3 8 681 2 4 7 3 5 6 84 1 2 7 5 3 8 6
- 样例输出:
-
7 4 2 5 8 6 3 1 No
#include "string"
#include "vector"
#include "iostream"
using namespace std;
int count_node;
typedef struct _Node
{
int value;
struct _Node *pRight;
struct _Node *pLeft;
}Node;
int findPos(const vector<int> &vec, int a)//找到整数a在数组vec中的位置
{
if (vec.size()==0)
return -1;
for (int i = 0; i < vec.size();i++)
{
if (vec[i]==a)
return i;
}
return -2;
}
//Tips:
//int *a;int * &p = a;
//很容易理解,把 int * 看成一个类型,a就是一个整型指针,p 是a的别名,那么a与p就完全等同了
void ReBuildBST(const vector<int> &preVec, const vector<int> &midVec, Node *&proot)
{//注意:proot是引用,要不然函数返回会对proot的内容进行撤销
if (preVec.size() == 0)
return;
proot = new Node;
proot->value = preVec[0];//prestr[0]肯定是当前二叉树的根
proot->pLeft = NULL;
proot->pRight = NULL;
count_node++;
if (preVec.size() == 1)
return;
//因为是互不相同的数据,所以直接判断prevec中的每一个数据是否一定能在midvec找到即可
for (int i = 0; i < preVec.size();i++)
{
bool flag = false;
for (int j = 0; j < midVec.size();j++)
{
if (preVec[i] == midVec[j])
flag = true;
}
if (flag==false)
return;
}
int k = findPos(midVec,preVec[0]);
vector<int> preLeft(preVec.begin() + 1, preVec.begin() + k + 1);
vector<int> midLeft(midVec.begin(), midVec.begin() + k);
ReBuildBST(preLeft, midLeft, proot->pLeft);
vector<int> preRight(preVec.begin()+ k + 1, preVec.end());
vector<int> midRight(midVec.begin()+ k + 1, midVec.end());
ReBuildBST(preRight, midRight, proot->pRight);
}
void postOrder(Node * root)
{
if (root != NULL){
postOrder(root->pLeft);
postOrder(root->pRight);
cout << root->value<<" ";
}
}
int main()
{
int N = 0;
while (cin >> N)
{
count_node = 0;
vector<int> preVec(N,0), midVec(N,0);
for (int i = 0; i < N; i++)
cin >> preVec[i];
for (int i = 0; i < N; i++)
cin >> midVec[i];
Node *pRoot=NULL;
ReBuildBST(preVec, midVec, pRoot);
if (count_node == N)
{
postOrder(pRoot);
cout << endl;
}
else
{
cout << "No" << endl;
}
count_node=0;
}
}5,二叉树重建及其遍历
-
题目描述:
-
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。
例如如下的先序遍历字符串:
ABC##DE#G##F###
其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
-
输入:
-
输入包括1行字符串,长度不超过100。
-
输出:
-
可能有多组测试数据,对于每组数据,
输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。
每个输出结果占一行。
-
样例输入:
-
abc##de#g##f###
-
样例输出:
-
c b e g d f a
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
using namespace std;
string preStr;
// 节点定义
class BSTNode
{
public:
BSTNode()// 默认构造
{
pRight = NULL;
pLeft = NULL;
value = 0;
}
~BSTNode();
friend class LinkBST;// 允许链表类随意访问节点数据
private:
char value;
BSTNode *pRight;
BSTNode *pLeft;
};
// 无头结点的二叉树定义
class LinkBST
{
public:
LinkBST(){};
~LinkBST(){};
// 根据字符串重建二叉树
void ReBuildTree(BSTNode *&pNode, int &index);
// 中序遍历
void InOrder(BSTNode *&pRoot);
};
// 中序遍历
void LinkBST::InOrder(BSTNode *&pNode)
{
if (pNode != NULL)
{
InOrder(pNode->pLeft);
cout << pNode->value << " ";
InOrder(pNode->pRight);
}
}
// 根据前序字符串重建二叉树
void LinkBST::ReBuildTree(BSTNode *&pNode, int &index)
{
if (index == preStr.size())
return;
if (preStr[index] == '#')
{
pNode = NULL;
index++;
}
else
{
pNode = new BSTNode;
pNode->value = preStr[index];
index++;
ReBuildTree(pNode->pLeft, index);//总是先建完左子树,再建右子树
ReBuildTree(pNode->pRight, index);
}
}
/*
a
/ \
b #
/ \
c d <------本例题的二叉树逻辑结构
/ \ / \
# # e f
/ \ / \
# g # #
/ \
# #
*/
int main()
{
while (cin >> preStr)
{
BSTNode *pRoot = NULL;
LinkBST bst;
int index = 0;
bst.ReBuildTree(pRoot,index);
bst.InOrder(pRoot);
cout << endl;
}
}6,二叉树中和为某一值的路径
- 题目描述:
-
输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
- 输入:
-
每个测试案例包括n+1行:
第一行为2个整数n,k(1<=n<=10000),n表示结点的个数,k表示要求的路径和,结点编号从1到n。
接下来有n行。这n行中每行为3个整数vi,leftnode,rightnode,vi表示第i个结点的值,leftnode表示第i个结点的左孩子结点编号,rightnode表示第i个结点的右孩子结点编号,若无结点值为-1。编号为1的结点为根结点。
- 输出:
-
对应每个测试案例,先输出“result:”占一行,接下来按字典顺序输出满足条件的所有路径,这些路径由结点编号组成,输出格式参照输出样例。
- 样例输入:
-
5 2210 2 35 4 512 -1 -14 -1 -17 -1 -11 51 -1 -1
- 样例输出:
-
result:A path is found: 1 2 5A path is found: 1 3result:
参考资源:http://my.oschina.net/u/2260265/blog/345667
#include "queue"
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
using namespace std;
// 节点定义
class BSTNode
{
public:
BSTNode()// 默认构造
{
pRight = NULL;
pLeft = NULL;
value = 0;
count = 0;
}
friend class LinkBST;// 允许链表类随意访问节点数据
private:
int value;
BSTNode *pRight;
BSTNode *pLeft;
int count;
};
// 不带头结点的二叉树定义
class LinkBST
{
public:
LinkBST(int size)
{
m_pNode = new BSTNode[size + 1];
}
~LinkBST()
{
delete[] m_pNode;
m_pNode = NULL;
}
// 连接节点集(形成一棵树)
void LinkBSTNode(int nValue ,int lnode, int rnode, int pos);
void FindTPathSum(BSTNode *pRoot, const int exNum, vector<int>& path, int &curNum);
void FindPath(BSTNode *&pRoot, int exceptionNum);
// 节点集
BSTNode *m_pNode;
};
//用前序遍历的方式搜索路劲
void LinkBST::FindTPathSum(BSTNode *pRoot,const int exNum, vector<int>& path, int &curNum)
{
curNum += pRoot->value;
path.push_back(pRoot->count);
//如果pRoot是叶节点,并且路径上节点的值的和等于输入的值
//打印这条路径
bool isLeaf = (pRoot->pLeft == NULL) && (pRoot->pRight == NULL);
if (isLeaf && curNum == exNum)
{
cout << "A path is found: ";
vector<int>::iterator iter = path.begin();
for (; iter != path.end(); iter++)
cout << *iter << " ";
cout << endl;
}
//如果pRoot不是叶节点,则遍历其子节点
if (pRoot->pLeft != NULL)
FindTPathSum(pRoot->pLeft, exNum, path, curNum);
if (pRoot->pRight != NULL)
FindTPathSum(pRoot->pRight, exNum, path, curNum);
//在返回到父节点之前,在路径上删除当前pRoot节点的count
curNum -= pRoot->value;
path.pop_back();
}
void LinkBST::FindPath(BSTNode *&pRoot, int exceptionNum)
{
if (pRoot == NULL)
return;
vector<int> vecpath;
int currentNum = 0;
FindTPathSum(pRoot, exceptionNum, vecpath, currentNum);
}
// 连接节点集(形成一棵树)
void LinkBST::LinkBSTNode(int nValue, int lnode, int rnode, int pos)
{
m_pNode[pos].value = nValue;
m_pNode[pos].count = pos;
if (lnode != -1)
m_pNode[pos].pLeft = &m_pNode[lnode];
if (rnode != -1)
m_pNode[pos].pRight = &m_pNode[rnode];
}
int main()
{
int n = 0, exSum = 0;
while (cin >> n >> exSum)
{
BSTNode *pRoot = NULL;
LinkBST bst(n);
pRoot = &bst.m_pNode[1];//指向根节点
int value = 0, nleftnode = 0, nrightnode = 0;
//插入节点,建立连接
for (int i = 1; i <= n; i++)
{
cin >>value>> nleftnode >> nrightnode;
if (nleftnode>n || nrightnode > n)
exit(1);
bst.LinkBSTNode(value,nleftnode, nrightnode, i);//第i个节点指向第nleftnode个节点和第nrightnode节点
}
cout << "result:" << endl;
bst.FindPath(pRoot,exSum);
}
}
7,二叉排序树
-
题目描述:
-
输入一系列整数,建立二叉排序数,并进行前序,中序,后序遍历。
-
输入:
-
输入第一行包括一个整数n(1<=n<=100)。
接下来的一行包括n个整数。
-
输出:
-
可能有多组测试数据,对于每组数据,将题目所给数据建立一个二叉排序树,并对二叉排序树进行前序、中序和后序遍历。
每种遍历结果输出一行。每行最后一个数据之后有一个空格。
-
样例输入:
-
5 1 6 5 9 8
-
样例输出:
-
1 6 5 9 8 1 5 6 8 9 5 8 9 6 1
-
提示:
-
输入中可能有重复元素,但是输出的二叉树遍历序列中重复元素不用输出。
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
using namespace std;
// 节点定义
class BSTNode
{
public:
BSTNode(int newData )// 默认构造
{
pRight = NULL;
pLeft = NULL;
value = newData;
}
~BSTNode();
friend class LinkBST;// 允许链表类随意访问节点数据
private:
int value;
BSTNode *pRight;
BSTNode *pLeft;
};
// 有头结点的二叉搜索树定义
class LinkBST
{
public:
LinkBST(){
m_pRoot = NULL;
};
~LinkBST(){};
BSTNode* getRoot() const
{
return m_pRoot;
}
// 插入节点
void InsertBTNode(int newData);
// 中序遍历
void inOrder(BSTNode *pRoot);
// 先序遍历
void preOrder(BSTNode *pRoot);
// 后序遍历
void postOrder(BSTNode *pRoot);
private:
BSTNode *m_pRoot;
};
// 中序遍历
void LinkBST::inOrder(BSTNode *pNode)
{
if (pNode != NULL)
{
inOrder(pNode->pLeft);
cout << pNode->value << " ";
inOrder(pNode->pRight);
}
}
// 先序遍历
void LinkBST::preOrder(BSTNode *pNode)
{
if (pNode != NULL)
{
cout << pNode->value << " ";
preOrder(pNode->pLeft);
preOrder(pNode->pRight);
}
}
// 后序遍历
void LinkBST::postOrder(BSTNode *pNode)
{
if (pNode != NULL)
{
postOrder(pNode->pLeft);
postOrder(pNode->pRight);
cout << pNode->value << " ";
}
}
// 插入节点
void LinkBST::InsertBTNode(int newData)
{
BSTNode *newNode = new BSTNode(newData);
if (m_pRoot == NULL)
{
m_pRoot = newNode;
return;
}
BSTNode *pPre = NULL;//用于保存上一个节点
BSTNode *pCur = m_pRoot;
//寻找要插入的节点的位置 (一定是某个叶子)
while (pCur != NULL)
{
pPre = pCur;//保存节点
if (newNode->value < pCur->value)
pCur = pCur->pLeft;//较小值则移到节点的左子树
else if (newNode->value > pCur->value)
pCur = pCur->pRight;
else
break;
}
//建立连接 (不对相等情况进行处理)
if (newNode->value < pPre->value)
pPre->pLeft = newNode;
else if (newNode->value > pPre->value)
pPre->pRight = newNode;
}
int main()
{
int n = 0;
while (cin >> n)
{
LinkBST bst;
int val = 0;
for (int i = 0; i < n; i++)
{
cin >> val;
bst.InsertBTNode(val);
}
bst.preOrder(bst.getRoot());
cout << endl;
bst.inOrder(bst.getRoot());
cout << endl;
bst.postOrder(bst.getRoot());
cout << endl;
}
return 0;
}8,二叉排序树(父节点的值)
-
题目描述:
-
二叉排序树,也称为二叉查找树。可以是一颗空树,也可以是一颗具有如下特性的非空二叉树:
1. 若左子树非空,则左子树上所有节点关键字值均不大于根节点的关键字值;
2. 若右子树非空,则右子树上所有节点关键字值均不小于根节点的关键字值;
3. 左、右子树本身也是一颗二叉排序树。
现在给你N个关键字值各不相同的节点,要求你按顺序插入一个初始为空树的二叉排序树中,每次插入后成功后,求相应的父亲节点的关键字值,如果没有父亲节点,则输出-1。
-
输入:
-
输入包含多组测试数据,每组测试数据两行。
第一行,一个数字N(N<=100),表示待插入的节点数。
第二行,N个互不相同的正整数,表示要顺序插入节点的关键字值,这些值不超过10^8。
-
输出:
-
输出共N行,每次插入节点后,该节点对应的父亲节点的关键字值。
-
样例输入:
-
5 2 5 1 3 4
-
样例输出:
-
-1 2 2 5 3
#include "queue"
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
using namespace std;
// 节点定义
class BSTNode
{
public:
BSTNode(int newData )// 默认构造
{
pRight = NULL;
pLeft = NULL;
pParent = NULL;
value = newData;
}
~BSTNode();
friend class LinkBST;// 允许链表类随意访问节点数据
private:
int value;
BSTNode *pRight;
BSTNode *pLeft;
BSTNode *pParent;
};
// 有头结点的二叉搜索树定义
class LinkBST
{
public:
LinkBST(){
m_pRoot = NULL;
};
~LinkBST(){};
BSTNode* getRoot() const
{
return m_pRoot;
}
// 插入节点
void InsertBTNode(int newData);
private:
BSTNode *m_pRoot;
};
// 插入节点
void LinkBST::InsertBTNode(int newData)
{
BSTNode *newNode = new BSTNode(newData);
if (m_pRoot == NULL)
{
m_pRoot = newNode;
cout << "-1" << endl;
return;
}
BSTNode *pPre = NULL;//用于保存上一个节点
BSTNode *pCur = m_pRoot;
//寻找要插入的节点的位置 (一定是某个叶子)
while (pCur != NULL)
{
pPre = pCur;//保存节点
if (newNode->value < pCur->value)
pCur = pCur->pLeft;//较小值则移到节点的左子树
else if (newNode->value > pCur->value)
pCur = pCur->pRight;
}
//建立连接
if (newNode->value < pPre->value)
pPre->pLeft = newNode;
else if (newNode->value > pPre->value)
pPre->pRight = newNode;
newNode->pParent = pPre;
cout << newNode->pParent->value << endl;
}
int main()
{
int n = 0;
while (cin >> n)
{
LinkBST bst;
int val = 0;
for (int i = 0; i < n; i++)
{
cin >> val;
bst.InsertBTNode(val);
}
}
return 0;
}
/**************************************************************
Problem: 1467
User: EbowTang
Language: C++
Result: Accepted
Time:20 ms
Memory:1520 kb
****************************************************************/
参考资源:
【1】《算法导论》,第二版
【2】《维基百科》
【3】《STL源码剥析》,侯捷著
【4】《C++妙趣横生的算法》,胡浩著
【5】九度OJ,http://ac.jobdu.com/problemset.php?search=二叉树




 本文深入讲解二叉树的概念、设计及实现,包括二叉搜索树的节点与类设计、遍历算法、高度计算等核心内容,并通过多个实例帮助读者理解和应用。
本文深入讲解二叉树的概念、设计及实现,包括二叉搜索树的节点与类设计、遍历算法、高度计算等核心内容,并通过多个实例帮助读者理解和应用。
















 7488
7488

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








