模式识别（Pattern Recognition）学习笔记（十七）--二次判别函数

       前面提到，当概率密度函数满足高斯分布或正态分布的情况，贝叶斯决策的分类面就是一个二次函数，这篇博客来学习有关二次判别。
      首先给出二次判别函数的一般形式：

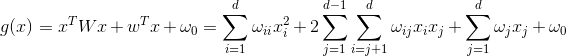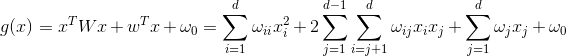             （1）

其中，W是d阶对称方阵，w为d维权向量；

       从判别式中可以看出，有很多参数，其中等式右边第二项就有d(d-1)/2个参数，很明显，这是一个O(n^2)的复杂度，如果仍然像学习线性函数一样去学习这些参数，计算量可想而知会非常大，并且如果样本不足的话就很难保证判别的准确性，当然推广能力也不强，因此在实际解决中，人们往往采用参数估计来估计得到二次判别函数，即估计出每一类的均值和协方差：

假设每一诶样本都满足高斯分布，因此可以定义每一类的判别函数为样本到均值的马氏距离的平方与给定阈值之间的比较：

                  (2)

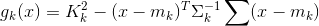
其中，mk为每一样本类的样本均值，∑k是每一类的协方差矩阵，右侧第一项是一个判别阈值，它取决于先验概率和∑k；

均值和协方差的估计：

                          (3)

                    （4）

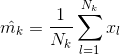
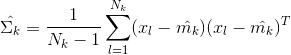
对于一个两类问题，其决策面为：

             (5)

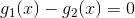
决策规则为：如果左边大于右边，就决策为w1类，右边大于左边，就决策为w2类，如果决策出现错误，可以调整两类的阈值来减小错曲率。

        特殊地，如果其中一类分布比较接近高斯分布，即分布为团状，而另外一类则较均匀的分布在第一类附近，对于这种情况无需作出想公式（5）一样的决策面，只需要求出第一类的判别函数即可，可以看到如公式（2）中，如果第二项（马氏距离平方）小于第一项的阈值，则g(x)>0，于是判为w1类，反之w2类。

       总之，不管需不需要求解决策面方程，都是比较简单的。