设A[1..n]是一个包含N个非负整数的数组。如果在i<j的情况下,有A[i]>A[j],则(i,j)就称为A中的一个逆序对(inversion)。
a)列出数组[2,3,8,6,1]的5个逆序。
b)如果数组的元素取自集合{1,2,...,n},那么,怎样的数组含有最多的逆序对?它包含多少个逆序对?
c)插入排序的运行时间与输入数组中逆序对的数量之间有怎样的关系?说明你的理由。
d)给出一个算法,它能用O(nlogn)的最坏情况运行时间,确定n个元素的任何排列中逆序对的数目(提示:修改归并排序)
——《算法导论》,思考题2-4
问题a)直接根据定义可得<2,1>,<3,1>,<8,6>,<8,1>,<6,1>。
问题b)为了逆序对最多,那么应使任一个数在所有比它小的数前面,从而构成所有可能逆序,即[n,n-1,...,1],这样一共有(n-1)+(n-2) + ... + 1 =n(n-1)/2个。
问题c),在插入排序进行时,数组分为两部分:已排序部分和待排序部分。每次将待排序部分的第一个元素插入到已排序部分时,需要找出其插入的位置,并把这之后的已排序元素依次后移。并且,对于一个元素,插入过程中后移的元素数目就是它在原数组中它前面的逆序对的数目。这是因为,根据逆序对定义,可以写出O(n2)的检测方式,二者是一样的。
for(i=0;j<n;j++)
for(i=0;i<j;i++)
if(A[i]>A[j])
count++;1.在归并排序中,同样是对一个数组分为两段处理,在处理这两段时,并不会影响右段元素与左段元素的逆序关系,只有在归并时才会改变。
2.归并时的改变方式和插入排序是类似的:右段中取出元素放在左段其余所有元素前面时,相当于左段整体后移,后移的元素数就是这个逆序数。
3.由于归并排序使用的是分治法,将每次归并的逆序数累加,最后结果就是总的逆序数。并且,归并排序的时间复杂度是O(nlogn),优于插入排序。
给出一个算法,它能用O(n lgn)的最坏情况运行时间,确定n个不同元素的任何排列中逆序对的数目。
答:解决这个问题的核心问题是一个排列的逆序对数等于分解的二个排列的逆序对数加上二个排列之间的逆序对数之和。
即:将一个个数为n的排列分解为个数为m1和m2二个排列,证明
接着就是利用递归算法的从底层向上运算的特性逐层求解各层的逆序对数。
问题化简成如何求解二个有序排列的逆序对数了;
解:
将A排列分解成B和C二个有序排列;i为B中的数,j为C中数;在合并排序时,i<j则将j放回A中;
也就是说,设C中已有b个数放入A中;针对i有b个逆序对;最后将B中所有数的逆序对数相加,
即可求出二个排列之间的逆序对数。
public class Solution {
public int InversePairs(int [] array) {
// Can solve by using divide and conquer
if(array == null){
return 0;
}
int len = array.length;
return InversePairs(array,0,len-1);
}
private int InversePairs(int[] array, int start, int end){
if(start >= end){
return 0;
}
int mid = (start + end) / 2;
int leftPairs = InversePairs(array,start,mid);
int rightPairs = InversePairs(array,mid+1,end);
int leftRightPairs = mergePairs(array,start,mid,end);
return leftPairs + rightPairs + leftRightPairs;
}
private int mergePairs(int[] array,int start,int mid,int end){
int[] tmp = new int[end - start + 1];
int i = start;
int j = mid + 1;
int k = 0;
int count = 0;
while(i <= mid && j <= end){
if(array[i] > array[j]){
count += (end - j + 1);
tmp[k++] = array[i++];
}else{
tmp[k++] = array[j++];
}
}
while(i <= mid){
tmp[k++] = array[i++];
}
while(j <= end){
tmp[k++] = array[j++];
}
k = 0;
for(int m = start;m<=end;m++){
array[m] = tmp[k++];
}
return count;
}
}








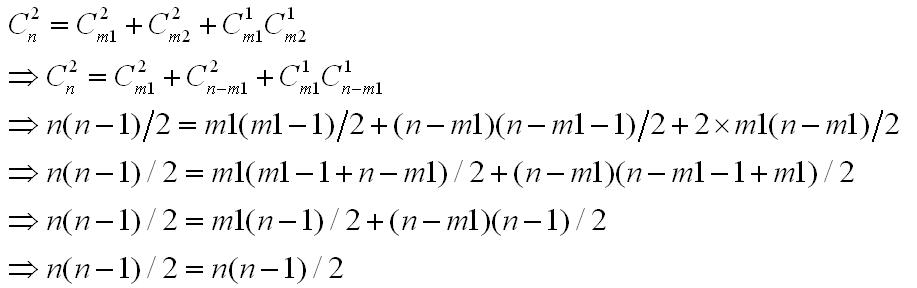













 556
556











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








