数的划分

问题描述

将整数n分成k份，且每份不能为空，任意两种分法不能相同（不考虑顺序）。
例如：n=7,k=3,下面三种分法被认为是相同的：
1，1，5； 1，5，1； 5，1，1。
问有多少种不同的分法。
输入：n,k(6<n<=200,2<=k<=6)
输出：一个整数，即不同的分法。

输入输出样例

输入：
7 3
输出：
4

问题分析：

这是一道整数剖分的问题。这类问题的数学性很强，方法也很多。

首先，正确理解“整数n分成k份，这k个整数不考虑顺序的含义”指的是同一种划分与k个整数的排列无关，例如下面5种8的4划分看作是同一种划分法：

1＋2＋2＋3；2＋2＋3＋1； 1＋3＋2＋2；3＋2＋1＋2 ；2＋2＋1＋3。

因此将n划分份的一种方法唯一的表示为n1+n2+……nk,其中n1<=n2<=….nk.

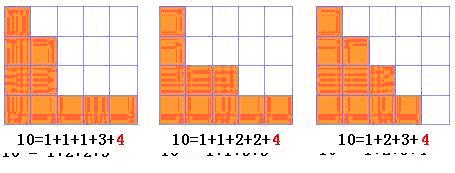
       这样可以形象地把n的k份划分看作是把n块积木堆成k列，且每列的积木块数依次递增，也就是这n块积木从左到右被堆成了“阶梯状”。比如，下图是10的几种划分方法：

把上图的三个矩形顺时针旋转90度后，如下图：

不难发现，选转之后的模型还是10的划分，不过约束条件有所不同。很明显，由于原来是k份划分，因此新的模型中的最大一个元素必然是k。而其余的元素大小不限，但都不能大于k.  n减去k后，n’=n-k, 剩下的问题就是求n’的任意划分，且其中每个元素都不大于k的方案总数了。

       新模型中，n的k份剖分的一种分法表示为n块积木从右到左递增排列，其中最左列有k块积木。

       两个模型中对n的k份剖分的每种分法表示是一一对应的，如：

10＝1＋2＋2＋5      对应    10＝4＋3＋1＋1＋1

       10＝1＋1＋3＋5      对应    10＝4＋2＋2＋1＋1

       10＝1＋2＋3＋4      对应    10＝4＋3＋2＋1

       因此，求n的k份划分的方案总数问题转化为根据新模型将n做任意划分，且其中最大的一个部分恰好是k的问题。

       求解这个新的模型可以用递推的方法，用f (a,b)表示把b做任意份剖分，其中最大的一个部分等于a的方案总数，用g(a,b)表示把b做任意份划分，其中最大的一个部分不大于a的方案总数，则有：

       f (a,b)=g (a,b-a);

       g(a,b)＝f(1,b)+f(2,b)+...f(a,b);

因为：

f(1,b)+f(2,b)+...f(a,b) =f(1,b)+...f(i,b)  +f(a,b) (1<=i<=a-1)

f(1,b)+f(2,b)+..f(a-1,b) =g(a-1,b)

所以:

g(a,b)=f(1,b)+...f(i,b)＋f(a,b)=g(a-1,b)+g(a,b-a)(1<=i<=a-1)

当b<a时，根据g(a,b)的含义，g(a,b-a)无意义。

当a=1时，显然 g(1,b)=1.

于是，根据新模型求解得到下列递推公式：

  g (a,b)=   g (a-1,b） b<a

            g (a-1,b)+g(a,b-a) b>=a.

g(1,b)=1.

最后的g (k,n-k)即为所求。

参考程序：

#include<iostream>
#include<cstring>
using namespace std;
int g[7][201];
int main()
 {   freopen("in.txt","r",stdin);
     freopen("out.txt","w",stdout);
     int n,k,i,j;
     while(cin>>n>>k)
      {
          memset(g,0,sizeof(g));
          for(j=0;j<=n;j++)
           g[1][j]=1;
          for(i=2;i<=k;i++)
           for(j=0;j<=n-k;j++)
            if(j>=i)
              g[i][j]=g[i-1][j]+g[i][j-i];
            else
              g[i][j]=g[i-1][j];
       cout<<g[k][n-k]<<endl;        
      }   
    
     return 0;
 }