Codeforces Round #369 (Div. 2) [D] Directed Roads

Directed Roads

time limit per test:2 seconds

memory limit per test:256 megabytes

input:standard input

output:standard output

ZS the Coder and Chris the Baboon has explored Udayland for quite some time. They realize that it consists of n towns numbered from 1 to n.

There are n directed roads in the Udayland. i-th of them goes from town i to some other town a_i (a_i ≠ i). ZS the Coder can flip the direction of any road in Udayland, i.e. if it goes from town A to town B before the flip, it will go from town B to town A after.

ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns A₁, A₂, ..., A_k (k > 1) such that for every 1 ≤ i < k there is a road from town A_i to town A_i + 1 and another road from town A_k to town A₁. In other words, the roads are confusing if some of them form a directed cycle of some towns.

Now ZS the Coder wonders how many sets of roads (there are 2ⁿ variants) in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.

Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.

Input

The first line of the input contains single integer n (2 ≤ n ≤ 2·10⁵) — the number of towns in Udayland.

The next line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ n, a_i ≠ i), a_i denotes a road going from town i to town a_i.

Output

Print a single integer — the number of ways to flip some set of the roads so that the resulting whole set of all roads is not confusing. Since this number may be too large, print the answer modulo 10⁹ + 7.

Examples

Input

3
2 3 1

Output

6

Input

4
2 1 1 1

Output

8

Input

5
2 4 2 5 3

Output

28

Note

Consider the first sample case. There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are 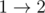, , 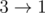initially. Number the roads 1 to 3 in this order.

The sets of roads that ZS the Coder can flip (to make them not confusing) are {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Note that the empty set is invalid because if no roads are flipped, then towns 1, 2, 3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.

The sample image shows all possible ways of orienting the roads from the first sample such that the network is not confusing.

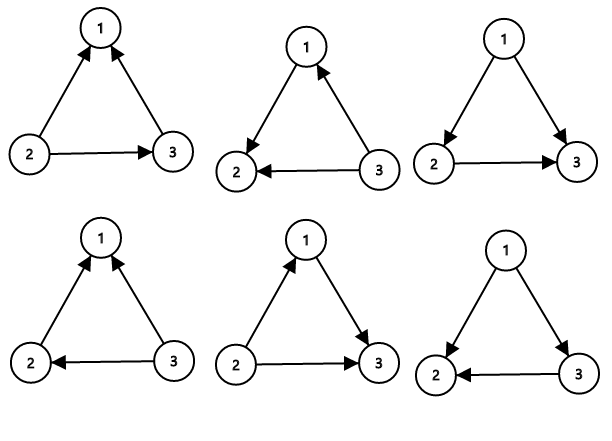
题意:给你一个n个点，n条有向边的图，你可以使任意条边反向，但是每条边只能反向一次，请求出使图不存在环的所有方案数量

仔细思考我们发现，对于一个点数为x的环，除去全部不反向和全部反向两种情况，其他的所有方案总数为(2^x)-2种

对于不在环上的边，无论反向还是不反向对环的存在都是没有影响的，因此如果有y条边不在环上，就有2^y种情况

最后将所有的情况乘起来就可以了，环的存在需要dfs预处理一下

#include<cstdio>
#include<iostream>
#define LL long long
using namespace std;
const LL maxn=2e5+5;
const LL mod=1e9+7;
LL n,NEXT[maxn],vis[maxn],tot,loops[maxn];
inline void _read(LL &x){
    char t=getchar();bool sign=true;
    while(t<'0'||t>'9')
    {if(t=='-')sign=false;t=getchar();}
    for(x=0;t>='0'&&t<='9';t=getchar())x=x*10+t-'0';
    if(!sign)x=-x;
}
LL mg(LL a,LL b,LL c){
    LL ans=1;
    a%=c;
    while(b){
        if(b&1)ans=(ans*a)%c;
        b>>=1;
        a=(a*a)%c;
    }
    return ans;
}
void find_loops(LL x){
	loops[tot]++;
	vis[x]=3;
	if(vis[NEXT[x]]==3)return ;
	find_loops(NEXT[x]);
}
void dfs(LL x){
	vis[x]=2;
	if(!vis[NEXT[x]])dfs(NEXT[x]);
	if(vis[NEXT[x]]==2){
		tot++;
		find_loops(x);
	}
	if(vis[NEXT[x]]==1||vis[NEXT[x]]==3)vis[x]=1;
}
int main(){
	LL i,ans=1;
	_read(n);
	for(i=1;i<=n;i++)_read(NEXT[i]);
	for(i=1;i<=n;i++)
	    if(!vis[i])dfs(i);
	for(i=1;i<=tot;i++)ans=ans*(mg(2,loops[i],mod)-2+mod)%mod,n-=loops[i];
	cout<<ans*mg(2,n,mod)%mod;
}