循环赛日程表问题

最近在学习算法分析与设计这门课时，遇到了循环赛日程表问题。我感觉课本上的方法并不是很好(浪费空间而又不好理解)，而网上流传的代码也基本和课本上类似，于是我决定用自己的方式来实现这个算法。

目录

问题描述

设有n=2^k个运动员要进行羽毛球循环赛，现要设计一个满足以下要求的比赛日程表：

1. 每个选手必须与其他n-1个选手各赛一次；
2. 每个选手一天只能赛一次；
3. 循环赛一共需要进行n-1天
   由于n=2^k，显然n为偶数。

算法思路

根据分治法的思想，递归地将问题一分为二，直到只剩下两个人比赛，最后在将这些问题合并起来，这样问题就变得十分简单。日程表的制定过程中存在一定的规律，即第i行第j列表示第i个选手在第j天所遇到的选手。这样算法就很容易实现了。

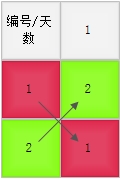
2^1个选手的比赛日程表

当问题规模为2^1时，此时问题最为简单，只需要将每个选手复制到对角线位置即可。

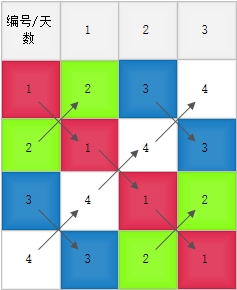
2^2个选手的比赛日程表

当问题规模为2^2时，将问题划分为2个规模为2^1的子问题，先解决子问题，然后在将问题规模为2^1的子问题看作一个整体，并复制到对角线位置，这时即可得到总问题的解。

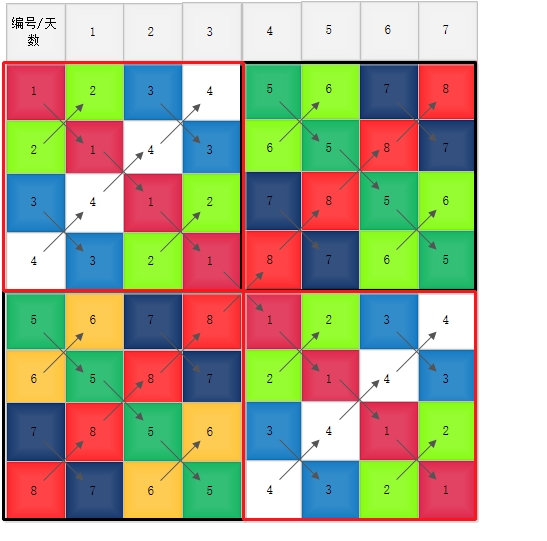
2^3个选手的比赛日程表

与上面类似，先将问题划分为4个问题规模为2^1的子问题，分别解决后，再将这些子问题看作一个整体分别复制到对角线处，即可得到两个问题规模为2^2的子问题，最后再将规模变大了的子问题分别复制到对角线处，即可得到总问题的解。

……

算法实现

这里我只对代码的关键部分做简要的解释，即下面部分：

#define N 3
...
int sche = pow(2.0, N);      // divide the problem to pow(2, k) subproblems
...

for (int j = 0; j < N; j++)
    {
        // gets the size of the problem,
        // every loop the problem will triple
        bw = pow(2.0, j);
        for (int r = 0; r < bw; r++)
        {
            for (int c = 0; c < sche; c++)
            {
                // uses round to get the index of problem block
                bid = (c + bw) / bw;
                c_offset = pow(-1.0, bid + 1) * bw;
                r_offset = bw;
                arr[r + r_offset][c + c_offset] = arr[r][c];
            }
        }
    }

代码中使用了三层循环，最外层的循环控制问题的规模，即当j=0时，问题规模最小，即前面介绍的规模为2^1的问题；当j=1时，问题规模为2^2；当j=2时，问题规模为2^3……以此类推。这部分可以最能体现分治法的特点，将大问题划分为小问题。

第二层与第三层分别控制元素的行和列，这两层循环主要负责解决不同规模的问题，简单地说就是分别将不同规模的问题块复制到对角线的位置。

为了完成这个看似简单的过程，我们首先需要找一下规律(由于2^k必为偶数，所以n为奇数)：

• 子问题规模为2^1(j=0)时，

a[0][0]–>a[1][1]

a[0][1]–>a[1][0]

a[0][2]–>a[1][3]

a[0][3]–>a[1][2]

…

a[0][n-1]–>a[0+2^0][(n-1)+2^0]

a[0][n]–>a[0+2^0][n-2^0]

也就是说当元素的ID(ID=列号+1)为奇数时，移动到右下角(横纵坐标分别加2^0)；当列ID为偶数时，移动到左下角(横坐标减2^0，纵坐标加2^0)。

• 子问题规模为2^2(j=1)时，

a[0][0]–>a[2][2]

a[0][1]–>a[2][3]

a[0][2]–>a[2][0]

a[0][3]–>a[2][1]

…

a[0][n-3]–>a[0][(n-3)+2^1]

a[0][n-2]–>a[0][(n-2)+2^1]

a[0][n-1]–>a[0+2^1][(n-1)-2^1]

a[0][n]–>a[0+2^1][n-2^1]

现在规律就没有那么明显了，但是如果我们按照整块来找规律的话，那么规律就相对容易找一些。你可以这样划分块：即按照2x2的块来划分，每个块都对应一个ID，同样当ID为奇数时，移动到右下角(横纵坐标分别加2^1)；当ID为偶数时，移动到左下角(横坐标减2^1，纵坐标加2^1)。

NOTE:其实问题规模为2^1时，块的大小为1x1。

• 当子问题规模为2^3(j=2)时，

a[0][0]–>a[4][4]

…

a[0][2]–>a[4][6]

…

a[0][4]–>a[4][0]

…

a[0][7]–>a[4][3]

很显然，这里块的大小为4x4，移动的方法我这里也就不在赘述了。

综上所述，块的大小分别是2^0x2^0，2^1x2^1，2^2x2^x,…,2^nx2^n，每次都按照块来进行对角线复制，这时规律就显而易见了，所以r(行ID)的最大值就是块的宽度。但是还有一个比较棘手的问题——如何将数组中的每个元素与块的ID一一映射呢？我经过一番思考终于找到了规律：

BLOCK_ID = (COL_ID + BLOCK_WIDTH)/BLOCK_WIDTH

原代码中是这样写的:

  bid = (c + bw) / bw;

其实上面这个式子的灵感来源于我最近在学的CUDA编程中一个经典例子，在那里我学到了圆整(rounding)这个概念(实际上很早就接触过这个东西，只是当时并没有这个概念)，圆整的方式有很多，常见的就有向上圆整(round up)和向下圆整(round down)，如果你对圆整感兴趣，可以参考相关词条rounding。在我的这个式子中就用到了向上取整的方式，很容易理解，这里就不在赘述了。

到这里，所有的问题都解决了。

NOTE:细心的朋友可能会注意到，源码中是按行复制的。这与图中按列复制并不一致，但原理是一样的。

你可以在这里下载源码。

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。