强连通图的‘太监’算法（tarjan）-两种方式



有向图强连通分量的Tarjan算法 [有向图强连通分量]

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

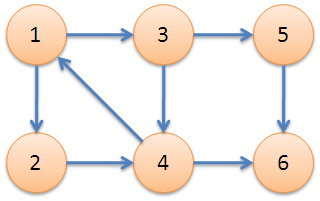
直接根据定义，用双向遍历取交集的方法求强连通分量，时间复杂度为O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法，两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。 [Tarjan算法]

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出，

Low(u)=Min
{
   DFN(u),
   Low(v),(u,v)为树枝边，u为v的父节点
   DFN(v),(u,v)为指向栈中节点的后向边(非横叉边)
}

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

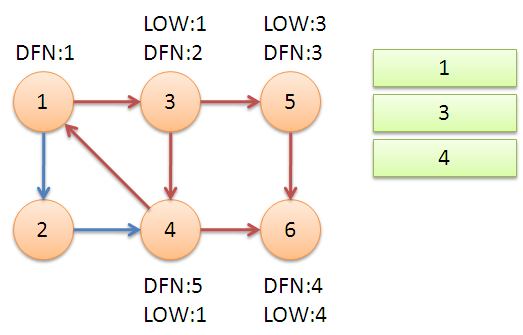
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

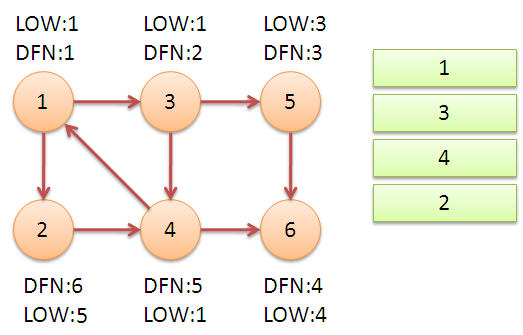
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

求有向图的强连通分量还有一个强有力的算法，为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法，其时间复杂度也是 O(N+M)。与Trajan算法相比，Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS，不用建立逆图，更简洁。在实际的测试中，Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外，该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法，也有助于深入理解求双连通分量的Tarjan算法，两者可以类比、组合理解。

求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法，以及求最近公共祖先的离线Tarjan算法，在此对Tarjan表示崇高的敬意。

附：tarjan算法的C++程序

模板1：

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<limits.h>
#include<stdlib.h>
#include<math.h>
#include<queue>
#include<map>
#define maxn 10005
using namespace std;
struct Edge
{
	int v;
	int next;
}edge[maxn];
int node[maxn];//顶点集合
int instack[maxn];//标记是否在栈中
int stack[maxn];
int belong[maxn];//各顶点属于哪个强连通分量
int dfn[maxn];//节点u搜索的序号（时间戳）
int low[maxn];//u或u的子树能够追溯到的最早的栈中节点的序号
int n,m;//n:点的个数,m:边的个数
int cnt;//记录边数
int time;//序号
int top;
int sum;//有多少个强连通分量
build(int u,int v)//建立邻接表
{
	edge[cnt].next=node[u];
	edge[cnt].v=v;
	node[u]=cnt++; 
} 
void tarjan(int u)
{
	int i,j;
	int v;
	dfn[u]=low[u]=++time;
	instack[u]=1;
	stack[++top]=u;
	for(i=node[u];i!=-1;i=edge[i].next)
	{
		v=edge[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			if(low[v]>low[u])
			  low[v]=low[u];
		}
		else
		  if(instack[v] && dfn[v]<low[u])
		    low[u]=dfn[v];
	}
	if(dfn[u]==low[u])
	{
	   sum++;
	   do//不管while里的条件真假都要先执行一次 
	   {
	   	   j=stack[top--];
	   	   instack[j]=0;
	   	   belong[j]=sum;
	   }while(j!=u);
    }
}
void solve()
{
	int i;
	top=sum=time=0;
	memset(dfn,0,sizeof(dfn));

        memset(instack,0,sizeof(instack));

        memset(stack,0,sizeof(stack));
	memset(low,0,sizeof(low));
	for(i=1;i<=n;i++)
	   if(!dfn[i])
	      tarjan(i); 
 } 
 int  main()
 {
 	int i,j,k;
	 cnt=0; 
	memset(node,-1,sizeof(node));
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++)
	  {
	  	scanf("%d%d",&j,&k);
	  	build(j,k);
	  }
	  solve();
	  for(i=1;i<=n;i++)
	     printf("%d ",belong[i]); 
 } 

模板2：

1 #include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <stack>
#define max(a,b) (a>b?a:b)
#define min(a,b) (a>b?b:a)
using namespace std;

const int N=1001;
int time=1;
int low[N],dfn[N];
bool instack[N];
stack<int>st;

struct LIST
{
    int v;
    LIST *next;
};
LIST *head[N]={NULL};

void tarjan(int v)/*tarjan求强连通分支*/
{
    dfn[v]=low[v]=time++;/*标记点v的DFS遍历序号*/
    st.push(v);/*将点v入栈*/
    instack[v]=true;/*标记点v已经在栈中*/
    for(LIST *p=head[v];p!=NULL;p=p->next)/*遍历V能直接到达的点*/
    {
        if(!dfn[p->v])/*如果v的邻接点没有入过栈*/
        {
            tarjan(p->v);
            low[v]=min(low[v],low[p->v]);/*如果v能直接到达的这个点没在栈中,v的最早祖先为他们中的较小值*/
        }
        else if(instack[p->v])/*如果在栈中*/
            low[v]=min(low[v],dfn[p->v]);/*如果在栈中，则v的最早祖先是他的序号和那个点的序号较小的*/
    }
    if(dfn[v]==low[v])/*如果dfn[v]和low[v]相等，则说明v点是其所属强连通分支DFS遍历起点，这个强连通分支所有点都在v点之上*/
    {
        cout<<"{ ";
        do
        {
            v=st.top();
            st.pop();
            instack[v]=false;
            cout<<v<<' ';
        }while(dfn[v]!=low[v]);
        cout<<"}"<<endl;        
    }
}

int main()
{
    int i,j,n,m;
    cin>>n;
    while(!st.empty())
        st.pop();
    memset(dfn,0,sizeof(dfn));
    memset(instack,false,sizeof(instack));
    for(i=0;i<=n;i++)
        head[i]=NULL;
    for(i=1;i<=n;i++)
    {            
        cin>>m;//i的邻接点数量
        //输入每个邻接点编号
        LIST *rear=head[i];
        for(j=0;j<m;j++)/*创建邻接表*/
        {
            if(!j)
            {
                rear=new LIST;
                head[i]=rear;
            }
            else
            {
                rear->next=new LIST;
                rear=rear->next;
            }
            rear->next=NULL;
            cin>>rear->v;
        }
    }
    for(i=1;i<=n;i++)
        if(!dfn[i])/*如果i没有入过栈*/
            tarjan(i);
    return 0;
}
88